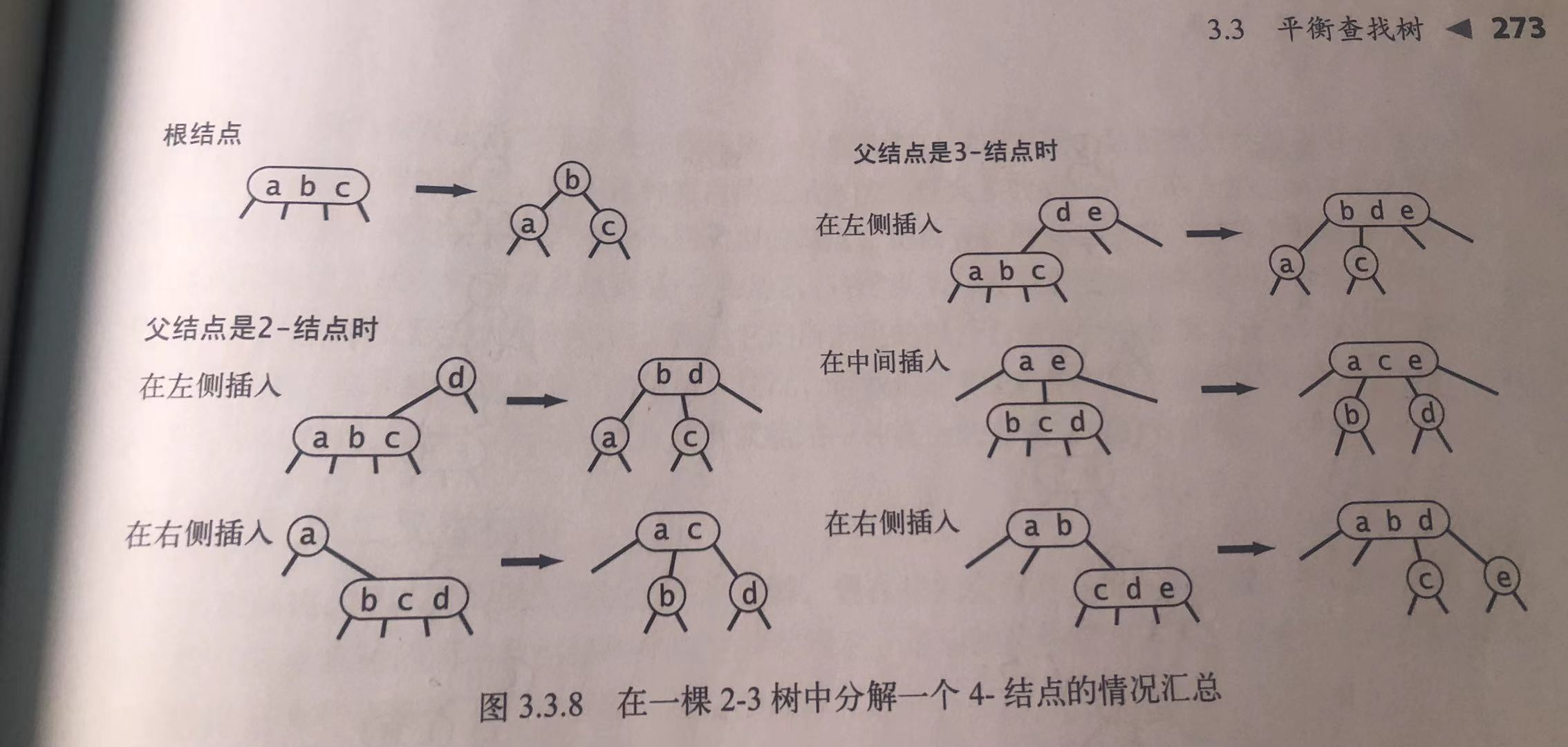
2-3查找树

本质是一颗二叉查找树,分别有2种节点:
(1)2节点:含有一个键和两条连接(左连接都小于键,右连接都大于键)
(2)3节点:含有两个键和三条连接(左连接都小于两个键,中连接值位于两个键之间的,右连接大于键)
这里注意:2、3针对的是连接的数量 而不是键值的数量
完美平衡2-3查找树:所有空连接到根结点的距离相同。
一、查找
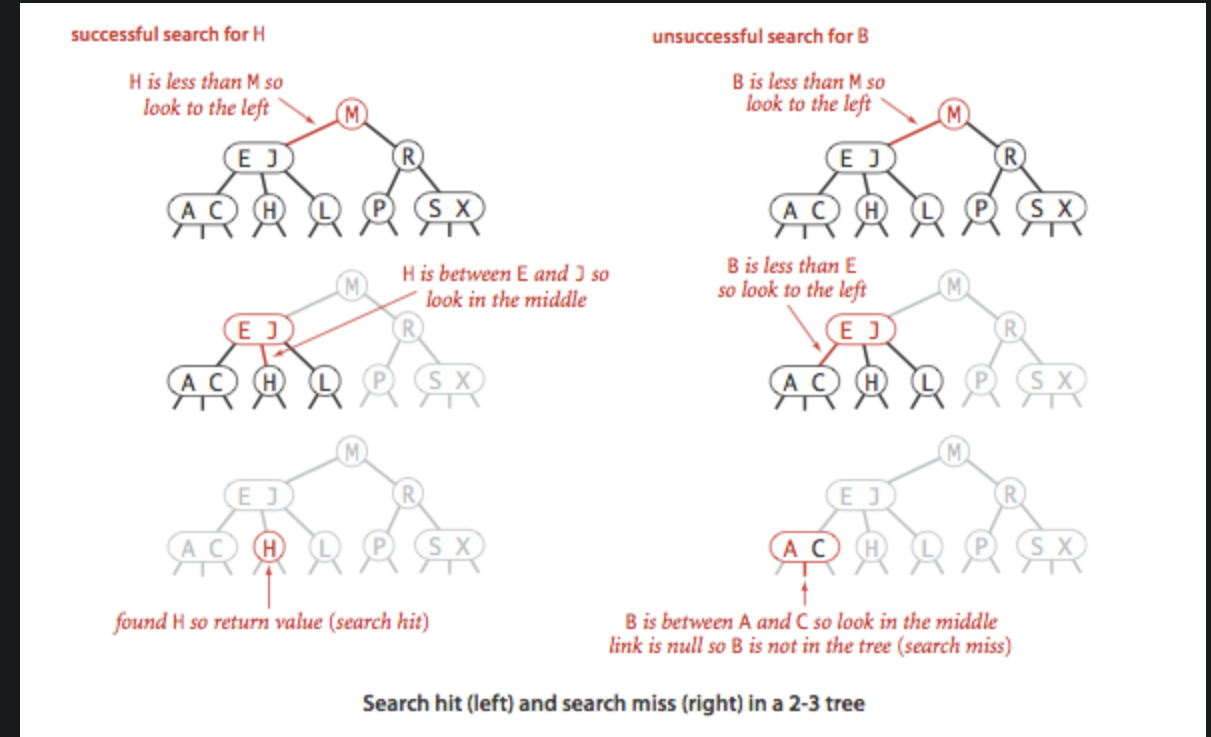
(1)判断和根节点键是否一致,如果和任意一个相等,则命中
(2)如果不相等,根据比较的结果去到相应的区间
(3)在相应的子树进行递归查找,如果子树为空连接则查找失败。
二、向2节点插入(结束的节点为2节点)

如果我们想在上图树中插入K,先查找,结果是未命中,所以要进行插入。
(1)将2节点替换为一个3节点
三、向只有一个3节点插入(只有一个节点不明白吗,就是这个树 只有一个节点 就是一个3节点)
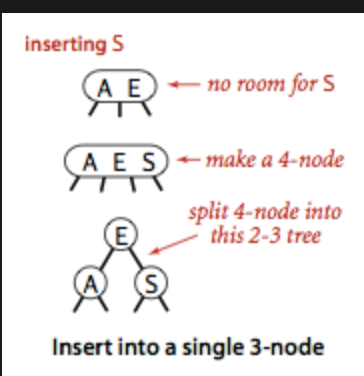
(1)先将新键插入3节点,生成一个4节点(再次重申:4节点对应的是3个键 4条连接)
(2)将4节点化为3个2节点
(3)结果还是平衡的(原来完美平衡二叉树,空连接到根节点为n,现在为n+1)
(平衡的意思是:任意节点的子树的高度差都小于等于1)
四、向一个3节点插入,父节点为2节点
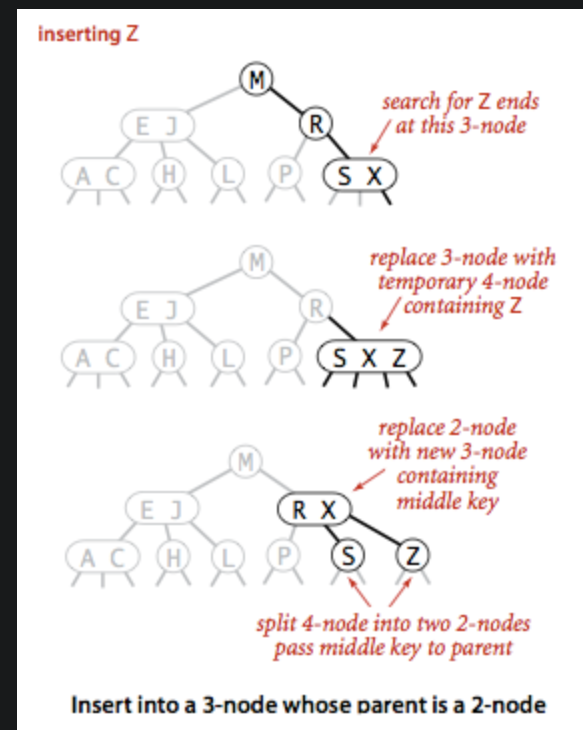
(1)创造一个临时4节点
(2)将4节点的中键移入父2节点里(为什么是中键,上图例子:X上去 组成(R,X)2节点 才能出现,S在(R,X)中间连接,Z在右连接,反向同理)
(3)完成插入,依旧平衡且有序
五、向一个3节点插入,其父节点为3节点
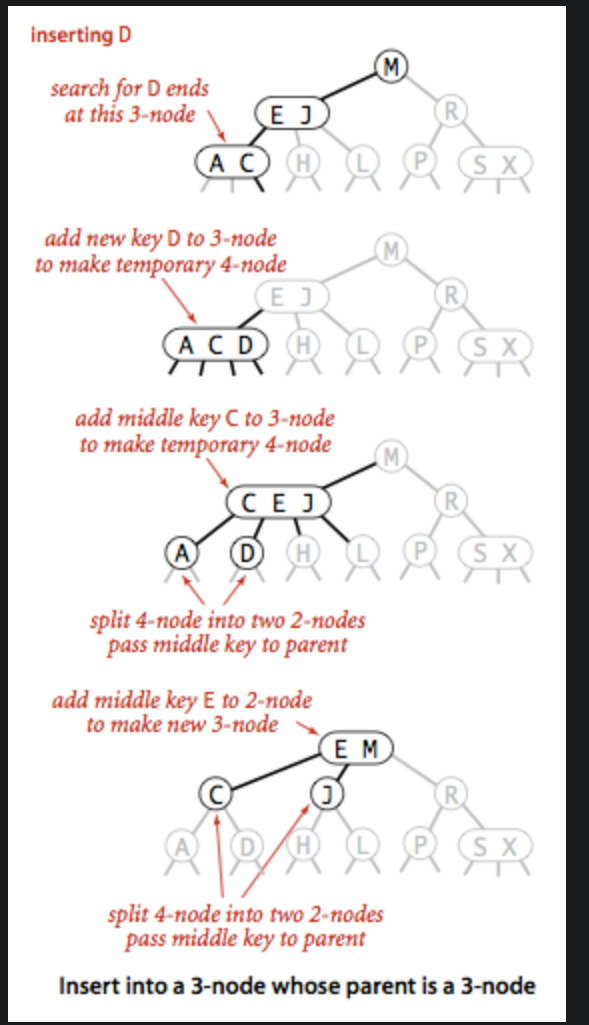
(1)创建临时4节点 (A,C,D)
(2)将中键C传给父3节点
(3)父3节点(E,J)依旧创建临时4节点(C,E,J)
(4)将中键E上传
。。。。。
(n)直到遇到一个2节点,将他变为3节点
或
(n)根节点也为3节点,就应用 本文的第三个方法 将3节点变为2节点
六、将一个4节点分解到一个2-3查找树的6种情况