Bezier画线算法

编译器：VS2013

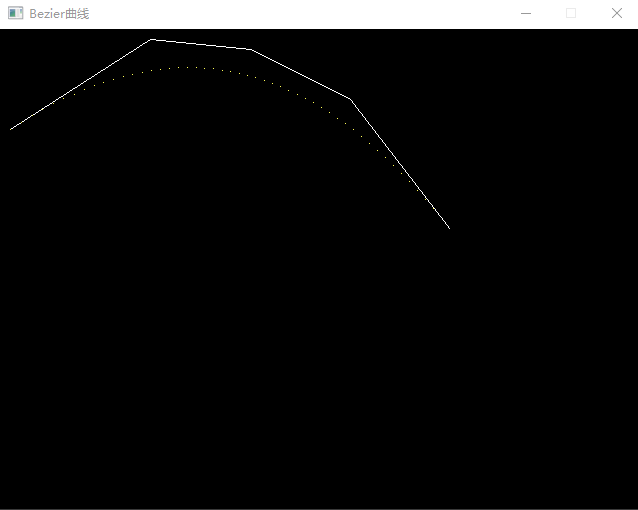
描述：Bezier画线是利用导数相同拼接曲线，使曲线十分光滑，而不是随意拼接观赏性很差

主函数段

#include "stdafx.h"
#include<stdio.h>
#include"graphics.h"
#include<stdlib.h>
#include<math.h>

//函数声明
void Bezier4(int a[]);//四个控制点画出曲线
void Beziern(int a[], int N);//N个点画出曲线
int factorial(int n);//利用递归求出阶乘

int main()
{
    int *p, N,gdriver = DETECT, gmove, i;

    printf("please input the number of point
");
    scanf_s("%d", &N);

    p = (int *)malloc(2 * N*sizeof(int));

    printf("please input the coordinate:
");
    for (i = 0; i < 2 * N; i += 2)
        scanf_s("%d%d", &p[i], &p[i + 1]);

    initgraph(&gdriver, &gmove, "");

    //画出多边形
    for (i = 0; i < 2*N-2; i += 2)
        line(p[i], p[i + 1], p[i + 2], p[i + 3]);

    Beziern(p, N);

    system("pause");

    closegraph();

    return 0;
}

Bezier画线函数

//N个点画出曲线
void Beziern(int a[], int N)
{
    double t, X1 = a[0], Y1 = a[1];
    int k,i;

    for (t = 0; t <= 1; t += 0.02)
    {
        putpixel(X1, Y1, YELLOW);

        X1 = 0, Y1 = 0;

        for (i=0,k = 0; k<N; i+=2,k ++)
        {
            X1 += 1.0*a[i] * factorial(N-1) / factorial(k) / factorial(N-1 - k)*pow(t, k)*pow(1 - t, N-1 - k);//pow函数为求指数的函数
            Y1 += 1.0*a[i+1] * factorial(N-1) / factorial(k) / factorial(N-1 - k)*pow(t, k)*pow(1 - t, N -1- k);
        }

    }
}

//利用递归求出阶乘
inline int factorial(int n)
{
    if (n > 1)
        return n*factorial(n - 1);
    else
        return 1;
}

结果：