[LeetCode]287. Find the Duplicate Number

Medium

Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.

There is only one duplicate number in nums, return this duplicate number.

Follow-ups:

1. How can we prove that at least one duplicate number must exist in nums? 
2. Can you solve the problem without modifying the array nums?
3. Can you solve the problem using only constant, O(1) extra space?
4. Can you solve the problem with runtime complexity less than O(n2)?

Example 1:

Input: nums = [1,3,4,2,2]
Output: 2

Example 2:

Input: nums = [3,1,3,4,2]
Output: 3

Example 3:

Input: nums = [1,1]
Output: 1

Example 4:

Input: nums = [1,1,2]
Output: 1

Constraints:

• 2 <= n <= 3 * 104
• nums.length == n + 1
• 1 <= nums[i] <= n
• All the integers in nums appear only once except for precisely one integer which appears two or more times.

题目大意：

长度为n+1的数组中，存放这1-n之间的整数，有且只有一个数字发生重复，找出这个重复的数字。

要求：

1.空间复杂度为O(1)

2.时间复杂度小于O(n^2)

3.不能重构这个数组

方法

题目的三个要求分别排除了：

1.使用hashMap或数组进行数字的出现次数统计

2.双层遍历，暴力求解

3.对数组进行有序排列，再一次遍历求解

参考网上的解析，有以下几种方法。

方法一：

二分求解。因为时间复杂度要求小于O(n^2)，所以外层循环采用二分法的方式，内层仍为遍历，这样时间复杂度变为O(n*log(n))。内层遍历数组统计小于mid的数字个数，如果比mid小，就说明重复的那个数字比mid大，否则比mid小，然后移动左右游标，进一步缩小搜索范围。

注意：这里的left、right和mid，都可以看作是在有序数组1-n上移动的游标，而不是在当前的数组上移动的游标。

代码如下：

/*** C++ ***/
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int left = 1, right = nums.size();
        while(left<right){
            int mid = left+(right-left)/2,cnt=0;
            for(int num:nums){
                if(num<=mid)++cnt;
            }
            if(cnt<=mid)left=mid+1;
            else right=mid;
        }
        return right;
    }
};

 Python3

#Python3
class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        left = 1
        right = len(nums)
        while left < right :
            mid = left+(right-left)/2
            cnt=0
            for num in nums :
                if num <= mid:
                    cnt=cnt+1
            if cnt<=mid:
                left = mid+1
            else:
                right=mid
        return int(right)

方法二：

使用快慢指针，因为存在重复数字，那么必然会行程闭环，即每次遇到那个重复的数字x，我们都会被扔进一样的数字序列中。第一步，使用快慢指针，让游标进入圈子中，第二步，让一个新的游标从0开始出发，圈子内的游标和圈子外的游标同步移动，直到外部的游标进入圈子，即遇到重复数字，这时圈子内的游标也恰好会遇到重复数字，此时游标对应的值就是那个重复数字。

（证明快慢指针相遇时，0到圈子初始的步数=slow到圈子重复点的步数，下边是一个不严谨证明，仅供理解代码思路）

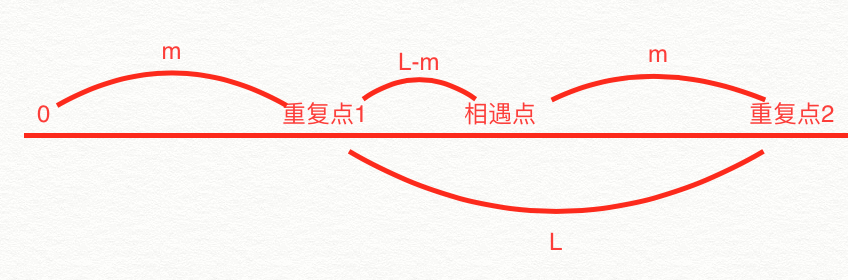
我们可以把游标的移动看作是在一串固定数字串上进行移动，设0->圈子的步数是m，圈子周长为L，快慢指针相遇时，快指针走过的步数一定是慢指针的2倍，那么假设相遇时距离圈子开端的步数是x，那么可以得到式子m+L+x=2*(m+x)，计算得出x=L-m，也就是说相遇时慢指针距离重复点的步数恰好是0到重复点的步数。因此在相遇后从0出发的点一定会在重复点与慢指针相遇。

代码如下：

C++

/*** C++ ***/
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast=0, slow=0, t=0;
        while(true){
            slow = nums[slow];
            fast = nums[nums[fast]];
            if(slow==fast)break;
        }
        while(true){
            slow=nums[slow];
            t=nums[t];
            if(t==slow)break;
        }
        return slow;
    }
};

 JavaScript

// JavaScript
var findDuplicate = function(nums) {
    let slow=0,fast=0,t=0;
    while(true){
        slow=nums[slow];
        fast=nums[nums[fast]];
        if(fast==slow)break;
    }
    while(true){
        slow=nums[slow];
        t=nums[t];
        if(slow==t)break;
    }
    return slow;
};

 Python3

# Python3
class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        slow = 0 
        fast = 0
        t = 0
        while True :
            slow = nums[slow]
            fast = nums[nums[fast]]
            if fast == slow :
                break
        while True :
            slow = nums[slow]
            t = nums[t]
            if t == slow :
                break
        return slow

 方法三

使用二进制移位的方式进行计数。因为1 ~ (n-1)的所有数字，每一位上出现的1的个数是一定的，遍历数组中的每个数字，当某一位上的1较多时，这个多出来的'1'就是那个重复数字的'1'，把这些1拼起来就是那个重复数字了。因为数组长度是n+1，数组索引值是0~n，所以可以在1次遍历中完成1位数字的统计。

代码如下：

/*** C++ ***/
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int res=0;
        for(int i=0;i<32;++i){
            int bit=(1<<i), cnt1=0, cnt2=0;
            for(int k=0;k<nums.size();++k){
                if((k&bit)>0)cnt1++;
                if((nums[k]&bit)>0)cnt2++;
            }
            if(cnt2>cnt1)res+=bit;
        }
        return res;
    }
};