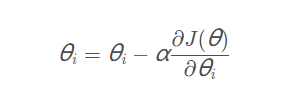逻辑回归

逻辑回归

一、什么是逻辑回归

是用于处理因变量为分类变量的回归问题，常见的是二分类或二项分布问题，也可以处理多分类问题，它实际上是属于一种分类方法。主要思想是用最大似然概率方法构造方差，为最大化方差，利用牛顿梯度上升求解方差参数。

优缺点如下：

优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。
使用数据类型：数值型和标称型数据。
4.样本特征是相互独立

二、逻辑回归的推导

首先来看一下最大似然概率的思想：

有个黑箱，里面有白球和黑球。我们从里面抓3个球，2个黑球，1个白球。这时候，有人就直接得出了黑球67%，白球占比33%。这个时候，
其实这个人使用了最大似然概率的思想，通俗来讲，当黑球是67%的占比的时候，我们抓3个球，出现2黑1白的概率最大。我们直接用公式来说明。
假设黑球占比为P，白球为1-P。于是我们要求解MAX(PP(1-P))，显而易见P=67%（求解方法：对方程求导，使导数为0的P值即为最优解）
我们看逻辑回归，解决的是二分类问题，是不是和上面黑球白球问题很像，是的，逻辑回归也是最大似然概率来求解

假设我们有n个独立的训练样本{(x1, y1) ,(x2, y2),…, (xn, yn)}，y={0, 1}。那每一个观察到的样本(xi, yi)出现的概率是

由于y的取值是（0,1），当y=1的时候，后面那一项是不是没有了，那就只剩下x属于1类的概率，当y=0的时候，第一项是不是没有了，

那就只剩下后面那个x属于0的概率（1减去x属于1的概率）。所以不管y是0还是1，上面得到的数，都是(x, y)出现的概率。

那我们的整个样本集，也就是n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）：

这里我们稍微变换下L(θ)：取自然对数，然后化简：

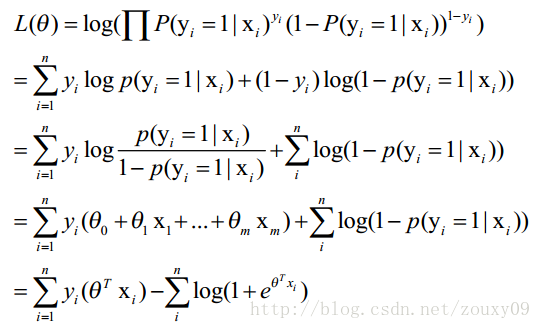
 第一步到第二步，结合下面这个看

 第二步到第三部，结合下面这个看

 

 

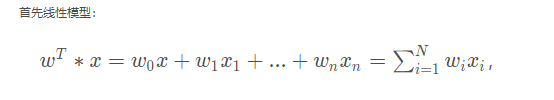
其中第三步到第四步使用了下面替换

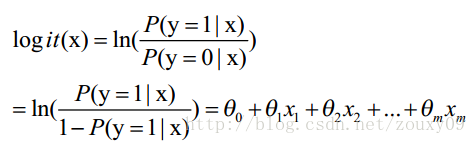
这时候为求最大值，对L(θ)对θ求导，得到：

然后我们令该导数为0，即可求出最优解。但是这个方程是无法解析求解（这里就不证明了）。
最后问题变成了，求解参数使方程L最大化，求解参数的方法梯度上升法（原理这里不解释了，看详细的代码的计算方式应该更容易理解些）。
根据替换公式，我们代入参数和特征，求P，也就是发生1的概率。

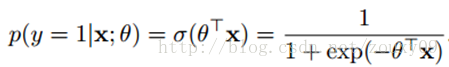
sigmoid函数，俗称激活函数，最后用于分类（若P(y=1|x;ΘThetaΘ )大于0.5，则判定为1）

=========================================================================================================================================

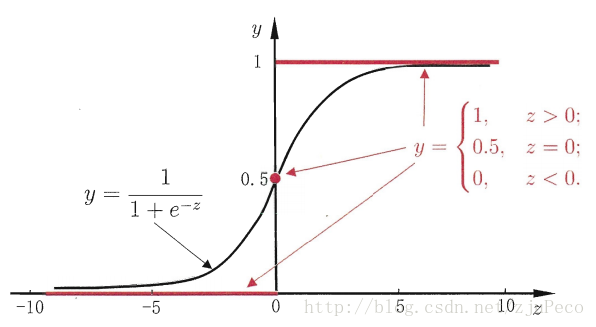
回答一下下面这些问题：

1. 什么是逻辑回归，逻辑回归的推导，损失函数的推导
2. 逻辑回归与SVM的异同
3. 逻辑回归与线性回归的不同
4. 为什么LR需要归一化或者取对数，为什么LR把特征离散化后效果更好
5. LR为什么用Sigmoid函数，这个函数有什么优缺点，为什么不用其他函数

 

1.逻辑回归概念（来自百度百科）：

logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。 

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。

 

逻辑回归的使用条件

1. 因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于Logistic回归。
2. 残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。二项分布可以认为是一种只有两种结果（成功/失败)的单次试验重复多次后成功次数的分布概率
3. 自变量和Logistic概率是线性关系
4. 各观测对象间相互独立。

原理：如果直接将线性回归的模型扣到Logistic回归中，会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量，某个概率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小。所以，才引入Logistic回归。 
Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。 
注意：如果自变量为字符型，就需要进行重新编码。一般如果自变量有三个水平就非常难对付，所以，如果自变量有更多水平就太复杂。这里只讨论自变量只有三个水平。非常麻烦，需要再设二个新变量。共有三个变量，第一个变量编码1为高水平，其他水平为0。第二个变量编码1为中间水平，0为其他水平。第三个变量，所有水平都为0。实在是麻烦，而且不容易理解。最好不要这样做，也就是，最好自变量都为连续变量。 

注意Logistic函数就是sigmoid函数

 logistic函数公式大概如下：

2.逻辑回归的推导

构造预测函数：

线性模型：

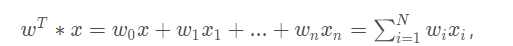
也可以写为：

  而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数

而逻辑函数（即是sigmoid函数）又等于：

即只需替换x

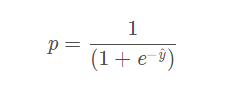
反过来再求y，则有：

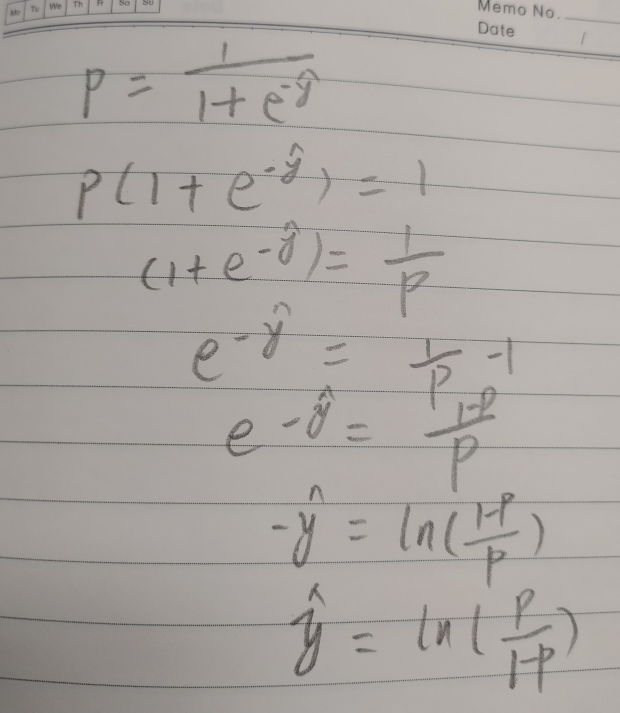
 即是：

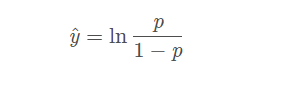
对于二分类问题函数 π(x) ，最大化样本概率就可以得到更优分类模型，所以有：

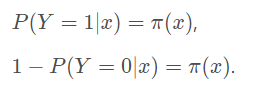
 整合为似然函数为：

 对数似然函数为（log减就是除）：

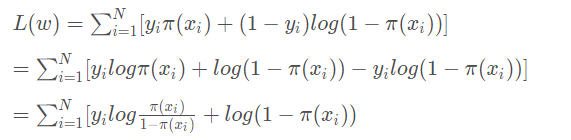
 上面说到

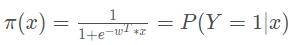
 令：

 得到：

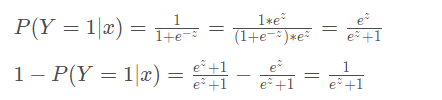
 所以求得其 logistlogistlogist函数为：

 代入对数似然函数：

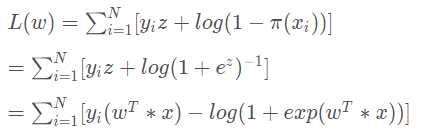
 下面又有一种推导方法

参考https://blog.csdn.net/weixin_39750084/article/details/83443945

逻辑回归的使用条件有说到，因变量服从二项分布，即样本的概率分布情况如下：

 

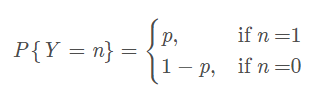
二项分布的最大似然估计法：

 进而不是用最小二乘法，而是最大似然法来解决方程估计和检验则似然函数如下：

 将概率值代入似然函数，得到

令代价函数为负的似然函数的对数，取对数为了求导方便，因为乘积求导很麻烦，那么使得似然函数（似然函数是后验概率的乘积，这篇文章：https://www.cnblogs.com/zhizhan/p/4113614.html 的例子很好，就是知道你已经头痛了，通过你的各种表现，即你的病理特征，来判断你是因为哪种原因感冒的，判断正确的样本越多，后验概率乘积越大。）最大的参数值就是使得代价函数最小的参数值。因此逻辑回归采用的是对数损失函数。具体的公式如下

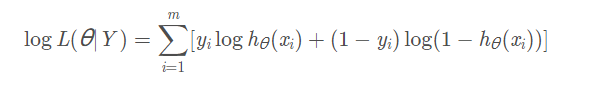
因为似然函数要最大化，而代价函数要最小化且需要求平均，因此转换成以下形式：

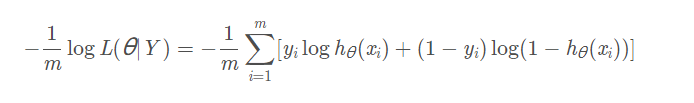
最终损失函数为：

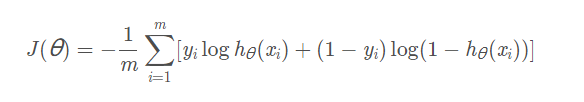
yi​是样本的真实值，hθ(x−i)是样本的预测值。知道代价函数之后，我们就能对参数进行求解了。依旧是根据以下公式更新：