导数

计算复合函数的导数时，关键是分析清楚复合函数的构造，即弄清楚该函数是由哪些基本初等函数经过这样的过程复合而成的，求导数时，按复合次序由最外层起，向内一层一层地对中间变量求导数，直到对自变量求导数为止

一、导数表：

序号	原函数	导函数
1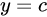
2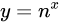
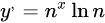3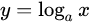
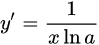4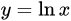
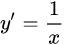5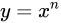
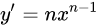6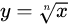
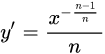7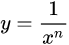
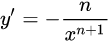8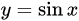
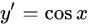9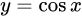
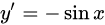10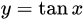
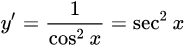11
12
13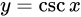
14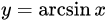
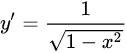15
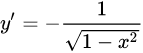16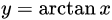
17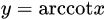
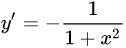18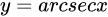
19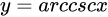
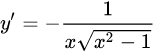20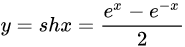
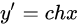21
22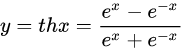
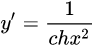23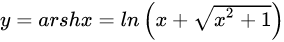
24
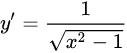25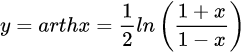

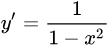二、推导依据：

在推导的过程中有这几个常见的公式需要用到：

1.链式法则：

 则：

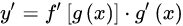
 f'[g(x)]中g(x) 看作整个变量，而g'(x) 中把x看作变量

 

2.y=u*v，则y'=u'v+uv'

 

3.如有

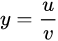
则：

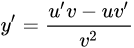
4.反函数求导法则：

y=f(x) 的反函数是x=g(y) ，则有

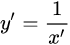
三、推导过程

指的是上面函数表的函数的导数推导过程

①显而易见，y=c是一条平行于x轴的直线，所以处处的切线都是平行于x的，故斜率为0。用导数的定义求证也是一样的：

②指数函数 与③对数函数

， 

推导过程：