一元线性回归模型

1.一元线性回归模型

 2.如何求里面的参数a,b

我们默认误差符合正态分布，那么利用最小二乘法，即可求参数a,b

 求最小值，也就是对a,b求偏导数

 

 

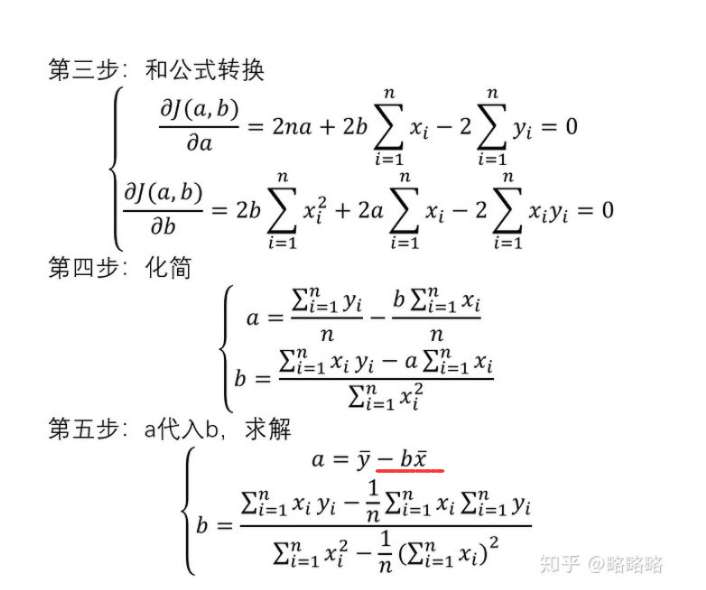
3.如何使用Python求这个值

第一种方法：

直接根据上面的公式去计算

import numpy as np
#生成数据
x = np.arange(0,20)
v = np.random.uniform(-10,+10,x.shape)#干扰，让数据有误差
y = 2 * x + v
plt.scatter(x,y)
# 简单线性回归模型的参数求解
# 样本量
n = x.shape
# 计算自变量、因变量、自变量平方、自变量与因变量乘积的和
sum_x = x.sum()
sum_y = y.sum()
sum_x2 = (x*x).sum()
xy = x * y
sum_xy = xy.sum()
# 根据公式计算回归模型的参数
b = (sum_xy-sum_x*sum_y/n)/(sum_x2-sum_x**2/n)
a = sum_y/n-b*sum_x/n
# 打印出计算结果
print('回归参数a的值：',a)  #[-0.31848548]
print('回归参数b的值：',b)  #[1.97134719]

y1=a+b*x
plt.scatter(x,y)
plt.plot(x,y1)

 

第二种方法：

statsmodel所示专门用于统计建模的第三方模块，如需实现线性回归模型的参数求解，可以调用子模块中的ols函数

该函数语法：

ols(formula,data,subset=None,drop_cols=None)

• fromula:以字符串形式指定线性回归的模型，y~x就表示简单线性回归模型
• data:指定建模的数据集
• subset:通过布尔类型的数组对象，获取data的子集用于建模
• drop_cols:指定需要从data中删除的变量

import statsmodels.api as sm
import pandas as pd 
data = pd.DataFrame()
data['x'] = x
data['y'] = y

#构建回归模型
fit = sm.formula.ols('y ~ x',data = data).fit()
fit.params

y2= 1.971347*x-0.318485
plt.scatter(x,y)
plt.plot(x,y1)
plt.plot(x,y2)

 

第三种方法：

使用sklearn库的算法

# 导入线性回归模块
from sklearn.linear_model import LinearRegression
model = LinearRegression() #创建线性回归模型
model.fit(x.reshape(-1,1),data.y) #进行拟合，将dataframe转换为ndarray形式,将xtrain转换为列维度
model.coef_  #查看斜率，即y=ax+b中的a
model.intercept_ #查看截距，即y=ax+b中的b
print('计算出来的值，a=%f,,,,b=%f'%(model.coef_,model.intercept_))  #计算出来的值，a=1.971347,,,,b=-0.318485
print('拟合函数为，y = %f * x  + %f'%(model.coef_,model.intercept_))  #拟合函数为，y = 1.971347 * x  + -0.318485

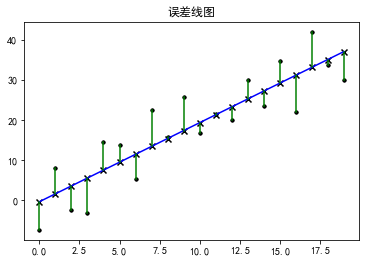
我们可以看出，其实这三种方法都可以计算出来，且值都非常接近（小数点问题而已），下面再画一下误差图

# 将相关结果进行绘图显示出来
fig = plt.figure()
ax = plt.subplot(111)
ax.scatter(x,y,marker='.',color='k',label='实际值')
plt.plot(x,y2,color='b',label='拟合线')
#这步是画误差值
plt.scatter(x,y,marker='.',color='k',label='原值')
plt.scatter(x,y2,marker='x',color='k',label='原值拟合值')
plt.plot([x,x],[y,y2],color='g')  #误差线
plt.title('误差线图')
plt.show() 

 文章参考这两位同学：

https://zhuanlan.zhihu.com/p/73494604?utm_source=qq

https://zhuanlan.zhihu.com/p/277698407