一、简介
LinkedList是一个常用的集合类,用于顺序存储元素。LinkedList经常和ArrayList一起被提及。大部分人应该都知道ArrayList内部采用数组保存元素,适合用于随机访问比较多的场景,而随机插入、删除等操作因为要移动元素而比较慢。LinkedList内部采用链表的形式存储元素,随机访问比较慢,但是插入、删除元素比较快,一般认为时间复杂都是O(1)(需要查找元素时就不是了,下面会说明)。本文分析LinkedList的具体实现。
二、数据结构
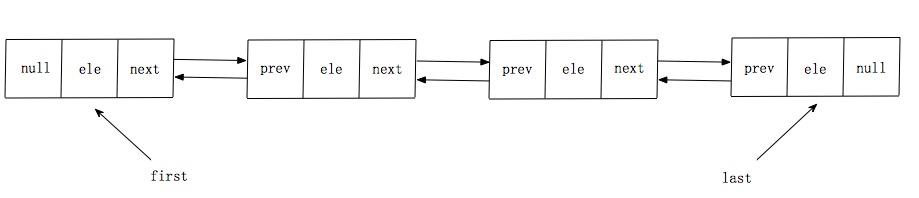
如上图所示,LinkedList底层使用的双向链表结构,有一个头结点和一个尾结点,双向链表意味着我们可以从头开始正向遍历,或者是从尾开始逆向遍历,并且可以针对头部和尾部进行相应的操作。
三、继承关系
public class LinkedList<E> extends AbstractSequentialList<E> implements List<E>, Deque<E>, Cloneable, java.io.Serializable
LinkedList 是一个继承于AbstractSequentialList的双向链表。它也可以被当作堆栈、队列或双端队列进行操作。该类调用ListIterator实现了元素的增删改查,在LinkedList被重写。
LinkedList 实现 List 接口,能对它进行队列操作。
LinkedList 实现 Deque 接口,即能将LinkedList当作双端队列使用。
LinkedList 实现了Cloneable 接口,即覆盖了函数clone(),能克隆。
LinkedList 实现Java.io.Serializable接口,这意味着LinkedList支持序列化,能通过序列化去传输。
LinkedList 是非同步的。
四、内部变量
transient int size = 0; transient Node<E> first; // 头节点 transient Node<E> last; // 尾节点
总共就三个内部变量,size是实际元素个数,first是指向第一个元素的指针,last则指向最后一个。注意,头结点、尾结点都有transient关键字修饰,这也意味着在序列化时该域是不会序列化的。
元素在内部被封装成Node对象,这是一个内部类,看一下它的代码:
private static class Node<E> { E item; // 数据域 Node<E> next; // 后继 Node<E> prev; // 前驱 // 构造函数,赋值前驱后继 Node(Node<E> prev, E element, Node<E> next) { this.item = element; this.next = next; this.prev = prev; } }
内部类Node就是实际的结点,用于存放实际元素的地方。我们可以看到这是一个双向链表的结构,每个节点保存它的前驱节点和后继节点。
五、构造函数
LinkedList一共有两个显示的构造函数,一个无参的,一个带参的:
public LinkedList() { }
默认构造方法是空的,什么都没做,表示初始化的时候size为0,first和last的节点都为空。
public LinkedList(Collection<? extends E> c) { // 调用无参构造函数 this(); // 添加集合中所有的元素 addAll(c); }
该构造函数会调用无参构造函数,并且会把集合中所有的元素添加到LinkedList中。
六、核心函数
1.私有方法
LinkedList内部有几个关键的私有方法,它们实现了链表的插入、删除等操作。比如在表头插入:
/* * 表头插入 */ private void linkFirst(E e) { final Node<E> f = first; // 先保存当前头节点 // 创建一个新节点,节点值为e,前驱节点为空,后继节点为当前头节点 final Node<E> newNode = new Node<>(null, e, f); first = newNode; // 让first指向新节点 if (f == null) // 如果链表原来为空,把last指向这个唯一的节点 last = newNode; else · // 否则原来的头节点的前驱指向新的头节点 f.prev = newNode; size++; // 元素数量+1 modCount++; // 结构修改性+1 }
其实就是双向链表的插入操作,调整指针的指向,时间复杂度为O(1),学过数据结构的应该很容易看懂。其它还有几个类似的方法:
// 尾部插入 void linkLast(E e) { // 保存尾结点,l为final类型,不可更改 final Node<E> l = last; // 新生成结点的前驱为l,后继为null final Node<E> newNode = new Node<>(l, e, null); // 重新赋值尾结点 last = newNode; if (l == null) // 如果链表原来为空,让first指向这个唯一的节点 first = newNode; else l.next = newNode; // 尾结点的后继为新生成的结点 size++; modCount++; } // 中间插入 void linkBefore(E e, Node<E> succ) { // assert succ != null; final Node<E> pred = succ.prev; final Node<E> newNode = new Node<>(pred, e, succ); succ.prev = newNode; if (pred == null) first = newNode; else pred.next = newNode; size++; modCount++; } // 删除头节点 private E unlinkFirst(Node<E> f) { // assert f == first && f != null; final E element = f.item; final Node<E> next = f.next; // 先保存下一个节点 f.item = null; f.next = null; // help GC first = next; // 让first指向下一个节点 if (next == null) // 如果下一个节点为空,说明链表原来只有一个节点,现在成空链表了,要把last指向null last = null; else // 否则下一个节点的前驱节点要置为null next.prev = null; size--; // 元素个数-1 modCount++; // 结构修改性+1 return element; } // 删除尾节点 private E unlinkLast(Node<E> l) { // assert l == last && l != null; final E element = l.item; final Node<E> prev = l.prev; // 保存前一个节点 l.item = null; l.prev = null; // help GC last = prev; // last指向前一个节点 if (prev == null) // 与头节点删除一样,判断是否为空 first = null; else prev.next = null; size--; modCount++; return element; } // 从链表中间删除节点 E unlink(Node<E> x) { // 保存结点的元素 final E element = x.item; // 保存x的后继 final Node<E> next = x.next; // 保存x的前驱 final Node<E> prev = x.prev; if (prev == null) { // 前驱为空,表示删除的结点为头结点 first = next; // 重新赋值头结点 } else { // 删除的结点不为头结点 prev.next = next; // 赋值前驱结点的后继 x.prev = null; // 结点的前驱为空,切断结点的前驱指针 } if (next == null) { // 后继为空,表示删除的结点为尾结点 last = prev; // 重新赋值尾结点 } else { // 删除的结点不为尾结点 next.prev = prev; // 赋值后继结点的前驱 x.next = null; // 结点的后继为空,切断结点的后继指针 } x.item = null; // 结点元素赋值为空 // 减少元素实际个数 size--; // 结构性修改加1 modCount++; // 返回结点的旧元素 return element; }
2.公有方法
2.1 add函数
public boolean add(E e) { // 添加到末尾 linkLast(e); return true; }
add函数用于向LinkedList中添加一个元素,并且添加到链表尾部。具体添加到尾部的逻辑是由linkLast函数完成的。
对于添加元素的情况我们使用如下示例进行说明
示例一代码如下(只展示核心代码)
List<Integer> lists = new LinkedList<>(); lists.add(5); lists.add(6);

上图的表明了在执行每一条语句后,链表对应的状态。
2.2 add(int index, E element)函数
public void add(int index, E element) { checkPositionIndex(index); // 检查索引合法性 if (index == size) // 判断是否在链尾 linkLast(element); // 是就直接插入到链表末尾 else linkBefore(element, node(index)); }
在列表中特定的位置插入指定的元素
2.3 addAll函数
addAll有两个重载函数,addAll(Collection<? extends E>)型和addAll(int, Collection<? extends E>)型,我们平时习惯调用的addAll(Collection<? extends E>)型会转化为addAll(int, Collection<? extends E>)型,所以我们着重分析此函数即可。
public boolean addAll(int index, Collection<? extends E> c) { // 检查插入的的位置是否合法 checkPositionIndex(index); // 将集合转为数组(优化) Object[] a = c.toArray(); // 保存集合大小 int numNew = a.length; // 集合为空直接返回 if (numNew == 0) return false; // 前驱,后继 Node<E> pred, succ; if (index == size) { // 如果插入位置为链表末尾,则后继为null,前驱为尾结点 succ = null; pred = last; } else { // 插入位置为其他某个位置 succ = node(index); // 找到该节点 pred = succ.prev; // 保存该节点的前驱 } // 循环遍历a数组,然后将a数组里面的元素创建成拥有前后连接的节点,之后一个个按照顺序连起来 for (Object o : a) { @SuppressWarnings("unchecked") E e = (E) o; // 向下转型 // 生成新节点 Node<E> newNode = new Node<>(pred, e, null); if (pred == null) { // 表示在第一个元素之前插入(索引为0的结点) first = newNode; } else { pred.next = newNode; } pred = newNode; } if (succ == null) { // 表示在最后一个元素之后插入 last = pred; } else { pred.next = succ; succ.prev = pred; } // 修改实际元素个数 size += numNew; modCount++; // 结构性修改加1 return true; }
参数中的index表示在索引下标为index的结点(实际上是第index + 1个结点)的前面插入。在addAll函数中,addAll函数中还会调用到node函数,get函数也会调用到node函数,此函数是根据索引下标找到该结点并返回,具体代码如下
Node<E> node(int index) { // 判断插入的位置在链表前半段或者是后半段 if (index < (size >> 1)) { // 插入位置在前半段 Node<E> x = first; for (int i = 0; i < index; i++) // 从头结点开始正向遍历 x = x.next; return x; // 返回该结点 } else { // 插入位置在后半段 Node<E> x = last; for (int i = size - 1; i > index; i--) // 从尾结点开始反向遍历 x = x.prev; return x; // 返回该结点 } }
在根据索引查找结点时,会有一个小优化,结点在前半段则从头开始遍历,在后半段则从尾开始遍历,这样就保证了只需要遍历最多一半结点就可以找到指定索引的结点。
此时插入操作的时间复杂度就不是O(1),而是O(n/2)+O(1)
下面通过示例来更深入了解调用addAll函数后的链表状态。
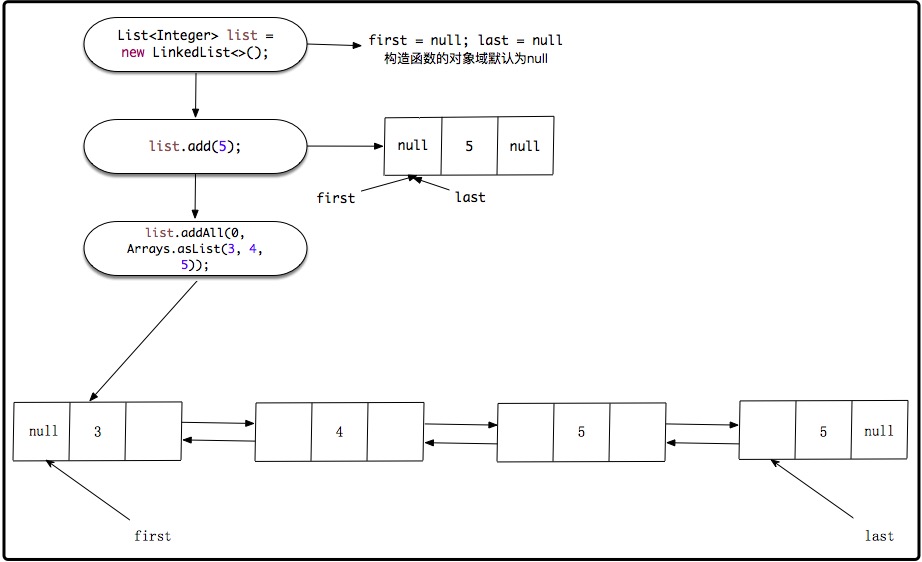
List<Integer> list = new LinkedList<>(); list.add(5); list.addAll(0, Arrays.asList(3, 4, 5));
上述代码内部的链表结构如下:
3. remove方法
/** * 删除指定位置的元素 */ public E remove(int index) { checkElementIndex(index); // 检查是否越界 return unlink(node(index)); // 用node方法找到该位置的元素并用unlink方法删除掉该节点 } /** * 删除列表中出先的第一个指定元素 */ public boolean remove(Object o) { if (o == null) { // 传入的元素为null for (Node<E> x = first; x != null; x = x.next) { if (x.item == null) { // 找到第一个循环遍历到的null元素 unlink(x); // 并删除 return true; } } } else { for (Node<E> x = first; x != null; x = x.next) { if (o.equals(x.item)) { unlink(x); return true; } } } return false; }
第一个remove(int index)方法同样要调用node(index)寻找节点。而第二个方法remove(Object o)是删除指定元素,这个方法要依次遍历节点进行元素的比较,最坏情况下要比较到最后一个元素,比调用node方法更慢,时间复杂度为O(n)。另外从这个方法可以看出LinkedList的元素可以是null。
4.set方法
public E set(int index, E element) { checkElementIndex(index); // 检查是否越界 Node<E> x = node(index); // 取得该索引上的元素 E oldVal = x.item; // 保存旧元素 x.item = element; // 将指定的元素赋给该索引上的元素 return oldVal; // 返回旧元素 }
检查设置元素位然后置是否越界,如果没有,则索引到index位置的节点,将index位置的节点内容替换成新的内容element,同时返回旧值。
5.get方法
public E get(int index) { checkElementIndex(index); return node(index).item; }
首先是判断索引位置有没有越界,确定完成之后开始遍历链表的元素,调用之前的node方法获取到对应的元素。
至此基础的增删改查操作都分析完毕,其他的方法的实现也均建立在这些基础方法之上的,在此就不一一列举分析了,更多的是对容器的增删改查操作。
总结
-
LinkedList基于双向链表实现,元素可以为null。 -
LinkedList插入、删除元素比较快,如果只要调整指针的指向那么时间复杂度是O(1),但是如果针对特定位置需要遍历时,时间复杂度是O(n)。 - 函数addAll中的优化操作,感觉有点类似于二分查找,传入一个集合参数和插入位置,然后将集合转化为数组,然后再遍历数组,挨个添加数组的元素,但是问题来了,为什么要先转化为数组再进行遍历,而不是直接遍历集合呢?从效果上两者是完全等价的,都可以达到遍历的效果。关于为什么要转化为数组的问题,思考如下:1. 如果直接遍历集合的话,那么在遍历过程中需要插入元素,在堆上分配内存空间,修改指针域,这个过程中就会一直占用着这个集合,考虑正确同步的话,其他线程只能一直等待。2. 如果转化为数组,只需要遍历集合,而遍历集合过程中不需要额外的操作,所以占用的时间相对是较短的,这样就利于其他线程尽快的使用这个集合。说白了,就是有利于提高多线程访问该集合的效率,尽可能短时间的阻塞。