数据结构和算法绪论

程序设计 = 数据结构 + 算法

数据结构：逻辑结构（数据对象中数据元素之间的相互关系）和物理结构（数据的逻辑结构在计算机中的存储形式）。

　　逻辑结构：集合结构（只有同属一个集合的关系）、线性结构（一对一的关系）树形结构（存在一对多的层次关系）、图形结构（多对多的关系）。

　　物理结构：顺序存储（把数据放在地址连续的存储单元里，数据间的逻辑关系和物理关系一致）、链式存储（任意存储单元，数据元素的存储关系不能反映其逻辑关系，需要用一个指针存放数据元素的地址）。

常用抽象数据类型：

算法的五个特性：输入（零个或多个输入）、输出（至少一个输出）、有穷性（有限步骤后结束，每个步骤在可接受时间内完成）、确定性（每个步骤都被精确定义无歧义；在一定条件下只有一条执行路径）、可行性（每个步骤都能通过执行有限次数完成）。

算法设计的要求：

　　1. 正确性：没有语法错误；对合法输入产生满足要求的输出；对非法输入产生满足规格的说明；对故意刁难的测试输入都有满足要求的输出结果。

　　2. 可读性：便于阅读。

　　3. 鲁棒性：输入数据不合法也能做出相关处理。

　　4. 时间效率高和存储量低。

时间复杂度和空间复杂度

事先分析估算。时间消耗取决于：算法采用的策略、编译产生的代码质量、问题的输入规模、机器执行指令的速度。（所以抛开硬软件因素，程序运行所需时间依赖于算法好坏和输入规模）

分析算法的运行时间时，要把程序看成是独立于程序设计语言的算法或一系列步骤，把基本操作的数量和输入模式关联起来。

判断算法效率时，函数中的常数和其他其他次要项可以忽略，主要关注最高项的阶数。T(n) = O(f(n))，随问题规模 n 的增大，算法执行时间的增长率和f(n)的增长率相同，称为渐进时间复杂度（即时间复杂度），一般关注最坏时间复杂度。

大O阶方法：

　　1. 常数 1 取代运行时间中的所有加法常数。

　　2. 只保留最高阶项，且不保留最高阶项的系数。

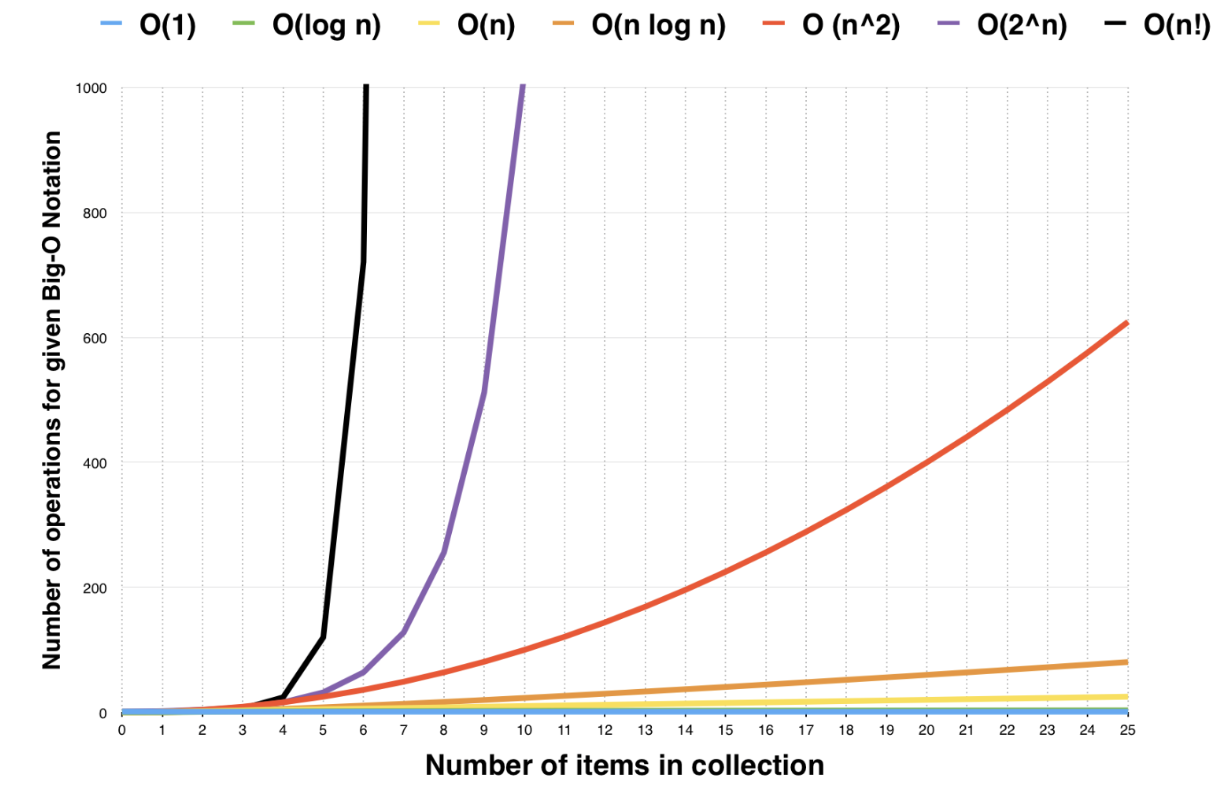
常用时间复杂度：O(1) < O(logn)< O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

斐波那契数列

def fib(n):
    if n == 0 or n == 1:
        return n
    return fib(n-1) + fib(n-2)

递归方法的时间复杂度为O(2ⁿ)

一些递归方法的时间复杂度：

  

空间复杂度指算法所需的存储空间，S(n) = O(f(n))