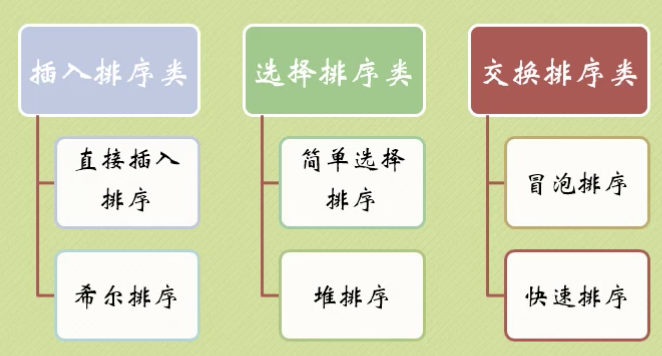
排序算法的稳定性：一个稳定的排序算法，如果两个等值键R和S在排序前后次序不变，称其是稳定的
例如排序之前的序列为：(4, 1) (3, 1) (3, 7)（5, 6）
(3, 1) (3, 7) (4, 1) (5, 6) 维持次序，稳定
(3, 7) (3, 1) (4, 1) (5, 6) 次序被改变，不稳定
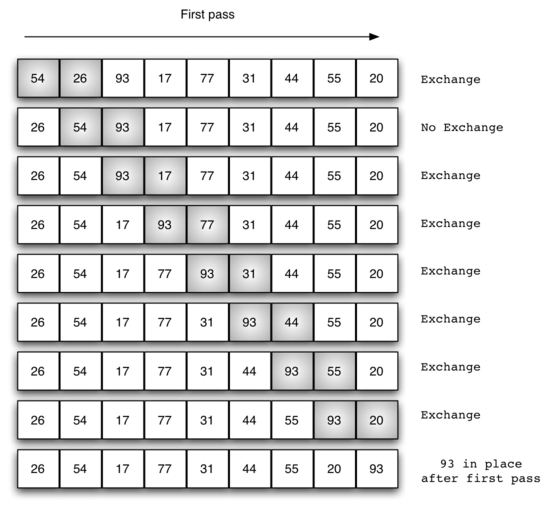
1.冒泡排序
两两相邻记录的关键字，如果反序就交换，直到没有反序的记录为止。
# 直觉的写法，但实际不能算冒泡
def bubble_sort(alist):
for i in range(len(alist)-1): # 从第一个元素到倒数第二个元素
for j in range(i+1, len(alist)): # 如果a[i]比后面的元素更大，交换
if alist[i] > alist[j]:
alist[i], alist[j] = alist[j], aslit[i]
因为实际上每次固定的a[i]会和后面的所有元素都比较一遍，并不是冒泡中的比较两两相邻的关键字。
两两是相邻元素；如果有n个元素那就要比较n-1轮，每一轮都减少一次比较；从下往上两两比较，就像泡泡往上冒一样。
# 升序
def bubble_sort(alist):
n = len(alist)
for i in range(n-1): # 当前轮从a[i]开始，两两相邻比较，最后一轮从a[n-2]开始。a[:i]已经有序
for j in range(n-1, i, -1): # 从下向上冒
if alist[j] < alist[j-1]: # 如果后一个元素比前一个小，就交换
alist[j], alist[j-1] = alist[j-1], alist[j]
做一点优化
def bubble_sort_pro(alist):
n = len(alist)
for i in range(n-1):
count = 0
for j in range(n-1, i, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
count += 1
if count == 0: # 如果某一轮没有进行任何交换，说明整个数组已经有序了
return
2.选择排序
通过n-i次关键字之间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i个记录交换。1<=i<=n。
在未排序序列中找到最小（大）元素，放到已排序序列起始位置（一次交换）；
然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾（一次交换）；
以此类推，直到所有元素均排序完毕
选择排序的优点在于数据移动的操作：如果某个元素位于正确的最终位置上，它就不会被移动。所以至多需要交换 n-1 次（因为第一次就直接认为第一个元素是最小（大））。操作的是无序的那部分。
def selection_sort(alist):
n = len(alist)
for i in range(n-1): # 要找 n-1 轮最值，第一个首先认为是个最小（大）值
min_index = i # 记录当前的最小（大）位置
for j in range(i+1, n): # 遍历剩下无序部分的元素，找出最小的，再交换
if alist[j] < alist[min_index]:
min_index = j
if min_index != i:
alist[i], alist[min_index] = alist[min_index], alist[i]
3.直接插入排序
简单排序中性能最好的。将一个记录插入到一个已经排好序的有序表中。
通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。所以过程中需反复把已经排序的元素向后挪。
操作的是有序的那部分。
def insert_sort(alist):
n = len(alist)
for i in range(1, n):
for j in range(i, 0, -1): # 待插入元素为a[i]，有序序列为a[:i]
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j] # a[i]从后往前比较，找到插入位置。就相当于一直交换。
优化
def insert_sort_pro(alist):
n = len(alist)
for i in range(1, n):
j = i
while j > 0:
# 寻找插入位置，只要没到位置，一直交换，最终插入
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
j -= 1
else: # 如果找到要插入的位置了就不用往前再看了，避免了多余的循环
break
4.希尔排序
时间复杂度降到O(nlogn)，对直接插入排序进行修改。
把记录按下标的一定增量（gap）分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个记录恰被分成一组，算法终止。
例如下图就是第一轮分了5组，第二轮分了2组
# 按gap进行插入排序
def shell_sort(alist):
n = len(alist)
gap = n // 2
while gap > 0:
for i in range(gap, n): # 从 0+gap 开始往后找元素往有序序列中插入，一直找到最后
j = i
while j >= gap and alist[j] < alist[j-gap]: # 每个子序列的j元素的前一个元素不再是j-1而是j-gap，因为要在a[j]属于的分组里做插入排序
alist[j-gap], alist[j] = alist[j], alist[j-gap]
j -= gap
gap //= 2 # 新步长
def shell_sort(alist):
n = len(alist)
gap = n // 2
while gap > 0:
for i in range(gap, n): # 待插元素从a[gap]到最后
for j in range(i, 0, -gap): # a[i]找插入位置，每次不再向前挪1而挪gap即可
if alist[j] < alist[j-gap]:
alist[j], alist[j-gap] = alist[j-gap], alist[j]
gap //= 2
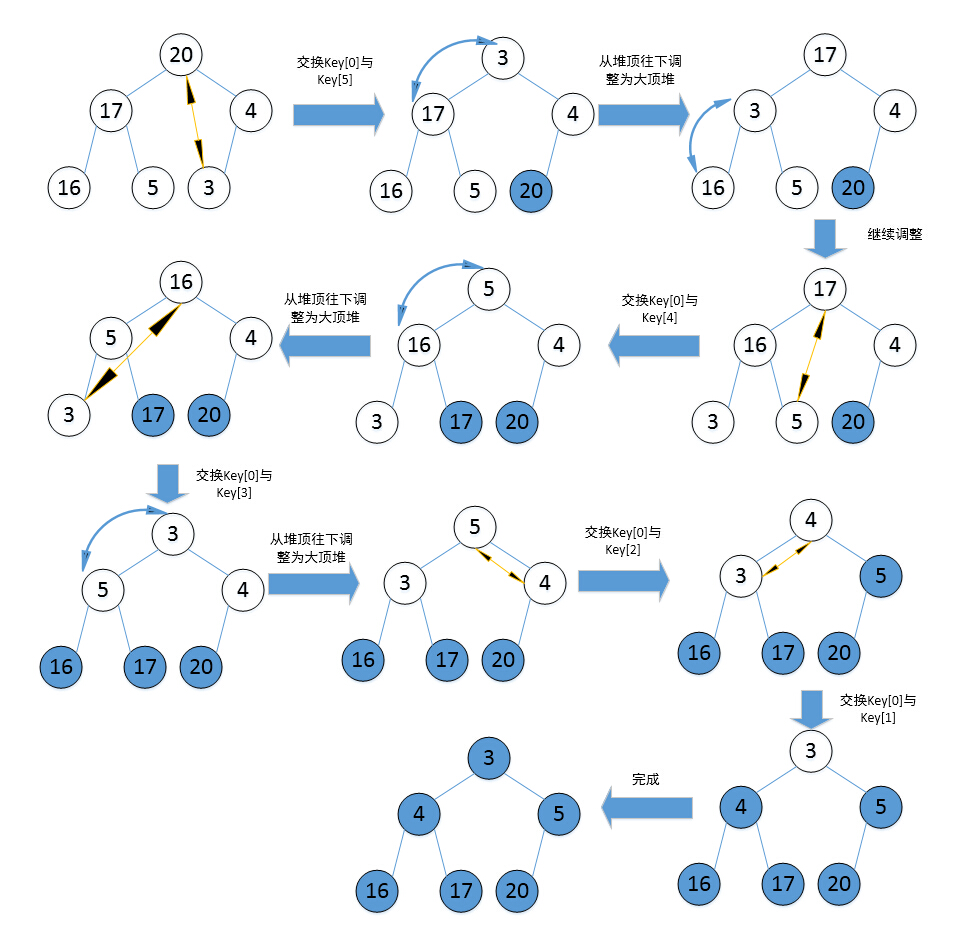
5.堆排序
利用前一趟比较的结果，对选择排序进行改进。堆是具有以下性质的完全二叉树：每个节点的值都大于等于（小于等于）其左右孩子节点的值。
大顶堆 & 小顶堆
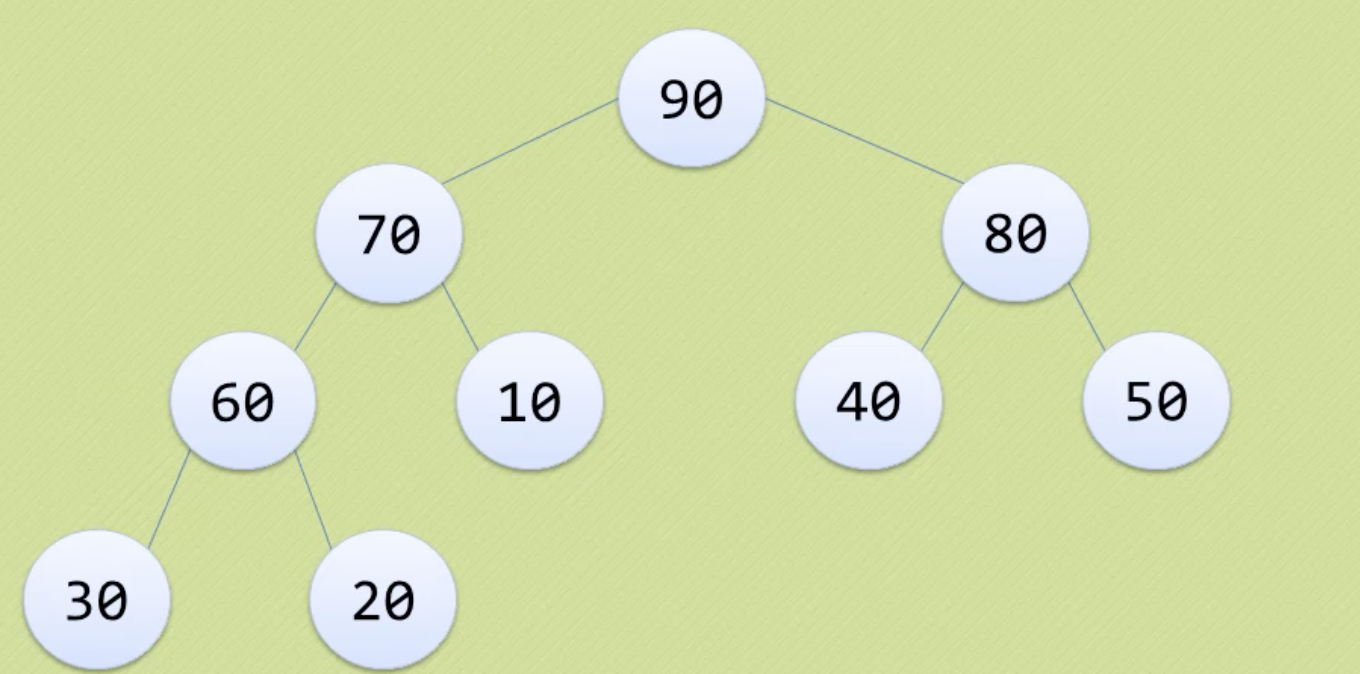
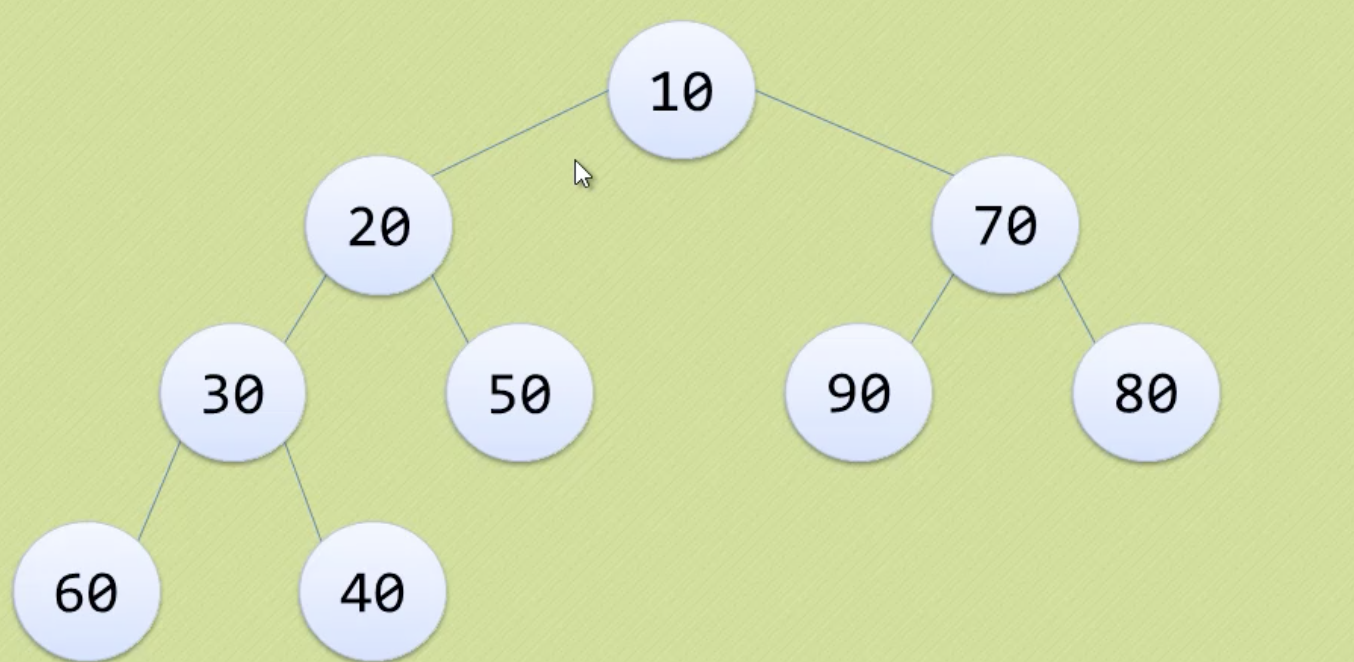
1. 将待排序的序列构造成一个大顶堆（或小顶堆）
2. 整个序列的最大值就是堆顶的根节点，将它移走（与堆数组的末尾元素交换，此时末尾元素就是最大值）。
3. 将剩余的n-1个序列重新构造成一个堆，重复上述步骤，获得升序序列。
升序排序，使用大顶堆。
堆具有的性质，如果从堆的根节点开始从1往后编号，则节点的值满足：
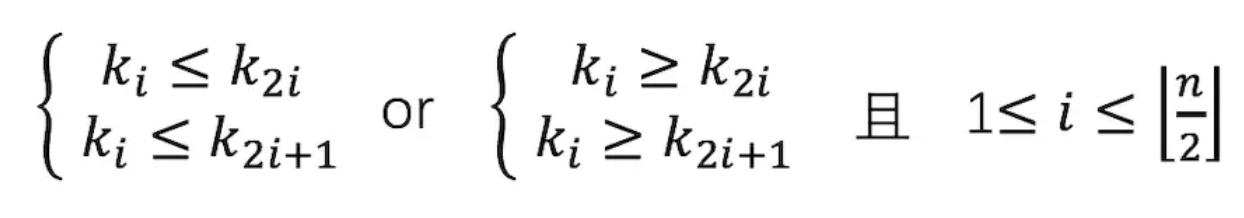，n/2向下取整。
树节点编号从1开始而数组下标从0开始。统一成从0开始计数，父节点 i 的左右孩子节点在2i+1、2i+2，子节点 i 的父节点在 floor((i-1)/2)
def heapify(arr, lst, i):
"""维护最大堆，以i为根节点的子树，最后一个节点lst"""
largest = i
left, right = 2*i+1, 2*i+2
# 找到 i、i的左子树、i的右子树中的最大值
if left <= lst and arr[i] < arr[left]:
largest = left
if right <= lst and arr[largest] < arr[right]:
largest = right
# 如果这三个节点中最大的不是i，则最大节点的值和i的值交换
if largest != i:
arr[largest], arr[i] = arr[i], arr[largest]
heapify(arr, lst, largest) # 继续对largest节点递归维护堆。如果i是最大的元素，则函数结束
def heap_sort(arr):
n = len(arr)
for i in range(int((n-1-1)/2), -1, -1): # 从最后一个节点n-1的父节点开始往顶上，第一个要维护的子树根节点为 floor(((n-1)-1)/2)
heapify(arr, n-1, i)
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 堆顶a[0] 和 当前堆的最后一个元素（如果认为每次都把排好的移除。实际就是arr[i]）交换
heapify(arr, i-1, 0) # 交换后要从顶向下维护堆，堆最后一个节点为下标为i-1
a = [3,4,1,2,9,5,6,8]
heap_sort(a)
print(a)
优化，把heapify函数中的尾部递归用迭代实现，效率更高
def heapify(arr, lst, i):
"""维护最大堆，以i为根节点的子树，最后一个节点lst"""
while True:
largest = i
left, right = 2*i+1, 2*i+2
# 找到 i、i的左子树、i的右子树中的最大值
if left <= lst and arr[i] < arr[left]:
largest = left
if right <= lst and arr[largest] < arr[right]:
largest = right
# 如果这三个节点中最大还是i，则函数结束
if largest == i:
break
arr[largest], arr[i] = arr[i], arr[largest] # 否则的把最大值换到当前根节点i上
i = largest # 继续下一轮，对当前的largest为根节点的子树进行维护
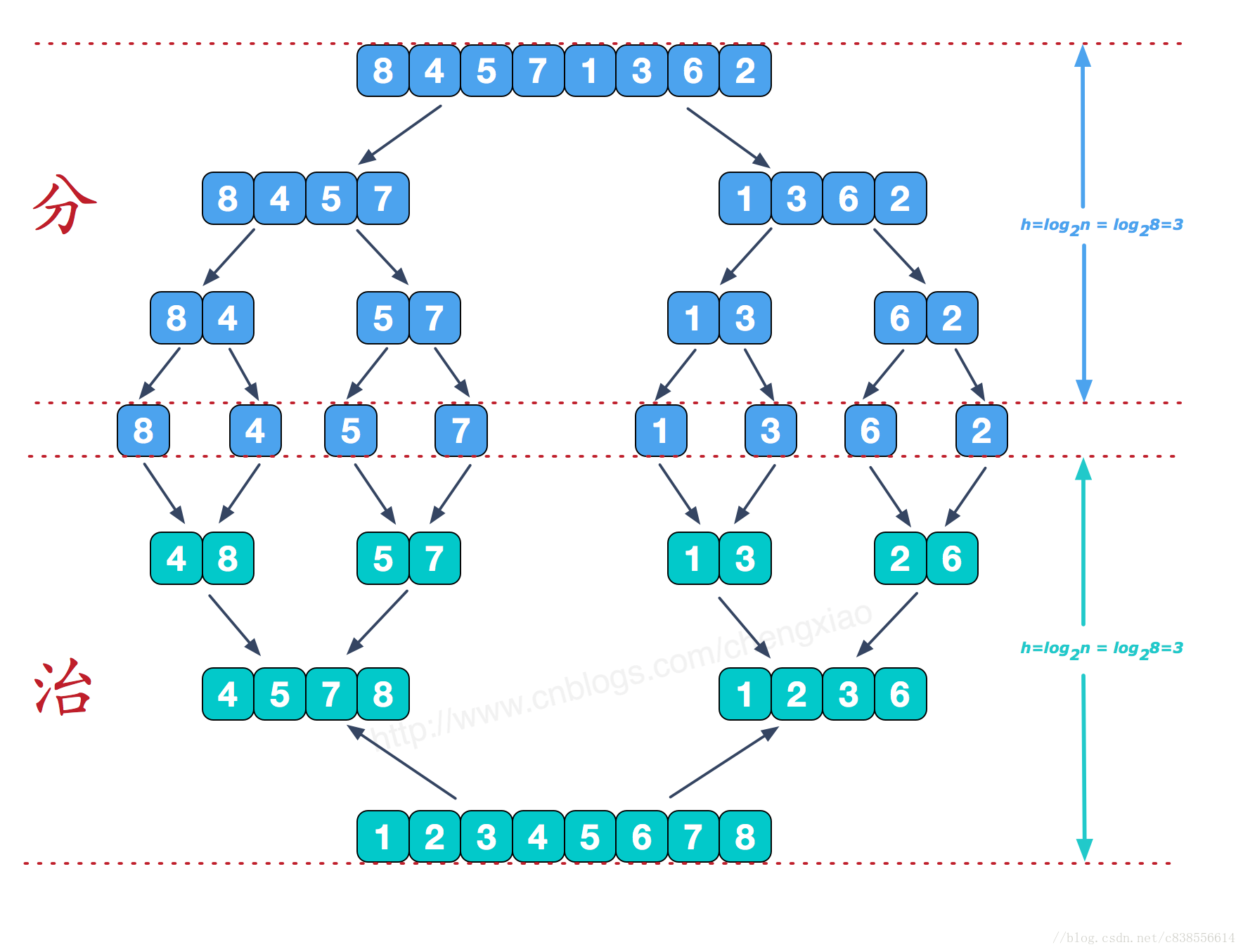
6.归并排序
分治思想，先递归分解数组，再合并数组。
将数组分解最小之后，把n个记录看成是n个有序的子序列，每个子序列长度为1。然后两两归并，得到ceil(n/2)个长度为2或者1的有序子序列，再两两归并...，如此重复直到得到长度为n的有序序列为止。
其中两两归并的基本思路是，比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。
def merge_sort(alist):
if len(alist) <= 1:
return alist
# 二分分解
num = len(alist)//2
left = merge_sort(alist[:num])
right = merge_sort(alist[num:])
# 合并
return merge(left,right)
def merge(left, right):
'''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
#left与right的下标指针
l, r = 0, 0
result = []
while l<len(left) and r<len(right):
if left[l] < right[r]:
result.append(left[l])
l += 1
else:
result.append(right[r])
r += 1
if l < len(left):
result += left[l:]
elif r < len(right):
result += right[r:]
return result
迭代实现，直接从下往上。
def merge_sort(alist):
if alist is None or len(alist) <= 1:
return alist
# 每次要合并的两组数组为 a[low, low+i]、a[low+i, low+2*i]
n = len(alist)
tmp = [0]*n # 建立临时数组
i = 1 # 步长，也就是合并后数组元素的一半。第一次合并后数组长度为2，所以i初始化为1
while i < n: # 最后一次合并之前i不超过n。例如考虑n=5的情况，i=1,2,4，最后i=4合并长度为4，1的两组后结束，下一轮i=8，超过n了
# 开始一趟，两两合并所有分组数组，每一趟都从头开始
low = 0
while low < n:
mid = low + i
high = min(low + 2*i, n) # 如果第二组越界了，high等于n即可。数组a[n]会越界，但a[:n]不会，等价于a[:]
if mid < high: # 只有存在第二组才需要merge。而第二组只要有元素，high一定大于等于mid+1
# merge
merge(alist, low, mid, high, tmp)
low += 2*i # 下两组的起始元素在上两组最后元素之后
i *= 2 # 每一趟合并全部结束后，下一趟步长翻倍
def merge(alist, low, mid, high, tmp):
"""这里merge要考虑分组数组长度为1的情况，还有high等于n的情况
所以还是用索引在长度上移动来遍历，比较不容易出错
"""
l, r, k = 0, 0, 0
len_l, len_r = len(alist[low: mid]), len(alist[mid: high]) # 两个数组的长度
while l < len_l and r < len_r: # 只要有一个数组遍历完了，补上没有遍历完的即可
if alist[low + l] < alist[mid + r]:
tmp[k] = alist[low + l]
k += 1
l += 1
else:
tmp[k] = alist[mid + r]
k += 1
r += 1
if l < len_l:
tmp[k: k + mid - (low + l)] = alist[low + l: mid]
alist[low: high] = tmp[: k + mid - (low + l)]
if r < len_r:
tmp[k: k + high - (mid + r)] = alist[mid + r: high]
alist[low: high] = tmp[: k + high - (mid + r)]
alist = [54,26,93,17,77,31,44,55,20]
merge_sort(alist)
print(alist)
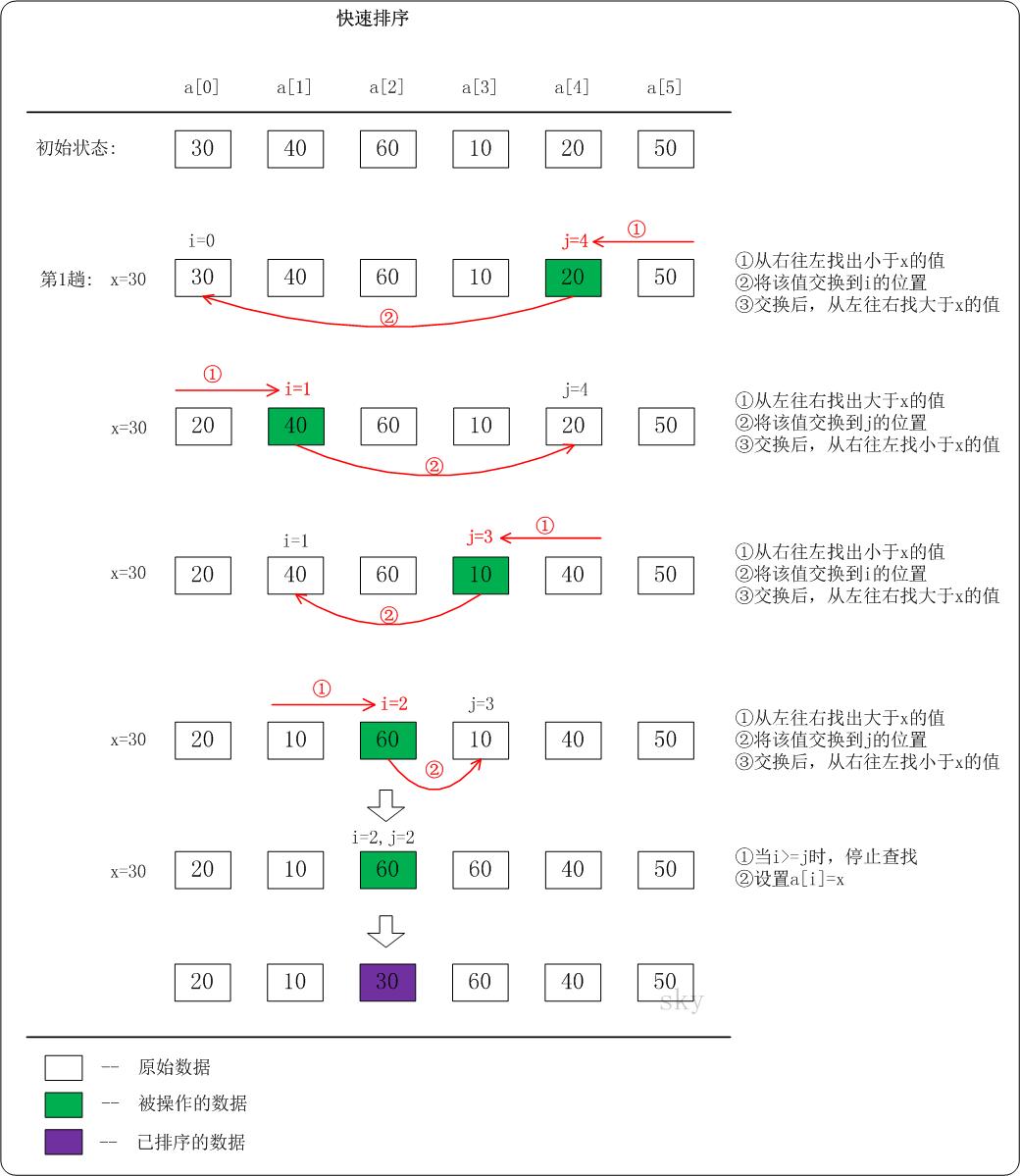
7.快速排序
通过一趟排序将要排序的数据分割成独立的两部分（选择一个比较基准），其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行。
步骤：
挑一个元素作为基准，重排元素，比基准大的放基准后面，比基准小的放基准前面；
递归的把两个子序列进行用上述方法分别排序
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if low < high:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
Qsort(arr, low, point-1)
Qsort(arr, point+1, high)
def Partition(arr, low, high):
# 起始元素为要寻找位置的基准元素，先把基准点的值拿出来，序列中始终就有一个多余的空位
point_value = arr[low] # 基准点初始化为起始元素
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low], arr[high] = arr[high], arr[low] # 交换，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high], arr[low] = arr[low], arr[high] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置
return low
快速排序的优化
1. 优化基准点的选取，三数取中法，基准点选取三个数中间大小的那个，避免极端情况，提高性能。
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if low < high:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
Qsort(arr, low, point-1)
Qsort(arr, point+1, high)
def Partition(arr, low, high):
# 令基准点介于a[low]和a[high]之间
mid = low + (high - low) // 2
if arr[mid] > arr[high]:
arr[mid], arr[high] = arr[high], arr[mid]
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
if arr[mid] > arr[low]:
arr[low], arr[mid] = arr[mid], arr[low]
point_value = arr[low] # 基准点
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low], arr[high] = arr[high], arr[low] # 交换，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high], arr[low] = arr[low], arr[high] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置
return low
2. 优化不必要的交换，直接改成赋值就行了，因为先把基准元素拿出来了，始终有一个位置是空余的。
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if low < high:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
Qsort(arr, low, point-1)
Qsort(arr, point+1, high)
def Partition(arr, low, high):
# 令基准点介于a[low]和a[high]之间
mid = low + (high - low) // 2
if arr[mid] > arr[high]:
arr[mid], arr[high] = arr[high], arr[mid]
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
if arr[mid] > arr[low]:
arr[low], arr[mid] = arr[mid], arr[low]
point_value = arr[low] # 基准点
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low]= arr[high] # 赋值，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high] = arr[low] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置，填回去
return low
3. 优化小数组时的排序方案，数组长度小于7的时候用直接插入排序。
def InsertSort(alist, low, high): # 修改一下插入排序，只排序alist中low到high这一段
for i in range(low+1, high+1):
for j in range(i, low, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high, MAX_LENGTH_INSERT_SORT=7):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if high - low > MAX_LENGTH_INSERT_SORT:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
Qsort(arr, low, point-1)
Qsort(arr, point+1, high)
else: # 数组小的话就直接插入
InsertSort(arr, low, high)
def Partition(arr, low, high):
# 令基准点介于a[low]和a[high]之间
mid = low + (high - low) // 2
if arr[mid] > arr[high]:
arr[mid], arr[high] = arr[high], arr[mid]
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
if arr[mid] > arr[low]:
arr[low], arr[mid] = arr[mid], arr[low]
point_value = arr[low] # 基准点
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low]= arr[high] # 赋值，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high] = arr[low] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置，填回去
return low
4. 优化递归操作，只要有可能，就把递归写成尾递归（函数中的递归形式出现在末尾），能够提高运行效率。尾递归可以比较容易的写成迭代。
def InsertSort(alist, low, high): # 修改一下插入排序，只排序alist中low到high这一段
for i in range(low+1, high+1):
for j in range(i, low, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high, MAX_LENGTH_INSERT_SORT=7):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if high - low > MAX_LENGTH_INSERT_SORT:
while low < high:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
Qsort(arr, low, point-1)
# 现在 low 已经没用了，后半部分的递归是point+1到high，如果令low=point+1，则可以在用循环在下一轮实现point+1到high的递归
low = point + 1 # 把尾递归写成while循环
else: # 数组小的话就直接插入
InsertSort(arr, low, high)
def Partition(arr, low, high):
# 令基准点介于a[low]和a[high]之间
mid = low + (high - low) // 2
if arr[mid] > arr[high]:
arr[mid], arr[high] = arr[high], arr[mid]
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
if arr[mid] > arr[low]:
arr[low], arr[mid] = arr[mid], arr[low]
point_value = arr[low] # 基准点
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low]= arr[high] # 赋值，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high] = arr[low] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置，填回去
return low
进一步地，要充分发挥递归的优势，加一个判断，令长度大的那部分用循环代替尾递归
def InsertSort(alist, low, high): # 修改一下插入排序，只排序alist中low到high这一段
for i in range(low+1, high+1):
for j in range(i, low, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
def quick_sort(alist):
Qsort(alist, 0, len(alist)-1)
def Qsort(arr, low, high, MAX_LENGTH_INSERT_SORT=7):
"""待排序数组arr, 起始位置low, 末尾位置high
"""
if high - low > MAX_LENGTH_INSERT_SORT:
while low < high:
point = Partition(arr, low, high) # 根据基准点a[point]处理数组，小的放基准点左边大的放基准点右边
if point - low < high - point: # 后半数组长度大
Qsort(arr, low, point - 1)
# 现在 low 已经没用了，后半部分的递归是point+1到high，如果令low=point+1，则可以在用循环在下一轮实现point+1到high的递归
low = point + 1 # 把尾递归写成while循环
else:
Qsort(arr, point + 1, high) # 现在high已经没用了
high = point - 1
else: # 数组小的话就直接插入
InsertSort(arr, low, high)
def Partition(arr, low, high):
# 令基准点介于a[low]和a[high]之间
mid = low + (high - low) // 2
if arr[mid] > arr[high]:
arr[mid], arr[high] = arr[high], arr[mid]
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
if arr[mid] > arr[low]:
arr[low], arr[mid] = arr[mid], arr[low]
point_value = arr[low] # 基准点
# 两个游标，low自左向右，high自右向左
while low < high:
while low < high and arr[high] >= point_value: # high游标自右向左找到比基准元素小的元素位置
high -= 1
arr[low]= arr[high] # 赋值，把比基准点小的放前面
while low < high and arr[low] < point_value: # low游标自左向右找到比基准元素大的元素位置
low += 1
arr[high] = arr[low] # 交换，把比基准点大的放后面
alist[low] = point_value # 当low与high位置重合，这就是基准点在最终序列中的位置，填回去
return low