1.圆圈中最后剩下的数

1 class Solution: 2 def LastRemaining_Solution(self, n, m): 3 # write code here 4 if not n: 5 return -1 6 cycle = list(range(n)) 7 start = 0 8 while len(cycle) > 1: 9 toremove = (start + m - 1) % len(cycle) 10 cycle.pop(toremove) 11 start = toremove 12 return cycle[0]
2. 数组中重复的数字
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
解:
用 hashset 做。

1 class Solution: 2 # 这里要特别注意~找到任意重复的一个值并赋值到duplication[0] 3 # 函数返回True/False 4 def duplicate(self, numbers, duplication): 5 # write code here 6 if not numbers: 7 return False 8 hashset = set() 9 for num in numbers: 10 if num in hashset: 11 duplication[0] = num 12 return True 13 hashset.add(num) 14 return False
不用辅助空间,比较巧妙。因为要返回的是任意一个重复的数字,把当前序列当成是一个下标和下标对应值是相同的数组;
遍历数组,判断当前位 i 的值和下标是否相等:
1. 若相等,则遍历下一位;
2. 若不等,则将当前位置i上的元素和a[i]位置上的元素比较:若它们相等,则成功!若不等,则将它们两交换。换完之后a[i]位置上的值和它的下标是对应的,但i位置上的元素和下标并不一定对应;重复2.的操作直到当前位置i的值也为i
3. 将i向后移一位,再重复2.
注意,这样找到的并不是一定是第一个重复的数字

1 class Solution: 2 # 这里要特别注意~找到任意重复的一个值并赋值到duplication[0] 3 # 函数返回True/False 4 def duplicate(self, numbers, duplication): 5 # write code here 6 if not numbers: 7 return False 8 # 判断数组元素是否都在0~n-1 9 n = len(numbers) 10 for i in range(n): 11 if numbers[i] < 0 or numbers[i] > n-1: 12 return False 13 14 for i in range(n): 15 while i != numbers[i]: 16 if numbers[i] == numbers[numbers[i]]: 17 duplication[0] = numbers[i] 18 return True 19 tmp = numbers[i] 20 numbers[i] = numbers[numbers[i]] 21 numbers[tmp] = tmp 22 return False
3. 构建乘积数组
给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。
解:
这题思路还是比较巧妙的,看个图就懂了。先算下三角的连乘,然后倒过来把剩下那部分也乘进去。
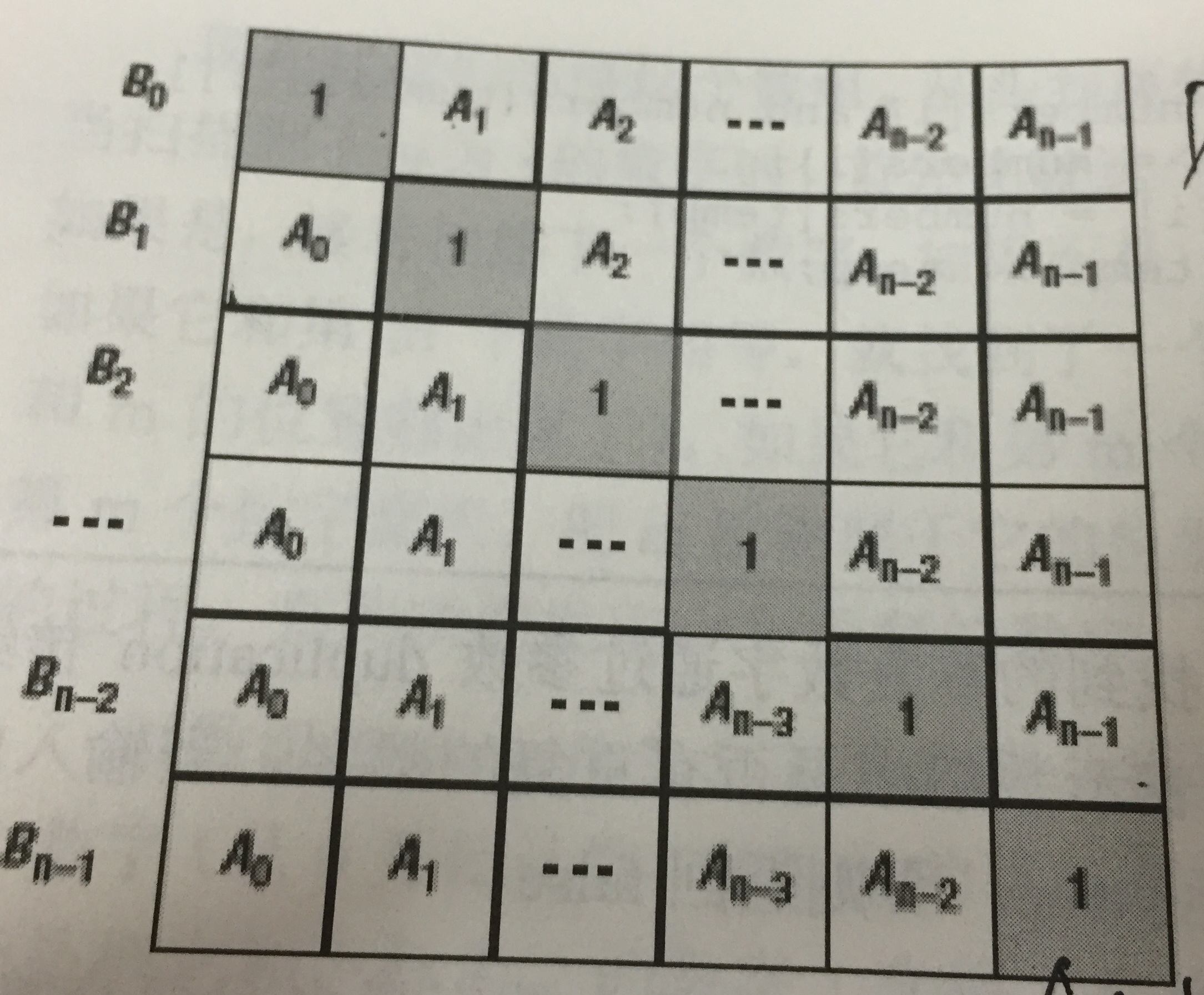

1 class Solution: 2 def multiply(self, A): 3 if not A: 4 return [] 5 n = len(A) 6 B_left = [1]*n 7 B_right = [1]*n 8 for i in range(1, n): 9 B_left[i] = B_left[i-1]*A[i-1] 10 B_right[-i-1] = B_right[-i]*A[-i] 11 for i in range(n): 12 B_left[i] *= B_right[i] 13 return B_left
4. 二维数组中的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
解:
第一种思路,能保证每一行都是有序的,按行二分查找。

1 class Solution: 2 # array 二维列表 3 def Find(self, target, array): 4 # write code here 5 if not array: 6 return False 7 m, n = len(array), len(array[0]) 8 9 def binarySearch(target, nums): 10 if not nums: 11 return False 12 left, right = 0, len(nums)-1 13 while left <= right: 14 mid = left + (right-left)//2 15 if nums[mid] == target: 16 return True 17 elif nums[mid] > target: 18 right = mid - 1 19 else: 20 left = mid + 1 21 return False 22 23 for i in range(m): 24 if binarySearch(target, array[i]): 25 return True 26 return False
另一种思路,考虑到左下角的元素,往右更大,往上更小。以左下角为起点搜索,如果比target大就向上,如果比target小就向右

1 class Solution: 2 # array 二维列表 3 def Find(self, target, array): 4 # write code here 5 if not array: 6 return False 7 m, n = len(array), len(array[0]) 8 i, j = m-1, 0 9 while i >= 0 and j < n: 10 if array[i][j] == target: 11 return True 12 elif array[i][j] > target: 13 i -= 1 14 else: 15 j += 1 16 return False
5. 连续子数组的最大和
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
解:
这题其实是个基础的dp问题,定义dp[i]表示以a[i]结尾的连续子向量最大和,那么显然dp[i] = max(dp[i-1] + array[i], array[i]),即如果以a[i-1]结尾的连续子向量最大和为正就保留,否则没有在做正贡献,直接从a[i]重新开始。
最后要求的是最大连续子序列的和,可能是以数组中任意位置元素结尾的,所以返回max(dp)

1 class Solution: 2 def FindGreatestSumOfSubArray(self, array): 3 if array is None or len(array)==0: 4 return 5 n = len(array) 6 dp = [0]*n 7 dp[0] = array[0] 8 for i in range(1, n): 9 dp[i] = max(dp[i-1] + array[i], array[i]) 10 return max(dp)
把空间效率再优化下

1 class Solution: 2 def FindGreatestSumOfSubArray(self, array): 3 if not array: 4 return 0 5 res = float('-inf') 6 n = len(array) 7 sum_ = array[0] 8 for i in range(1, n): 9 if sum_ > 0: 10 sum_ += array[i] 11 else: 12 sum_ = array[i] 13 res = max(res, sum_) 14 return res
6. 最小的k个数
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
解:
直接快排然后取前k个,O(NlogN)。但是N很大k很小的情况下这样很不划算。

1 class Solution: 2 def GetLeastNumbers_Solution(self, tinput, k): 3 # write code here 4 if not tinput or k > len(tinput): 5 return [] 6 tinput.sort() 7 return tinput[:k]
用小顶堆实现始终维护最小的K个数,O(NlogK)

1 import heapq 2 3 class Solution: 4 def GetLeastNumbers_Solution(self, tinput, k): 5 # write code here 6 if not tinput or k > len(tinput): 7 return [] 8 n = len(tinput) 9 heap =[] 10 for i in range(n): 11 heapq.heappush(heap, -tinput[i]) 12 if i >= k: 13 heapq.heappop(heap) 14 res = list(map(lambda x: -x, list(heap))) 15 res.sort() # 输出要求 16 return res
7. 和为 S 的连续正整数序列
小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!
输出描述:
输出所有和为S的连续正数序列。序列内按照从小至大的顺序,序列间按照开始数字从小到大的顺序
解:
这题思路还比较巧妙,双指针维护动态窗口,窗口内的和可以用等差数列通项公式计算。如果窗口内数字之和小于目标值,右游标右移(想让窗口和变大);小于目标值,左游标右移(拿掉一个窗口中最小的数)。如果找到一组解,左游标

1 class Solution: 2 def FindContinuousSequence(self, tsum): 3 # write code here 4 if tsum < 3: 5 return [] 6 res = [] 7 l, r = 1, 2 8 target = 2 * tsum 9 while l < r: 10 window = (l+r)*(r-l+1) 11 if window == target: 12 res.append(list(range(l, r+1))) 13 l += 1 14 elif window < target: 15 r += 1 16 else: 17 l += 1 18 return res
8. 数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数。
解:
二分查找 target 的左侧边界,再二分查找右侧边界,求区间长度即可

1 class Solution: 2 def GetNumberOfK(self, data, k): 3 # write code here 4 start = self.search(data, k) 5 if start == -1: 6 return 0 7 end = self.searchEnd(data, k) 8 return end - start +1 9 10 def search(self, nums, target): 11 if nums == None or len(nums) == 0: 12 return -1 13 low = 0 14 high = len(nums) 15 while low < high: 16 mid = (low + high) // 2 17 if nums[mid] == target: 18 high = mid 19 elif nums[mid] > target: 20 high = mid 21 elif nums[mid] < target: 22 low = mid + 1 23 if low == len(nums): 24 return -1 25 return low if nums[low] == target else -1 26 27 def searchEnd(self, nums, target): 28 if nums == None or len(nums) == 0: 29 return -1 30 low = 0 31 high = len(nums) 32 while low < high: 33 mid = (low + high) // 2 34 if nums[mid] == target: 35 low = mid + 1 36 elif nums[mid] > target: 37 high = mid 38 elif nums[mid] < target: 39 low = mid + 1 40 if low == len(nums)+1: 41 return -1 42 return low-1 if nums[low-1] == target else -1
9. 数组中只出现一次的数字
一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
解:
用哈希表统计出现次数

1 class Solution: 2 # 返回[a,b] 其中ab是出现一次的两个数字 3 def FindNumsAppearOnce(self, array): 4 # write code here 5 hashmap = dict() 6 for num in array: 7 hashmap[num] = hashmap.get(num, 0) + 1 8 9 res = [] 10 for key, value in hashmap.items(): 11 if value == 1: 12 res.append(key) 13 return res
假设只出现一次的两个数是A 和 B全部异或一次,结果就是 A、B的异或。找到A和B不同的位数,并以此为基准把原数组分成两部分,各自异或就行了

1 class Solution: 2 # 返回[a,b] 其中ab是出现一次的两个数字 3 def FindNumsAppearOnce(self, array): 4 # write code here 5 if not array: 6 return [] 7 resXor = 0 8 for num in array: 9 resXor ^= num 10 11 indicator = resXor & (-resXor) 12 13 num1, num2 = 0, 0 14 for num in array: 15 if num & indicator == 0: 16 num1 ^= num 17 else: 18 num2 ^= num 19 return [num1, num2]
10. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字
例如,如果输入如下4 X 4矩阵:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
解:
每一圈都是一样的,只要搞清楚每一圈的起点就行了。首先需要判断每一步开始是的坐标点是否满足小于行数的一半且小于列数的一半,在最后一圈中,可能出现仅能向右走一行,仅能向右走一行向下走一列,向右走一行向下走一列向左走一行,能走完整一圈,一共四种情况。其中只有能向右走一行必然发生,不必判断,剩余的都需要判断发生条件。

1 class Solution: 2 # matrix类型为二维列表,需要返回列表 3 def printMatrix(self, matrix): 4 # write code here 5 if not matrix: 6 return [] 7 rows, cols = len(matrix), len(matrix[0]) 8 start = 0 9 res = [] 10 while 2*start < rows and 2*start < cols: 11 res += self.printCycle(matrix, rows, cols, start) 12 start += 1 13 return res 14 def printCycle(self, matrix, rows, cols, start): 15 endx = cols - 1 - start 16 endy = rows - 1 - start 17 res = [] 18 # 从左到右 19 for i in range(start, endx+1): 20 res.append(matrix[start][i]) 21 # 从上到下 22 if start < endy: 23 for i in range(start+1, endy+1): 24 res.append(matrix[i][endx]) 25 # 从右到左 26 if start < endx and start < endy: 27 for i in range(endx-1, start-1, -1): 28 res.append(matrix[endy][i]) 29 # 从下到上 30 if start < endx and start < endy-1: 31 for i in range(endy-1, start, -1): 32 res.append(matrix[i][start]) 33 return res
11. 滑动窗口最大值
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
解:
用双端队列维护一个单调队列,window保存当前窗口中数的下标,window新的头总是当前窗口中最大的那个数。处理前 k 个元素,初始化window。遍历整个数组。在每一步清理双向队列:
只保留当前滑动窗口中有的元素的索引(因为滑动出去一个,要看一下window中的索引是不是都在i-k到i);
移除比当前元素小的所有元素,它们不可能是最大的;
将当前元素添加到双向队列中;
将 deque[0] 添加到输出中。

1 class Solution: 2 def maxInWindows(self, num, size): 3 # write code here 4 if not num or not size: 5 return [] 6 res = [] 7 n = len(num) 8 window = [] # 存窗口元素的索引 9 for i in range(n): 10 if i >= size and window[0] <= i-size: 11 window.pop(0) 12 while window and num[window[-1]] <= num[i]: 13 window.pop() 14 window.append(i) 15 if i >= size-1: 16 res.append(num[window[0]]) 17 return res
动态规划,将n个数据分成大小为k的块,定义left[i]为i所处的块的开始位置到i位置的最大值,right[j]为j所处的块的结束位置到j的最大值。那么滑动窗口就两种情况,要么没有跨越两个块,要么跨越了两个块。不管哪种情况,窗口从i到j,窗口最大值为max( right[i], left[j] )

1 class Solution: 2 def maxInWindows(self, num, size): 3 # write code here 4 if not num or not size: 5 return [] 6 n = len(num) 7 left, right = [0]*n, [0]*n 8 left[0], right[-1] = num[0], num[-1] 9 for i in range(1, n): 10 if i%size == 0: 11 left[i] = num[i] 12 else: 13 left[i] = max(left[i-1], num[i]) 14 15 j = n - 1 - i 16 if (j+1)%size == 0: 17 right[j] = num[j] 18 else: 19 right[j] = max(right[j+1], num[j]) 20 dp = [] 21 for i in range(n-size+1): 22 dp.append(max(right[i], left[i+size-1])) 23 return dp
12. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
解:
类二分的方法,不断的收缩两端边界。当然要先判断是否旋转了。

1 class Solution: 2 def minNumberInRotateArray(self, rotateArray): 3 # write code here 4 if not rotateArray: 5 return 0 6 if len(rotateArray)==1 or rotateArray[0] < rotateArray[-1]: 7 return rotateArray[0] 8 9 n = len(rotateArray) 10 left, right = 0, n-1 11 while left < right: 12 mid = left + (right-left)//2 13 if rotateArray[mid] > rotateArray[right]: # 最小数字一定在mid右边 14 left = mid + 1 # 左闭右开 15 elif rotateArray[mid] < rotateArray[right]: # 最小数字一定在mid左边 16 right = mid 17 else: # 不好判断是在mid左边还是右边,一个一个试 18 right -= 1 19 return rotateArray[right]
13.丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
解:

1 class Solution: 2 def GetUglyNumber_Solution(self, index): 3 # write code here 4 if index < 7: 5 return index 6 p2, p3, p5 = 0, 0, 0 7 arr = [0]*index 8 arr[0] = 1 9 for i in range(1, index): 10 arr[i] = min(arr[p2]*2, arr[p3]*3, arr[p5]*5) 11 # 三个if可能进入一个或多个 12 if arr[i] == arr[p2]*2: # 如果选了乘以2的队列,更新队头指针 13 p2 += 1 14 if arr[i] == arr[p3]*3: 15 p3 += 1 16 if arr[i] == arr[p5]*5: 17 p5 += 1 18 return arr[index-1]
维护一个堆,每次都把三个可能的丑数push进堆,但取出第i个丑数的时候,要保证取出之后堆顶是更大的丑数

1 import heapq 2 class Solution: 3 def GetUglyNumber_Solution(self, index): 4 # write code here 5 if index < 7: 6 return index 7 heap = [1] 8 for _ in range(index): 9 res = heapq.heappop(heap) 10 while heap and res == heap[0]: 11 res = heapq.heappop(heap) 12 q2, q3, q5 = res*2, res*3, res*5 13 for num in [q2, q3, q5]: 14 heapq.heappush(heap, num) 15 return res

1 # class ListNode: 2 # def __init__(self, x): 3 # self.val = x 4 # self.next = None 5 class Solution: 6 def FindFirstCommonNode(self, pHead1, pHead2): 7 # write code here 8 if not pHead1 or not pHead2: 9 return None 10 linkedList1Nodes = set() 11 p = pHead1 12 while p: 13 linkedList1Nodes.add(p) 14 p = p.next 15 16 p = pHead2 17 while p: 18 if p in linkedList1Nodes: 19 return p 20 p = p.next 21 return None
如果两个链表有公共节点,那么肯定会各自在某个节点处开始链向同一个节点。假设链表1长度为a+n,链表2长度为b+n,同时出发,p1到达链表1尾部的时候p2走到链表2的a+n处。这时p1再从链表2头部开始,当p2到达尾部时,p1处在链表2的b-a处。将p2从链表1头部开始,如果有公共节点,那么都再走a步就到达公共节点,否则都走a+n步到尾部。
代码及其简洁

1 # class ListNode: 2 # def __init__(self, x): 3 # self.val = x 4 # self.next = None 5 class Solution: 6 def FindFirstCommonNode(self, pHead1, pHead2): 7 # write code here 8 if not pHead1 or not pHead2: 9 return None 10 p1, p2 = pHead1, pHead2 11 while p1 != p2: 12 p1 = p1.next if p1 else pHead2 13 p2 = p2.next if p2 else pHead1 14 return p1
15. 数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
解:
归并排序的变式。先分成最低单位,考虑比较相邻的数字,再合并。合并过程中,出现前面的数组值array[i]大于后面数组值array[j]时;则前面数组array[i]~array[mid]都是大于array[j]的,count += mid+1 - i。例如5大于4, 那么5,7都会大于4,逆序对个数增加2
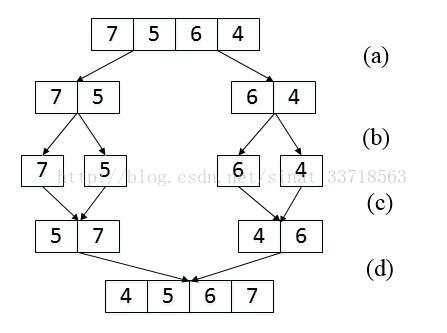

1 class Solution: 2 def __init__(self): 3 self.count = 0 4 5 def InversePairs(self, data): 6 # write code here 7 if not data: 8 return 0%1000000007 9 self.mergeSort(data) 10 return self.count%1000000007 11 12 def mergeSort(self, array): 13 if len(array) <= 1: 14 return array 15 num = len(array) // 2 16 left = self.mergeSort(array[:num]) 17 right = self.mergeSort(array[num:]) 18 # merge 19 l, r = 0, 0 20 result = [] 21 while l<len(left) and r<len(right): 22 if left[l] < right[r]: 23 result.append(left[l]) 24 l += 1 25 else: 26 result.append(right[r]) 27 r += 1 28 # 前面的array[i]大于后面的array[j]时,array[i]~array[mid]都比array[j]大,统计逆序对 29 self.count += len(left) - l 30 if l < len(left): 31 result += left[l:] 32 elif r < len(right): 33 result += right[r:] 34 return result
16.数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
解:
快排取中间位置的数,再遍历一遍统计个数判断,O(NlogN)
哈希表统计,线性复杂度,但需要额外空间

1 from collections import Counter 2 class Solution: 3 def MoreThanHalfNum_Solution(self, numbers): 4 # write code here 5 if not numbers: 6 return 0 7 n = len(numbers) 8 count = Counter(numbers) 9 for k, v in count.items(): 10 if v > n//2: 11 return k 12 return 0

1 class Solution: 2 def MoreThanHalfNum_Solution(self, numbers): 3 # write code here 4 if not numbers: 5 return 0 6 n = len(numbers) 7 res = numbers[0] 8 count = 1 9 for i in range(n): 10 if count == 0: 11 res = numbers[i] # 更新res为当前元素(新取两个数,看看是否相同) 12 count = 1 13 elif numbers[i] == res: 14 count += 1 # 相同则计数+1 15 else: 16 count -= 1 # 不同则计数-1(去掉两个不同的数) 17 18 count = 0 19 for i in range(n): 20 if numbers[i] == res: 21 count += 1 22 return res if count > n//2 else 0
