Vivado_HLS 学习笔记4-嵌套的循环的优化

优化的原理

HLS会自动尝试最小化循环的延迟. 除了这些自动的优化之外,directive文件负责

• 执行并行任务; 例如相同函数的多次执行,以及相同循环的多次迭代. 要进行pipeline设计;
• 重新设计数组(Block arrays),函数,循环和端口等的物理实现,改善数据的访存;
• 提供数据依赖的信息;

最终的优化手段是修改C源代码以移除非必要的数据依赖.

参考ug871的第7章.

对有数据依赖的计算如何优化设计

void matrixmul(
      mat_a_t a[MAT_A_ROWS][MAT_A_COLS],
      mat_b_t b[MAT_B_ROWS][MAT_B_COLS],
      result_t res[MAT_A_ROWS][MAT_B_COLS])
{
  // Iterate over the rows of the A matrix
   Row: for(int i = 0; i < MAT_A_ROWS; i++) {
      // Iterate over the columns of the B matrix
      Col: for(int j = 0; j < MAT_B_COLS; j++) {
         res[i][j] = 0;
         // Do the inner product of a row of A and col of B, 
         // 显然,内积的计算中,每次计算都需要读取上一次的res[i][j]并更新本次的res[i][j].存在同一循环不同迭代间的数据依赖.
         Product: for(int k = 0; k < MAT_B_ROWS; k++) {
            res[i][j] += a[i][k] * b[k][j];
         }
      }
   }

}

解决步骤1-pipeline最底层loop,

• 操作: 设置留空II以initiaion interval 为1
• 结果: 当最底层的loop循环进行pipeline不能降低latency(运算一次数据需要的时钟周期数)和Interval(下一次输入数据需要等待的间隔,如果等于latency说明没有pipeline)时,查看console看一下是否有蓝色字体 **Unable to enforce a carried dependence constraint **,执行步骤2;

解决步骤2-pipeline上一层loop

• 操作: 选择其上一层loop进行pipeline,而不是最底层pipeline.
• 如果发现并没有获得想要的结果,再次查看console的warnning!,发现Unable to schedule 'load' operation ('a_load_1', matrixmul.cpp:60) on array 'a' due to limited memory ports. Please consider using a memory core with more ports or partitioning the array 'a'.;

解决步骤3-数组分块(并行,需要多个端口并行)或reshape(需要一个更宽的端口)

• 操作1: 本例中,需要将数组a的[k]维度也就是第2维进行展开,数组 a -> Directive -> ARRAY_RESHAPE, dimension:2
• 操作2: 本例中,需要对数组b的[k]维度也就是第1维进行展开;数组 a -> Directive -> ARRAY_RESHAPE, dimension:1
• 结果: 能够看到II已经是1,满足了流水的设计要求;

解决步骤4-尝试添加FIFO接口

• 操作: 对输入端口a,b,和输出端口res设置-> Directive -> Interface ,ap_fifo
• 结果: console显示错误Port 'res' (matrixmul.cpp:48) of function 'matrixmul' cannot be set to a FIFO [SYNCHK 200-91] as it has both write (matrixmul.cpp:60:13) and read (matrixmul.cpp:60:13) operations.
• 分析: 在57行和60行等,对res[0][0]进行了多次连续的写操作,不满足stream的状况.这不是stream而是random access.
• 结果: 这种情况不能使用FIFO!

解决步骤5-继续优化!修改C代码

在重写C代码之前,需要对数组a,b,的访存地址进行分析:

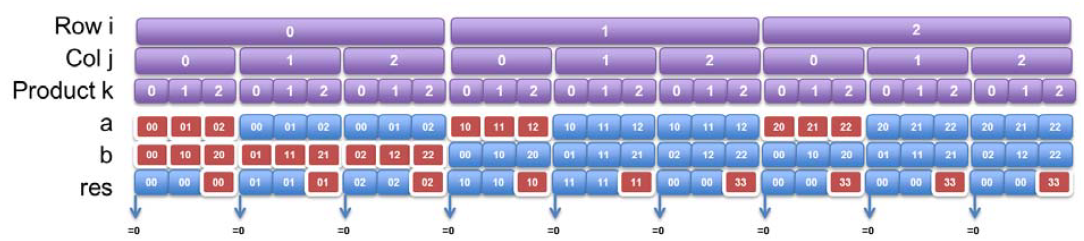
• 为了实现序列的流访存,端口只能在图中红色高亮的部分访存;
• 对于数组a,b的其他蓝色的读数据口,需要使用内部缓存cached获取;
• 对于输出res的其他端口,只能通过临时变量进行缓存,最终在红色时输出.

因此,改写后的代码为:

void matrixmul(
      mat_a_t a[MAT_A_ROWS][MAT_A_COLS],
      mat_b_t b[MAT_B_ROWS][MAT_B_COLS],
      result_t res[MAT_A_ROWS][MAT_B_COLS])
{
#pragma HLS ARRAY_RESHAPE variable=b complete dim=1
#pragma HLS ARRAY_RESHAPE variable=a complete dim=2
#pragma HLS INTERFACE ap_fifo port=a
#pragma HLS INTERFACE ap_fifo port=b
#pragma HLS INTERFACE ap_fifo port=res
  mat_a_t a_row[MAT_A_ROWS];
  mat_b_t b_copy[MAT_B_ROWS][MAT_B_COLS];
  int tmp = 0;

  // Iterate over the rowa of the A matrix
  Row: for(int i = 0; i < MAT_A_ROWS; i++) {
    // Iterate over the columns of the B matrix
    Col: for(int j = 0; j < MAT_B_COLS; j++) {
#pragma HLS PIPELINE rewind
      // Do the inner product of a row of A and col of B
      tmp=0;
      // Cache each row (so it's only read once per function)
      if (j == 0)
        Cache_Row: for(int k = 0; k < MAT_A_ROWS; k++)
          a_row[k] = a[i][k];
      
       // Cache all cols (so they are only read once per function)
     if (i == 0)
            Cache_Col: for(int k = 0; k < MAT_B_ROWS; k++)
               b_copy[k][j] = b[k][j];

      Product: for(int k = 0; k < MAT_B_ROWS; k++) {
        tmp += a_row[k] * b_copy[k][j];
      }
      res[i][j] = tmp;
    }
  }
}

注意事项

如果没有pipling loops,那么每计算一个数字,需要interval,计算tripcount次,就需要tripcount * interval;
pipling loops把循环的latency从$$Latency = iteration latency * tripcount $$ 变成了 $$Latency = iteration latency + (tripcount * interval)$$.

• loop的latency是指循环执行完成一次需要的时钟数;
• iteration latency是指循环内部单次执行完一次需要的时钟数;
• tripcount是指循环执行的次数.
• initiation interval是指本次数据输入和下次数据输入需要的间隔周期数.

---

注意: 对上层循环/模块的pipeline将导致对所有模块均进行pipeling,将展开所有循环.会极大地消耗资源.获得更高的吞吐量.