有两篇回答,我觉得都是正确的,从不同的方向来看的。
链接:https://www.zhihu.com/question/19734616/answer/174098489
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
先说结论: 皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进, 皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进, 皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进.
楼主如果高中正常毕业, 参加过高考, 那么肯定会这么一个公式
cos<a, b> = a • b / |a|•|b|
假设a = (3, 1, 0), b = (2, -1, 2)
分子是a, b两个向量的内积, (3, 1, 0) • (2, -1, 2) = 3•2 + 1•(-1) + 0•2 = 5
分母是两个向量模(模指的是向量的长度)的乘积.
总之这个cos的计算不要太简单...高考一向这是送分题...
然后问题来了, 皮尔逊系数和这个cos啥关系...(不好意思借用了我们学校老师的课件...)
 皮尔森相关系数计算公式
皮尔森相关系数计算公式
其实皮尔逊系数就是cos计算之前两个向量都先进行中心化(centered)...就这么简单...
中心化的意思是说, 对每个向量, 我先计算所有元素的平均值avg, 然后向量中每个维度的值都减去这个avg, 得到的这个向量叫做被中心化的向量. 机器学习, 数据挖掘要计算向量余弦相似度的时候, 由于向量经常在某个维度上有数据的缺失, 预处理阶段都要对所有维度的数值进行中心化处理.
我们观察皮尔逊系数的公式:
分子部分: 每个向量的每个数字要先减掉向量各个数字的平均值, 这就是在中心化.
分母部分: 两个根号式子就是在做取模运算, 里面的所有的 r 也要减掉平均值, 其实也就是在做中心化.
note: 我其实是今天上推荐系统课, 讲相似性计算的时候才发现原来余弦计算和皮尔逊相关系数计算就是一个东西两个名字啊......气死我了...高中的时候我还是靠背公式解题的...逃....
================2017-11-15更新: 对余弦相似度和皮尔森相关系数的进一步认识================
余弦距离(余弦相似度), 计算的是两个向量在空间中的夹角大小, 值域为[-1, 1]: 1代表夹角为0°, 完全重叠/完全相似; -1代表夹角为180°, 完全相反方向/毫不相似.
余弦相似度的问题是: 其计算严格要求"两个向量必须所有维度上都有数值", 比如:
v1 = (1, 2, 4),
v2=(3, -1, null),
那么这两个向量由于v2中第三个维度有null, 无法进行计算.
然而, 实际我们做数据挖掘的过程中, 向量在某个维度的值常常是缺失的, 比如v2=(3, -1, null), v2数据采集或者保存中缺少一个维度的信息, 只有两个维度. 那么, 我们一个很朴素的想法就是, 我们在这个地方填充一个值, 不就满足了"两个向量必须所有维度上都有数值"的严格要求了吗? 填充值的时候, 我们一般这个向量已有数据的平均值, 所以v2填充后变成v2=(3, -1, 2), 接下来我们就可以计算cos<v1, v2>了.
而皮尔逊相关系数的思路是, 我把这些null的维度都填上0, 然后让所有其他维度减去这个向量各维度的平均值, 这样的操作叫作中心化. 中心化之后所有维度的平均值就是0了, 也满足进行余弦计算的要求. 然后再进行我们的余弦计算得到结果. 这样先中心化再余弦计得到的相关系数叫作皮尔逊相关系数.
所以, 从本质上, 皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进.
另外, 以movielens数据集计算两个用户之间相似度的协同过滤场景来说, 余弦相似度和皮尔逊相关系数所表现的都是在两个用户都有打分记录的那些特征维度下, 他们超过自身打分平均值的幅度是否接近. 如果各维度下的超出幅度都类似, 那么就是比较相似的.
链接:https://www.zhihu.com/question/19734616/answer/117730676
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
要理解Pearson相关系数,首先要理解协方差(Covariance),协方差是一个反映两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值,反之相反,公式如下:
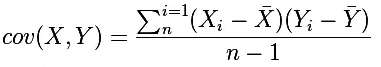
Pearson相关系数公式如下:
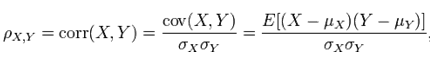
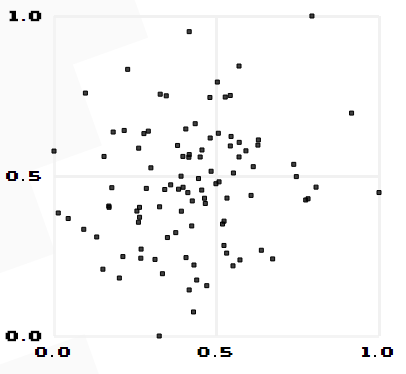
由公式可知,Pearson相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,例如,现在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的,如下图:
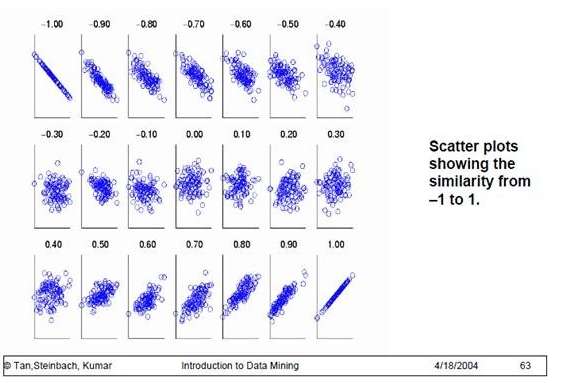
为了更好的度量两个随机变量的相关程度,引入了Pearson相关系数,其在协方差的基础上除以了两个随机变量的标准差,容易得出,pearson是一个介于-1和1之间的值,当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明: