很多题都是要求出什么最大公约数或者最小公倍数什么的,也有一些题目是和约数个数有关的,所以需要总结一下。
首先最大公约数和最小公倍数怎么求呢?
当然是观察法了,对于一些很聪明的孩纸他们一般随便一看就秒出答案,当然更聪明的孩纸知道最小公倍数并不容易求出。
所以需要先看出最大公约数,然后两数乘积/他们的最大公约数就是最小公倍数了。
我?我当然是上述方法求了。那样很快的。当然对于一些比较复杂的就要采取一些方法了。
如短除法,这样的方法实现很快的。
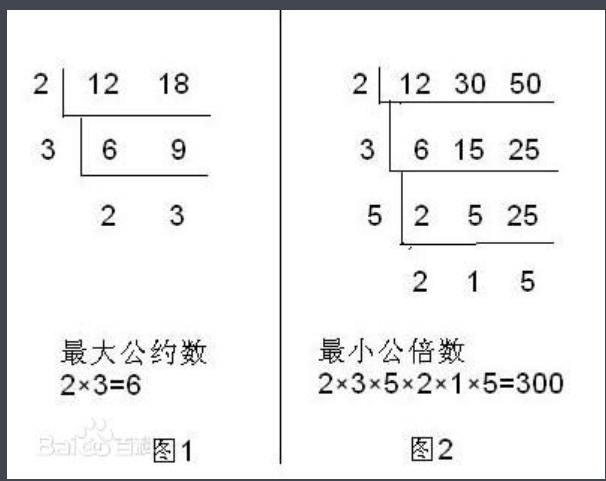
当求最大公约数的时候把列出的一个集合中的数字公共的约数全部除掉,最后左边一列数字的乘积即为答案,如图1。
很显然吧因为最大公约数就是每个数字中都能整除的数字且最大,所以他们公共的约数之积就是最大的公约数。
当求最小公倍数的时候呢?把这个集合任意几个(有的时候可能是1个)数字的约数除下,最后一圈数字相乘即为答案。如图2.。
这里由于下面是最根本的数字要相乘很显然,由于是最小公倍数,所以这个数字满足可以整除任何数字所以呢,由于每次都把一堆数字的存在的倍数都找出来,那么,这些数字相乘即为总体的倍数。原理其实就是把所有数字重复出现的质因数去掉,所有数字乘起来那这一定是最小公倍数了。说是显然其实也不过分。
这样就解决了求出最大公约数和最小公倍数的问题了。当然这个是针对多个数字求最大公约数和最小公倍数的了。
如果对于两个数字求最大公约数呢,换个名字gcd.那么就直接gcd了。
gcd(a,b)=gcd(b,a%b);(a>=b)
证明:设a=mc,b=nc;r=mc-knc=(m-kn)*c 因为 c|r 断定m-kn与n互质,则gcd(b,r)=c == gcd(a,b);
断定的话利用反正法法证明:设m-kn=xd,n=yd m-kn与n不互质有约数d 那么此时 a=(xd+kyd)c。b=ydc;显然a,b最大公约数为dc 不为c与原命题不相符。
因此c是b和r的最大公约数。证毕。
那么只要这样递归下去不断取%一定有b=0且此时最大公约数还在为c。得到答案。
当做高精gcd时就需要更相减损法了,因为%的高精不好写。
更相减损法:gcd(2a,2b)=gcd(a,b);gcd(a,b)=gcd(a,a-b)=gcd(b,a-b);
如果两个都为偶数那么除以2,互质则相减。这样最后a==b的时候最大公约数=2的乘积*等数。
证明:显然。
仔细想一下对于任意a,b的最大公约数d 都有d|a d|b 所以 d|(a-b);
所以在有限的次数中一定能得到等数这时就求出了最大公约数了...
写到这里我的头也比较懵吧,证明都看懂了,可最后求出的最大公约数还是不太懂,这可能需要时间沉淀吧,反正记住就行了;
约数个数:
对于一个整数n我们总能将其表示成n=p1^a1+p2^a2+...+pn^an;其中p为质因数
那么这样就很显然了约数个数=(a1+1)(a2+1)*...(an+1);因为a^0也算所以要加1;注意严谨。
约数和:
n的约数和=(p1^0+p1^1+...+p1^a1)(p2^0+...p2^a2)...(pn^0+pn^1+...pn^an);
证明:网上似乎没有证明,问学长学长说显然,我仔细看了一下发现是比较显然的吧。
仔细想发现是对的,但不知道为什么,时间来沉淀吧。