LINK:集合计数
容斥简单题 却引出我对广义容斥的深思。
一直以来我都不理解广义容斥是为什么 在什么情况下使用。
给一张图:
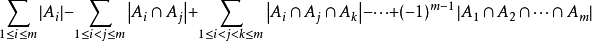
这张图想要表达的意思就是这道题目的意思 而求的东西也和题目一致。
特点:求出某个集合恰好为k的个数。
转换:求出集合>=k的个数或者<=k的个数 从而使用广义容斥容斥出来答案。
关于>=k个数 如上图可见 又很多重复的地方 而广义容斥也是在这么多重复的地方使用的 而并非严格>=k的个数。
换个说法 >=k的方案数 可能有一些存在重复 但是其特点是>=k 关于这个特点可以利用二进制的子集关系表现出来。
如 S1,S2都是恰好为k的 他们都能生成S3这个==k+1的集合 此时可以发现 S3被S1生成一次 被S2生成一次。所以所谓的>=k的方案数其中有一部分是子集的互相生成重复。
广义容斥就是利用这一点来计算的。
转到题目 不难发现 符合上面定义的>=k方案数为 (C(n,k)(2^{2^{n-k}}-1))
套广义容斥的式子即可求出答案 值得注意的是 (2^{n-k})可以由欧拉定理%(mod-1).
这道题还是一个简单容斥的类型。
可以发现所有的>=k的方案数为 (C(n,k)(2^{2^{n-k}}-1))
此时讨论 关于选出的k个子集固定时 此时生成的方案除掉这k个交集可能还存在其他交集 -1个交集+2个交集-...
这样套简单容斥的式子也行。值得注意的是这个讨论实在k个子集固定时的讨论。
广义容斥 code:
const ll MAXN=1000010,N=17;
ll n,k;
ll fac[MAXN],inv[MAXN];
inline ll ksm(ll b,ll p,ll pp)
{
ll cnt=1;
while(p)
{
if(p&1)cnt=cnt*b%pp;
b=b*b%pp;p=p>>1;
}
return cnt;
}
inline ll C(ll a,ll b){return a<b?0:fac[a]*inv[b]%mod*inv[a-b]%mod;}
signed main()
{
freopen("1.in","r",stdin);
get(n);get(k);fac[0]=1;
rep(1,n,i)fac[i]=fac[i-1]*i%mod;
inv[n]=ksm(fac[n],mod-2,mod);
fep(n-1,0,i)inv[i]=inv[i+1]*(i+1)%mod;
ll ans=0;
rep(k,n,i)
{
ans=(ans+(((i-k)&1)?-1:1)*(C(n,i)*(ksm(2,ksm(2,n-i,mod-1),mod)-1))%mod*C(i,k))%mod;
}
putl((ans+mod)%mod);
return 0;
}