欧拉函数

还是yyh dalao的带领下（其实是xjb学，随意点开一道题，其实是欧拉函数。学习了一下求法但不会证明（那就先不证明O(∩_∩)O

1~n中与N互质的数的个数被称之为欧拉函数，记作phi（N）；

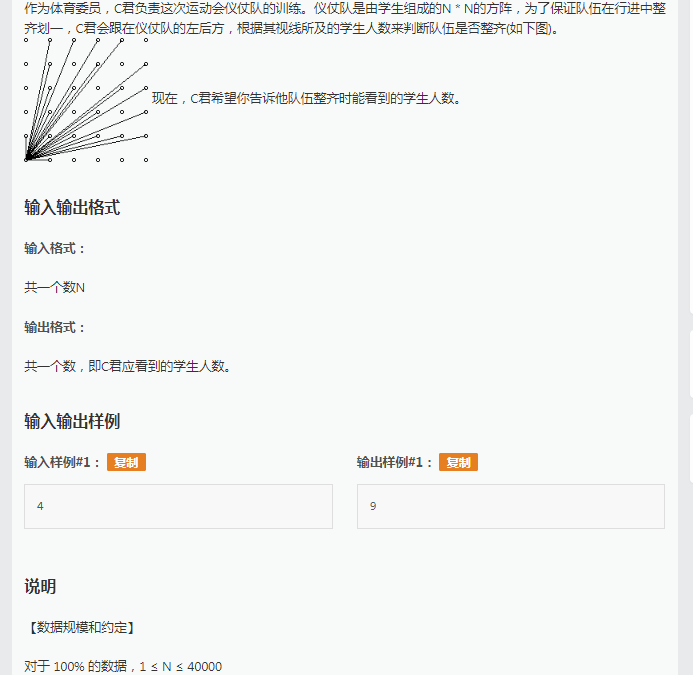
这道题仔细看其实就是一道裸的欧拉函数，关键就是求互质的长方形的个数，其实就是求2*从i-2到n的欧拉函数+3即可。

忘了说欧拉函数的求法：phi（n）=n/i*(i-1)其中i是1~n之间的质数。。

先考虑nsqrt（n）的做法暴力求，但注意这道题下标从1开始不是从0开始。

代码：

#include<iostream>
#include<string>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<ctime>
#include<vector>
#include<queue>
#include<map>
#include<stack>
using namespace std;
inline long long read()
{
    long long x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
long long n,ans=0;
long long phi(long long x)
{
    long long tmp=x;
    for(long long i=2;i*i<=x;i++)
    {
        if(x%i==0)tmp=tmp/i*(i-1);
        while(x%i==0)x=x/i;
    }
    if(x>1)tmp=tmp/x*(x-1);
    return tmp;
}
int main()
{
    long long n=read();
    for(long long i=3;i<=n;i++)
    {
        ans+=phi(i-1);
    }
    printf("%lld",ans*2+3);
    return 0;
}

还有一种类似于质数的爱拉斯托尼筛法，nloglogn级别的算法。其实跟筛质数的时候差不多，被我称之为非线性筛的线性筛法。。

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<iomanip>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<cstdio>
#define inf 100000000
using namespace std;
inline long long read()
{
    long long x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const long long maxn=40002;
long long m;
long long phi[maxn],ans=0;
void euler(long long n)
{
    for(long long i=2;i<=n;i++)phi[i]=i;
    for(long long i=2;i<=n;i++)
    if(phi[i]==i)for(long long j=i;j<=n;j+=i)
    phi[j]=phi[j]/i*(i-1);
}
int main()
{
    m=read();euler(m);
    if(m==1){printf("0
");return 0;}
    for(long long i=2;i<=m-1;i++)ans+=phi[i];
    printf("%lld
",ans*2+3);
    return 0;
}

还有一种是埃拉筛法，O（n）复杂度，线性筛。。这其实就和质数的线性筛差不多了在筛质数的同时进行欧拉函数的求解。

if(n%p^2==0)phi(n)=phi(n/p)*p;else phi(n)=phi(n/p)*(p-1);这其实就是求一个数的欧拉函数的话依靠一个质因数即可求解，当然本人不会证明短短的代码中有很深的学问。

代码：

#include<iostream>
#include<string>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<ctime>
#include<vector>
#include<queue>
#include<map>
#include<stack>
using namespace std;
inline long long read()
{
    long long x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const long long N=1e5+10;
long long p[N],n,m=0,phi[N],v[N],ans=0;
//p存储的是质数，v存储的是当前数字所含的最小质因子。
int main()
{
    n=read();
    for(long long i=2;i<=n;++i){
        if(!v[i]){
            v[i]=i;p[++m]=i;phi[i]=i-1;
        }
        for(long long j=1;j<=m;++j){
            if(v[i]<p[j]||p[j]*i>n) break;
            v[i*p[j]]=p[j];
            phi[p[j]*i]= phi[i]*(i%p[j]? p[j]-1 : p[j]);
        }
    }
    if(n==1){printf("0
");return 0;}
    for(long long i=1;i<=n-1;i++)ans+=phi[i];
    printf("%lld
",ans*2+3);
    return 0;
}

且放白鹿青崖间，须行即骑访名山！