基础概念
数据结构:是相互之间存在一种或多种关系的数据元素的集合。
逻辑结构和物理结构
关于数据结构,我们可以从逻辑结构和物理结构这两个维度去描述
逻辑结构是数据对象中数据元素之间的关系,是从逻辑意义上去描述的数据之间的组织形式。
逻辑结构有4种:
- 集合结构(数据元素之间仅以集合的方式体现,元素之间没有别的关系)
- 线性结构(数据元素之间存在一对一的关系)
- 树(数据元素之间为一对多或多对一的关系)
- 图(数据元素之间为多对多的关系)
物理结构则是逻辑结构在计算机中内存中的存储形式,分为两种:
- 顺序存储结构
- 链式存储结构
线性表(list)
线性表是零个或多个数据元素的的有限序列
线性表是线性结构,元素之间存在一对一的关系,线性表可通过顺序和链式两种方式来实现。
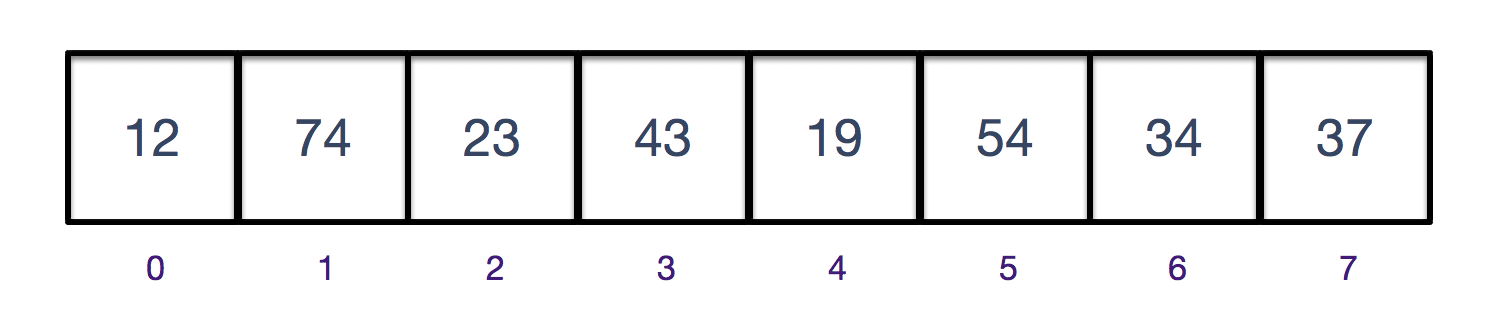
顺序存储结构,是用一段地址连续的存储单元依次存储线性表的数据元素
链式存储结构,用一组任意的存储单元来存储数据元素,不要求物理存储单元的连续性,由一系列结点组成,每个结点除了要存储数据外,还需存储指向后继结点或前驱结点的存储地址。

顺序存储和链式存储对比
- 顺序存储结构
- 优点
- 实现比较简单
- 查找指定位置的元素效率很快,时间复杂度为常数阶O(1)
- 无需额外存储元素之间的逻辑关系(链式存储由于存储空间随机分配,需要存储元素之间的逻辑关系)
- 缺点
- 需要预先分配存储空间,如果数据元素数量变化较大,很难确定存储容量,并导致空间浪费
- 若频繁进行插入删除操作,则可能需要频繁移动大量数据元素
- 优点
- 链式存储结构
- 优点
- 不需要提前分配存储空间,元素个数不受限制
- 对于插入删除操作,在已找到目标位置前提下,效率很高,仅需处理元素之间的引用关系,时间复杂度为O(1)
- 缺点
- 实现相对复杂
- 查找效率较低,最坏情况下需要遍历整张表
- 由于物理存储位置不固定,需要额外存储数据元素之间的逻辑关系
- 优点
链式存储代码实现
单链表
package listdemo; /** * Created by chengxiao on 2016/10/18. */ public class MyLinkedList { /** * 指向头结点的引用 */ private Node first ; /** * 线性表大小 */ private int size; /** * 结点类 */ private static class Node{ //数据域 private int data; //指向后继结点的引用 private Node next; Node(int data){ this.data = data; } } /** * 从头部进行插入 * 步骤:1.新结点的next链指向当前头结点;2.将first指向新节点 * 时间复杂度:O(1) * @param data */ public void insertFirst(int data){ Node newNode = new Node(data); newNode.next = first; first = newNode; size++; } /** * 从头部进行删除操作 * 步骤:1.将头结点的next链置空 2.将first引用指向第二个结点 * 时间复杂度为:O(1) * @return */ public boolean deleteFirst(){ if(isEmpty()){ return false; } Node secondNode = first.next; first.next = null; first = secondNode; size--; return true; } /** * 取出第i个结点 * 步骤:从头结点进行遍历,取第i个结点 * 时间复杂度:O(n),此操作对于利用数组实现的顺序存储结构,仅需常数阶O(1)即可完成。 * @param index * @return */ public int get(int index) throws Exception { if(!checkIndex(index)){ throw new Exception("index不合法!"); } Node curr = first; for(int i=0;i<index;i++){ curr = curr.next; } return curr.data; } /** * 遍历线性表 * 时间复杂度:O(n) */ public void displayList(){ Node currNode = first; while (currNode!=null){ System.out.print(currNode.data+" "); currNode = currNode.next; } System.out.println(); } /** * 链表是否为空 * @return */ public boolean isEmpty(){ return first == null; } /** * index是否合法 * @param index * @return */ private boolean checkIndex(int index){ return index >= 0 && index < size; } /** * 链表大小 * @return */ public int size() { return size; } public static void main(String []args) throws Exception { MyLinkedList myLinkedList = new MyLinkedList(); //从头部插入 myLinkedList.insertFirst(1); myLinkedList.insertFirst(2); myLinkedList.insertFirst(3); myLinkedList.insertFirst(4); //遍历线性表中元素 myLinkedList.displayList(); //获取第二个元素 System.out.println(myLinkedList.get(2)); //删除结点 myLinkedList.deleteFirst(); myLinkedList.displayList(); } }
输出结果
4 3 2 1
2
3 2 1
双端链表
上面罗列了线性表中的几种基本操作,考虑下,如果要提供一个在链表尾部进行插入的操作insertLast,那么由于单链表只保留了指向头结点的应用first,需要从头结点不断通过其next链找后继结点来遍历,时间复杂度为O(n)。其实,我们可以在保留头结点引用的时候,也保留一个尾结点的引用。这样,在从尾部进行插入时就方便多了
双端链表同时保存对头结点和对尾结点的引用
/** * 指向头结点的引用 */ private Node first ; /** * 指向尾结点的引用 */ private Node rear;
从尾部进行插入
/** * 双端链表,从尾部进行插入 * 步骤:将当前尾结点的next链指向新节点即可 * 时间复杂度:O(1) * @param data */ public void insertLast(int data){ Node newNode = new Node(data); if(isEmpty()){ first = newNode; rear = newNode; size++; return; } rear.next = newNode; rear = newNode; size++; }
做其他操作的时候也需注意保持对尾结点的引用,此处不再赘述。
双向链表
再考虑下,如果我们要提供一个删除尾结点的操作,步骤很简单:在删除尾结点的过程中需要将其前驱结点(即倒数第二个结点)的next链引用置为空,但由于我们的链表是单链表,一条道走到黑,要找倒数第二个结点得从头开始遍历,这种情况下,我们就可以考虑使用双向链表。
双向链表的的每一个结点,包含两个指针域,一个指向它的前驱结点,一个指向它的后继结点。

/** * 删除尾结点 * 主要步骤:1.将rear指向倒数第二个结点 2.处理相关结点的引用链 * 时间复杂度:O(1) * @return */ public void deleteLast() throws Exception { if(isEmpty()){ throw new Exception("链表为空"); } Node secondLast = rear.prev; rear.prev = null; rear = secondLast; if(rear == null){ first = null; }else{ rear.next = null; } size--; }
其他操作同理,在过程中需要同时保持对结点的前驱结点和后继结点的引用,删除操作时,需要注意解除废弃结点的各种引用,便于GC。
总结
本文对数据结构的一些基本概念,逻辑结构和物理结构,线性表等概念进行了基本的阐述。同时,介绍了线性表的顺序存储结构和链式存储结构,对线性表的链式存储结构(单链表,双端链表,双向链表),使用Java语言做了基本实现。数据结构的重要性毋庸置疑,它是软件设计的基石,由于自己非科班出身,虽曾自学过一段时间,也不够系统,最近希望能重新系统地梳理下,本篇就当自己数据结构再学习的开篇吧,共勉。