数据结构：二叉数查找树基本实现

1.写在前面

　　二叉查找树得以广泛应用的一个重要原因是它能保持键的有序性，因此我们可以把它作为实现有序符号表API中的众多方法的基础。

　　也就是说我们构建较为完整的二叉查找树API，为以后作为有序符号表提供基础。

　　二叉查找树是高效的，灵活的。

　　.....

2.代码分解

2.1 找到最大键和最小键

　　既然是二叉查找树可以作为一个有序符号表，那么必然要提供获取最大键和最小键的功能。

    public Key min()
    {
        return min(root).key;
    }
    private Node min(Node root)
    {
        if(root.Left==null)　　//root.Right==null return 0
            return root;            //return max(root.Right);
        return min(root.Left);
    }

　　|说明：

　　　　1.简要思路，根据二叉树的结构，我们知道，一个节点左边相连的节点一定是较小的，所以最小节点一定在从根节点开始一直往左走的位置，知道遇到一个节点的左节点是NULL，我们边返回这个左节点。

　　　　2.递归的思路也比较简单，最大值的求法与最小值基本相同，注释已经标注。

2.2 向上取整和向下取整

    public Key floor(Key key)
    {
        return floor(root,key).key;
    }
    private Node floor(Node root,Key key)
    {

        if(root==null)
            return null;

        int cmp = key.compareTo(root.key);
        if(cmp==0)
            return root;　
        if(cmp<0)
            return  floor(root.Left,key);
        Node t =floor(root.Right,key);　／／每次往右边走我们都需要记录一下，分析看说明
        if(t!=null)
            return t;
        else
            return root;
    }

　　|说明：

　　　　

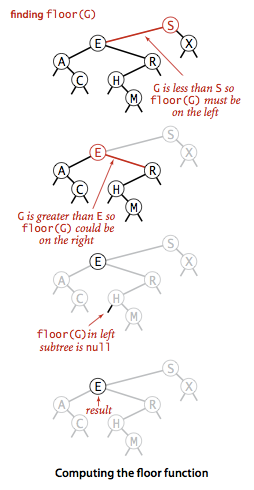
　　　　由上图我们来分析一下思路，找G元素，先比较G元素与S元素，很显然G元素<S元素，那么我们需要往左边走，因为向下取整的数（简计为floor）一定是小于等于它自己的。到了Ｅ元素，很显然我们G是大于Ｅ的，此时，我们需要记录Ｅ，因为它右边的元素都大于Ｅ，后面的元素都可能会更接近Ｇ，但也有可能大于Ｇ，所以我们记录它。然后我们往右边走，．．然后和Ｒ比，往左走，和Ｈ比往左走，此时发现Ｇ在Ｈ左侧的话是空值ＮＵＬＬ，所以对于floor来说取Ｅ最好。

2.3 根据K值选择节点（返回排名为K的键）

public Key select(int k)
    {
        return select(root,k).key;
    }

    public Node select(Node x,int k)
    {
        //返回排名为K的节点
        if(x==null)
            return null;
        int t =size(x.Left);  
        if(t>k)
            return select(x.Left,k);
        else if (t<k)
            return select(x.Right,k-t-1);
        else
            return x;
    }

　　|说明：

　　　　　　

2.4返回给定键的排名

public int rank(Key k){
        return rank(k,root);
    }
    public int rank(Key k,Node x)
    {
        if(x==null)
            return 0;
        int cmp=k.compareTo(x.key);

        if(cmp<0) return rank(k,x.Left);
        else if(cmp>0) return 1+rank(k,x.Right)+size(x.Left);
        else return size(x.Left);
    }