AVL树

AVL树

在二叉查找树（BST）中，频繁的插入操作可能会让树的性能发生退化，因此，需要加入一些平衡操作，使树的高度达到理想的O(logn)，这就是AVL树出现的背景。注意，AVL树的起名来源于两个发明者：Adel'son-Vel'skii 和 Landis。

AVL树除了具备BST树的基本特征之外，还具有一个非常重要的特点：

如果将一个节点的左、右子树的高度差定义为该节点的平衡因子，则AVL树的任意一个节点的平衡因子只有0、-1、1 三种取值。

可以采用递归的方法来判断一个BST树是不是AVL树：

typedef struct _pnode
{
    int data;
    int height;
    struct _pnode *left;
    struct _pnode *right;
} pnode;

static int TreeDepth (pnode p)
{
    if (!p) return 0;

    int nLeft = TreeDepth(p->left);
    int nRight = TreeDepth(p->right);

    return (nLeft > nRight) ? (nLeft+1) : (nRight+1);
}

static int IsBalanced(pnode root)
{
     if (NULL == root)
          return 1;

     int left = TreeDepth(root->left);
     int right = TreeDepth(root->right);

     int diff = left - right;

     if (diff > 1 || diff < -1) {
         return 0;
     }   

     return IsBalanced(root->left) && IsBalanced(root->right);
}

递归法的代码虽然简洁，但同一个结点会被重复遍历多次，因此效率并不高。

用后序遍历的方式遍历二叉树的每一个结点，在遍历到一个结点之前我们已经遍历了它的左右子树。
只要在遍历每个结点的同时记录它的深度，就可以一边遍历一边判断每个结点是否平衡。

static int IsBalanced2(pnode root, int* pDepth)
{
     int left, right;

     if (root == NULL) {
          *pDepth = 0;
          return 1;
     }   

     if (IsBalanced2(root->left, &left)
               && IsBalanced2(root->right, &right)) {

          int diff = left - right;
          if (diff <= 1 && diff >= -1) {
               *pDepth = 1 + (left > right ? left : right);
               return 1;
          }   
     }   

     return 0;
}

那么，AVL树是如何保证其平衡呢？当插入一个节点时，首先检查是否因插入而破坏了平衡，若破坏，则找出其中的最小不平衡子树，在保持二叉排序树特性的情况下，调整最小不平衡子树中节点之间的关系（通过左旋转和右旋转实现），以达到新的平衡。

注意：最小不平衡子树指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树。 

---

树的旋转

有四种情况可能导致二叉查找树不平衡，分别为：

• LL： 插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由1变为2
• LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由1变为2
• RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由-1变为-2
• RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由-1变为-2

 

如下图，是四种不平衡的情况：

 

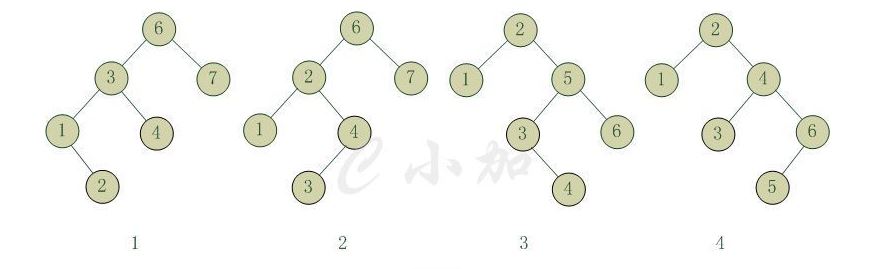
1和4两种情况是对称的，这两种情况的旋转算法是一致的，只需要经过一次旋转就可以达到目标，我们称之为单旋转。2和3两种情况也是对称的，这两种情况的旋转算法也是一致的，需要进行两次旋转，我们称之为双旋转。

 

单旋转是针对于LL和RR这两种情况的解决方案，这两种情况是对称的，只要解决了LL这种情况，RR就很好办了。

下图是LL情况的解决方案，节点k2不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的左子树X子树，所以属于LL情况。

 

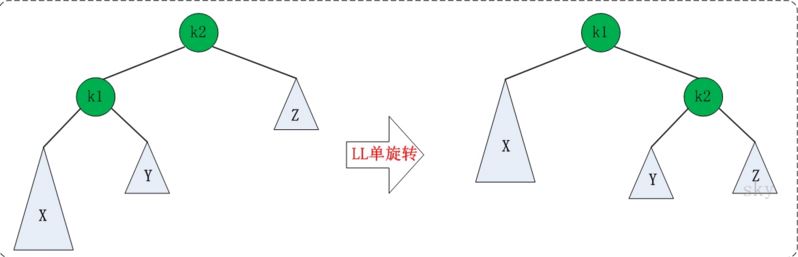
为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

这样的操作只需要一部分指针改变，结果我们得到另外一颗二叉查找树，它是一棵AVL树，因为X向上一移动了一层，Y还停留在原来的层面上，Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同，插入操作使得X高度长高了。因此，由于这颗子树高度没有变化，所以通往根节点的路径就不需要继续旋转了。

 

LL单旋转：

void SingRotateLeft(pnode* &k2)
{
    pnode *k1;

    k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2; 

    k2->height = Max(TreeDepth(k2->left), TreeDepth(k2->right)) + 1;
    k1->height = Max(TreeDepth(k1->left), k2->height) + 1;
}

RR单旋转类似，

 

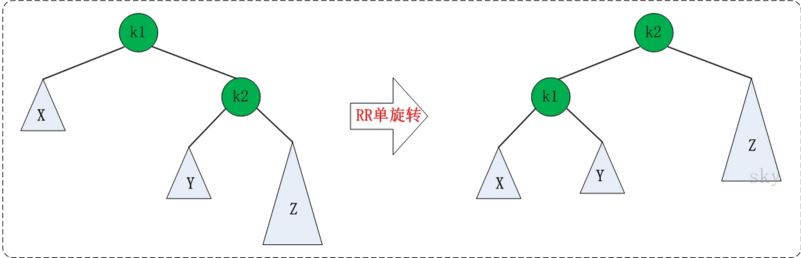
void SingRotateRight(pnode* &k2)
{
    pnode *k1;

    k1 = k2->right;
    k2->right = k1->left;
    k1->left = k2;

    k2->height = Max(TreeDepth(k2->left), TreeDepth(k2->right))+1;
    k1->height = Max(TreeDepth(k1->right), k2->height)+1;
}
~     

 

对于LR和RL这两种情况，单旋转不能使它达到一个平衡状态，要经过两次旋转。双旋转是针对于这两种情况的解决方案，同样的，这样两种情况也是对称的，只要解决了LR这种情况，RL就很好办了。

下图是LR情况的解决方案，节点k3不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的右子树k2子树，所以属于LR情况。

 

 

第一次旋转是围绕"k1"进行的"RR旋转"，第二次是围绕"k3"进行的"LL旋转"。

LR的旋转代码

void DoubleRotateLR(pnode* &k3)
{
    SingRotateRight(k3->left);
    SingRotateLeft(k3);
}

RL也是类似的，

void DoubleRotateRL(pnode* &k3)
{
    SingRotateLeft(k3->right);
    SingRotateRight(k3);
}

---

插入

插入的方法和二叉查找树基本一样，区别是，插入完成后需要从插入的节点开始维护一个到根节点的路径，每经过一个节点都要维持树的平衡。维持树的平衡要根据高度差的特点选择不同的旋转算法。

void insert(pnode* &node, int key)
{
    // 如果节点为空,就在此节点处加入key信息
    if (node == NULL) {   
        node = (pnode*) malloc(sizeof(pnode));
        memset(node, 0, sizeof(pnode));
        node->data = key;

    // 如果key小于节点的值,就继续在节点的左子树中插入key
    } else if (node->data > key) { 

        insert(node->left, key);

        // 如果高度之差为2的话就失去了平衡,需要旋转
        if (2 == TreeDepth(node->left) - TreeDepth(node->right)) {

            if (key < node->left->data) {
                SingRotateLeft(node);

            } else {
                DoubleRotateLR(node);
            }   
        }   

    //如果key大于节点的值,就继续在节点的右子树中插入key
    } else if (node->data < key) {    

        insert(node->right, key);

        if (2 == TreeDepth(node->right)-TreeDepth(node->left)) {

            if (key > node->right->data) {
                SingRotateRight(node);

            } else {
                DoubleRotateRL(node);
            }   
        }   

    } else {
        // 如果相等
        printf("error: key depulicated!");
    }   

    node->height = Max(TreeDepth(node->left), TreeDepth(node->right)) + 1;
}

---

删除