二叉堆
我们知道堆栈是一种LIFO(后进先出)结构,队列是一种FIFO(先进先出)结构,而二叉堆是一种最小值先出的数据结构,因此二叉堆很适合用来做排序。
二叉树的性质:二叉堆是一棵完全二叉树,且任意一个结点的键值总是小于或等于其子结点的键值,
二叉堆采用数组来存储(按广度优先遍历的顺序),而没有像普通的树结构使用指针来表示节点间的关系。
如下图所示:
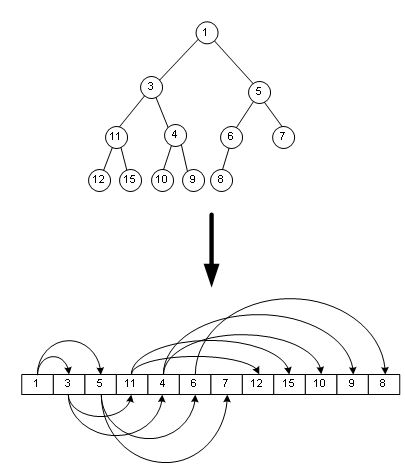
如图,最小的一个元素就是数组第一个元素。
将二叉堆按最广优先遍历的顺序编号从0到N-1,根据完全二叉树的性质,则第n个结点的子结点分别是2n+1和2n+2,其父结点是(n-1)/2。并且,叶子结点的下标是从 (N-1)/2开始,一直到N-1。这样,对于数组中的任意一个元素,我们可以很方便的计算出它的父节点、孩子节点所在的位置(即数组下标)。
插入
如果要在二叉堆中插入或删除一个元素,必须保证堆性质仍能满足。
新插入的节点new 放在完全二叉树最后的位置,再和父节点比较。如果new节点比父节点小,那么交换两者。交换之后,继续和新的父节点比较…… 直到new节点不比父节点小,或者new节点成为根节点。这样得到的树,就恢复了堆的性质。
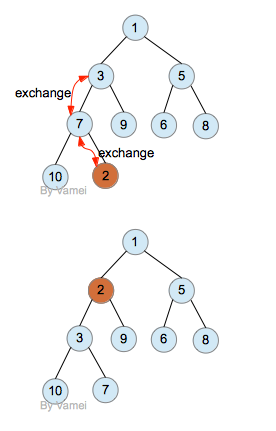
删除
删除操作一定是踢出数组的第一个元素(即根节点),这么来第一个元素以前的位置就成了空位,让最后一个节点 last成为新的节点,从而构成一个新的二叉树。再将last节点不断的和子节点比较。如果last节点比两个子节点中小的那一个大,则和该子节点交换。直到last节点不大于任一子节点都小,或者last节点成为叶节点。
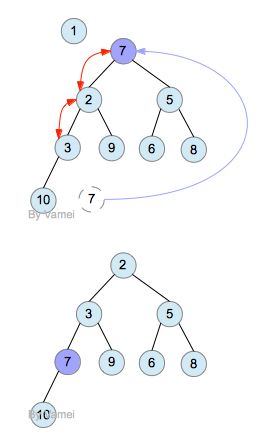
C代码实现:
插入操作:
void fix_up_min_heap( int arr[], int n, int len, int i ) // n 为数组容量,len为当前长度 { int j = ( i - 1 ) / 2; // parent index int tmp = arr[i]; while (j >= 0 && tmp < arr[j]) { arr[i] = arr[j]; i = j; if (j <= 0) break; j = ( j - 1 ) / 2; } arr[i] = tmp; } int insert_min_heap( int arr[], int n, int * len, int x ) { if( n == *len ) return -1; arr[(*len)++] = x; fix_up_min_heap( arr, n, *len, *len - 1 ); return 1; }
删除操作:
void fix_down_min_heap( int arr[], int n, int len, int i ) { int j = 2 * i + 1; int tmp = arr[i]; while( j < len ) { if( j < len - 1 && arr[j + 1] < arr[j] ) ++j; if( arr[j] < tmp ) { arr[i] = arr[j]; i = j; j = 2 * i + 1; } else { break; } } arr[i] = tmp; } void pop_min_heap( int arr[], int n, int * len ) { if( *len <= 0 ) return; arr[0] = arr[--*len]; fix_down_min_heap( arr, n, *len, 0 ); }
最小堆和最大堆
最大堆:父结点的键值总是大于或等于任何一个子结点的键值;最大堆常用于排序算法。
最小堆:父结点的键值总是小于或等于任何一个子结点的键值;最小堆常用于优先队列。
堆的意义就在于:最快的找到最大/最小值,在堆结构中插入一个值重新构造堆结构,取走最大/最下值后重新构造堆结构;其时间复杂度为O(logN);
堆实践中用途不在于排序,其主要用在调度算法中,比如优先级调度,每次取优先级最高的,时间驱动,取时间最小/等待最长的 等等 ,分为最大堆/最小堆。
利用最大堆和最小堆可以求一个包含N个元素的数组的前K大(或小)的数,原理如下:
我们首先取这N个元素中的前K个元素来建立一个由K个元素组成的小(大)顶堆,这样堆顶元素便是当前已读取元素中的第K大(小)者;然后,依次读取剩下的N-K个元素,而对于其中的每个元素x,若x大于(小于)当前的堆顶元素,则将堆顶元素替换为x,并自堆顶至向下调整堆;这样,在读取完所有元素后,堆中的K个元素即为这N个数中的前K个最大(小)元素,同时堆顶元素为这N个数中的第K大(小)元素。