旅行商问题
旅行商问题(TravelingSalesmanProblem,TSP)是一个经典的组合优化问题。经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列,随着顶点数的增加,会产生组合爆炸,它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用,国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题,常用的方法包括:分枝定界法、线性规划法、动态规划法等。但是,随着问题规模的增大,精确算法将变得无能为力,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。
DisMinGraph.java
1 package com.itheima.controller; 2 3 import java.util.ArrayList; 4 import java.util.Arrays; 5 import java.util.Scanner; 6 public class DisMinGraph { 7 static final int MaxValue=65535; //最大值(可设为一个最大整数) 8 static Scanner input=new Scanner(System.in); 9 10 public static void main(String[] args) { 11 GraphMatrix GM=new GraphMatrix(); //定义保存邻接表结构的图 12 System.out.printf("求解最短路径问题! "); 13 System.out.println("请输入图顶点数!"); 14 int VertexNum=input.nextInt(); 15 System.out.println("请输入图顶点数"); 16 int EdgeNum=input.nextInt(); //输入图边数 17 char[] points=new char[VertexNum]; //读取顶点信息 18 char[][] roads=new char[EdgeNum][2]; //读取边信息,起点和终点 19 int[] weight=new int[EdgeNum]; //读取边权重 20 System.out.println("请输入图论中的顶点符号:例如:C1,C2,C3,C4,C5"); 21 for(int i=0;i<points.length;i++){ 22 points[i]=(input.next().toCharArray())[0]; 23 } 24 System.out.println("请输入顶点 顶点 权值,例如:C1 C2 7"); 25 for(int i=0;i<roads.length;i++){ 26 roads[i][0]=(input.next().toCharArray())[0]; 27 roads[i][1]=(input.next().toCharArray())[0]; 28 weight[i]=input.nextInt(); 29 } 30 CreateGraph(GM,points,roads,weight); //生成邻接表结构的图 31 // OutGraph(GM); //输出邻接矩阵 32 System.out.println("请输入出发点!例如:C1"); 33 int vend=GM.indexOf((input.next().toCharArray())[0]); //获取出发点位置 34 if(vend==-1){ 35 System.out.println("顶点不存在,请重新输入!"); 36 return; 37 } 38 int[][] disMin=DistMin(GM,vend); //执行最小路径算法 39 System.out.println("各顶点到达顶点“"+GM.Vertex[vend]+"”的最短路径分别为(起始点 - 结束点):"); 40 int max=0; 41 String cc=""; 42 for(int i=0;i<GM.VertexNum;i++) //各个顶点到出发点的路径 43 { 44 char[][] path=getPath(GM,disMin,vend,i); 45 if(max<(int)path[1][0]){ 46 max=(int)path[1][0]; 47 cc= Arrays.toString(path[0]); 48 } 49 System.out.println("-->"+Arrays.toString(path[0])+"-------------->路径长度:"+(int)path[1][0]); 50 } 51 System.out.println("行最长路径的最短距离-->"+Arrays.toString(new String[]{cc})+"-------------->路径长度:"+max); 52 53 } 54 55 private static void CreateGraph(GraphMatrix GM,char[] points,char[][] roads,int[] weights){ //创建邻接矩阵图 56 GM.setVertex(points); 57 GM.setEdgeWeight(roads, weights); 58 } 59 /** 60 * 输出图的邻接矩阵 61 * @param GM 62 */ 63 public static void OutGraph(GraphMatrix GM) 64 { 65 int i,j; 66 System.out.print(" "); 67 for(i=0;i<GM.VertexNum;i++) 68 { 69 for(j=0;j<GM.VertexNum;j++) 70 { 71 if(GM.EdgeWeight[i][j]==MaxValue) //若权值为最大值 72 { 73 System.out.print(" Z"); //以Z表示无穷大 74 } 75 else 76 { 77 System.out.print(" "+GM.EdgeWeight[i][j]); //输出边的权值 78 } 79 } 80 System.out.print(" "); 81 } 82 } 83 84 private static int[][] DistMin(GraphMatrix GM,int vend) //最短路径算法 85 { 86 //可到达指定顶点(出发点)的顶点集合,下标表示顶点位置,值表示是否可以到达,0表示不能,1表示能 87 int[] tmpvertex=new int[GM.VertexNum]; 88 //从所有顶点到达指定顶点(出发点)的路径索引数组;下标为对应顶点,值为对应顶点可到达的下一个顶点 89 int[] path=new int[GM.VertexNum]; 90 int[] weight=new int[GM.VertexNum]; //某终止点到各顶点的最短路径长度 91 for(int i=0;i<GM.VertexNum;i++) //初始weight数组 92 { 93 tmpvertex[i]=0; //初始化顶点集合为空 94 weight[i]=GM.EdgeWeight[vend][i]; //保存最小权值 95 if(weight[i]<MaxValue && weight[i]>0) //有效权值 96 { 97 path[i]=vend; //保存边 98 } 99 } 100 tmpvertex[vend]=1; //选入顶点vend 101 weight[vend]=0; 102 for(int i=0;i<GM.VertexNum;i++) 103 { 104 int min=MaxValue; 105 int k=vend; 106 for(int j=0;j<GM.VertexNum;j++) //查找未用顶点的最小权值 107 { 108 if(tmpvertex[j]==0 && weight[j]<min) 109 { 110 min=weight[j]; 111 k=j; 112 } 113 } 114 tmpvertex[k]=1; //将顶点k选为可到达指定定点(出发点) 115 for(int j=0;j<GM.VertexNum;j++) //以顶点k为中间点,重新计算权值 ,判断是否有以顶点k为中继到达指定定点(出发点)权值更小的点 116 { 117 if(tmpvertex[j]==0 && weight[k]+GM.EdgeWeight[k][j]<weight[j]) 118 { 119 weight[j]=weight[k]+GM.EdgeWeight[k][j]; 120 path[j]=k; 121 } 122 } 123 } 124 return new int[][]{tmpvertex,path}; 125 } 126 127 public static char[][] getPath(GraphMatrix GM,int[][] disMin,int vend,int end){ 128 ArrayList<Character> path=new ArrayList<Character>(); 129 int l=0; 130 if(disMin[0][end]==1) 131 { 132 int k=end; 133 while(k!=vend) 134 { 135 path.add(GM.Vertex[k]); 136 l+=GM.EdgeWeight[k][disMin[1][k]]; 137 k=disMin[1][k]; 138 } 139 path.add(GM.Vertex[k]); 140 } 141 char[] p=new char[path.size()]; 142 for(int i=0;i<p.length;i++){ 143 p[i]=path.get(i); 144 } 145 return new char[][]{p,{(char)l}}; 146 } 147 148 }
Graph.java
1 package com.itheima.controller; 2 /** 3 * 新建Graph类,用于存储数据 4 * @author Misui_user 5 * 6 */ 7 class GraphMatrix 8 { 9 public static final int MaxValue=65535; //最大值(可设为一个最大整数) 10 char[] Vertex; //保存顶点信息(序号或字母) 11 int GType=0; //图的类型(0:无向图,1:有向图) 12 int VertexNum; //顶点的数量 13 int EdgeNum; //边的数量 14 int[][] EdgeWeight; //保存边的权 15 /** 16 * 设置顶点 17 * @param points 18 */ 19 public void setVertex(char[] points){ 20 this.Vertex=new char[points.length]; 21 this.VertexNum=points.length; 22 for(int i=0;i<this.VertexNum;i++) //输入顶点 23 { 24 this.Vertex[i]=points[i]; //保存到各顶点数组元素中 25 } 26 } 27 /** 28 * 设置边及其权重 29 * @param roads 30 * @param weights 31 */ 32 public void setEdgeWeight(char[][] roads,int[] weights){ 33 this.EdgeWeight=new int[roads.length][roads.length]; 34 ClearGraph(); 35 this.EdgeNum=roads.length; 36 for(int k=0;k<this.EdgeNum;k++) //输入边的信息 37 { 38 int i=indexOf(roads[k][0]); //在已有顶点中查找始点位置 39 int j=indexOf(roads[k][1]); //在已有顶点中查找结终点 位置 40 this.EdgeWeight[i][j]=weights[k]; //对应位置保存权值,表示有一条边 41 if(this.GType==0) //若是无向图 42 { 43 this.EdgeWeight[j][i]=weights[k]; //在对角位置保存权值 44 } 45 } 46 } 47 /** 48 * 清空邻接矩阵 49 * @param GM 50 */ 51 private void ClearGraph() 52 { 53 for(int i=0;i<this.VertexNum;i++) //清空矩阵 54 { 55 for(int j=0;j<this.VertexNum;j++) 56 { 57 this.EdgeWeight[i][j]=MaxValue; //设置矩阵中各元素的值为MaxValue 58 } 59 } 60 } 61 public int indexOf(char c){ 62 for(int i=0;i<VertexNum;i++){ 63 if(c==Vertex[i]){ 64 return i; 65 } 66 } 67 return -1; 68 } 69 }
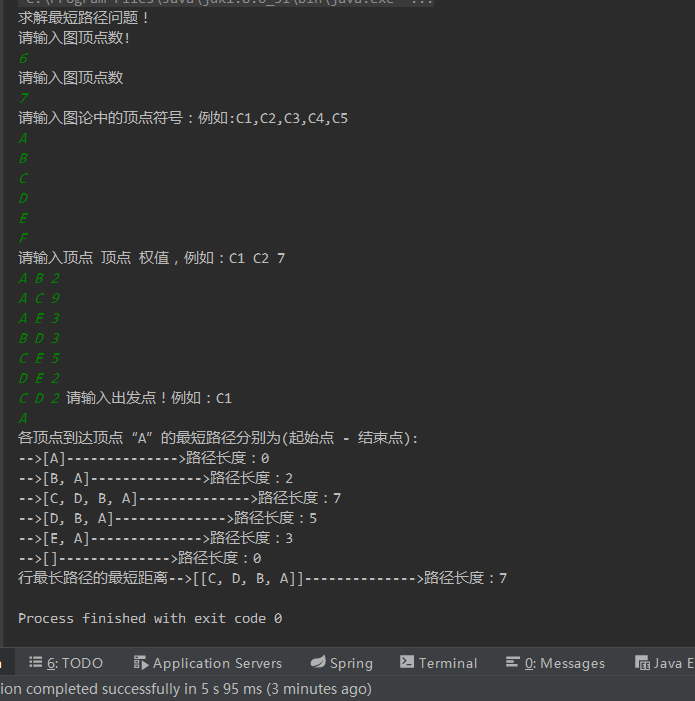
运行结果说明: