Hard | LeetCode 212. 单词搜索 II | 回溯 + 前缀树

212. 单词搜索 II

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：

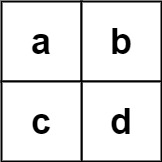
输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] 是一个小写英文字母
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] 由小写英文字母组成
• words 中的所有字符串互不相同

解题思路

方法一：回溯 + 前缀树优化

这道题和常见的DFS搜索题目类似。

比如 Medium | LeetCode 200. 岛屿数量 | 矩阵 + DFS 这道题DFS的条件是, 下一个节点必须是1(陆地)
比如 Hard | LeetCode 329. 矩阵中的最长递增路径 | 矩阵+DFS , 这道题DFS的条件是, 下一个节点值必须大于当前节点值

而在本题当中, DFS的条件是 当前节点在某个单词的路径上。

解决这个的思路可以是把从DFS起点到当前的所有字符取出来, 然后判断是否是单词列表的某个单词的前缀。这种方法可行, 但是复杂度很高。

有一种优化的方法：前缀树 (Medium | LeetCode 208. 实现 Trie (前缀树) | 设计)

在DFS的过程当中, 让矩阵当前位置 和 前缀树的节点 对应起来, 就很容易知道 下一个节点是否在某个单词的路径上。当DFS到矩阵的某个位置, 其对应的在前缀树的节点 是代表一个单词的时候, 就将其加入到结果集当中。

同时在将某个单词添加进结果集的时候, 可以将前缀树的word标志置为null, 因为这个单词已经加进去了, 不会再添加了。
如果这个被添加进结果集的单词的节点是叶节点的时候, 可以删除这个单词的路径上的节点。这样可以提高效率。

代码

前缀树的数据结构编码

static class TrieTree {

    static class TrieNode {
        // 用来保存当前节点的所有孩子节点的字符以及节点映射信息
        private HashMap<Character, TrieNode> children = new HashMap<>();
        // 用来表示当前节点是否代表一个单词
        private String word;

        public void setWord(String word) {
            this.word = word;
        }

        private boolean containCharChild(Character c) {
            return children.containsKey(c);
        }

        private TrieNode getCharChild(Character c) {
            return children.get(c);
        }

        private TrieNode addCharChild(Character c) {
            TrieNode rtn  = new TrieNode();
            children.put(c, rtn);
            return rtn;
        }
    }

    private TrieNode root;

    public TrieTree() {
        this.root = new TrieNode();
    }

    public TrieNode getRoot() {
        return root;
    }

    public void addWord(String word) {
        char[] wordArray = word.toCharArray();
        TrieNode cur = root;
        for (char c : wordArray) {
            if (cur.containCharChild(c)) {
                cur = cur.getCharChild(c);
            } else {
                cur = cur.addCharChild(c);
            }
        }
        cur.setWord(word);
    }

    public void removeWord(String word) {

    }

    public void show() {
        dfsShowCore(root);
    }

    private void dfsShowCore(TrieNode parents) {
        if (parents.children.isEmpty()) {
            System.out.println();
        }
        for (Entry<Character, TrieNode> trieNodeEntry : parents.children.entrySet()) {
            TrieNode node = trieNodeEntry.getValue();
            System.out.print(trieNodeEntry.getKey());
            if (node.word != null) {
                System.out.print(String.format(" (%s)", node.word));
            }
            if (!node.children.isEmpty()) {
                System.out.print(" -> ");
            }
            dfsShowCore(node);
        }
    }
}

代码主体部分

public List<String> findWords(char[][] board, String[] words) {
    // 先根据单词列表构造前缀树
    TrieTree trie = new TrieTree();
    for (String word : words) {
        trie.addWord(word);
    }
    trie.show();
    TrieNode root = trie.getRoot();
    List<String> res = new ArrayList<>();
    for (int row = 0; row < board.length; ++row) {
        for (int col = 0; col < board[row].length; ++col) {
            if (root.containCharChild(board[row][col])) {
                backtracking(board, row, col, root, res);
            }
        }
    }
    return res;
}

private void backtracking(char[][] board, int row, int col, TrieNode parent, List<String> res) {
    Character letter = board[row][col];
    TrieNode curNode = parent.getCharChild(letter);

    // 找到一个单词
    if (curNode.word != null) {
        res.add(curNode.word);
        // 这个单词已经加进结果集了, 不会添加重复的单词, 所以将当前节点代表的单词删除
        curNode.word = null;
    }

    // 保证每一次枚举过程, 这个位置的字符不会重复使用, 使用"#"号标记, 这轮枚举结束之后回溯时, 会将其还原。
    board[row][col] = '#';

    // DFS遍历其他相邻的位置
    int[] rowOffset = {-1, 0, 1, 0};
    int[] colOffset = {0, 1, 0, -1};
    for (int i = 0; i < 4; ++i) {
        int newRow = row + rowOffset[i];
        int newCol = col + colOffset[i];
        if (newRow < 0 || newRow >= board.length || newCol < 0
                || newCol >= board[0].length) {
            continue;
        }
        if (curNode.containCharChild(board[newRow][newCol])) {
            backtracking(board, newRow, newCol, curNode, res);
        }
    }

    // 还原初始字母
    board[row][col] = letter;

    // 对于 Trie 中的叶节点，一旦遍历它（即找到匹配的单词），就不需要再遍历它了, 所以可以直接删除
    // 如果删除某个不是单词的叶节点, 那么遍历到这个叶节点也没有意义了, 同样删除掉。
    if (curNode.children.isEmpty()) {
        parent.children.remove(letter);
    }
}