排序算法系列1--简单排序（选择，冒泡，直接插入，希尔排序）

排序是数据处理中十分常见的操作，现代高级语言都有现成的n种排序算法。但了解它们的代码，对计算机思维有帮助。

 

简单选择排序

每一趟从待排序的数据元素中选择最小（或最大）的一个元素作为首元素，直到所有元素排完为止，简单选择排序是不稳定排序。

无论数组原始排列如何，比较次数都不变；变的是交换次数。完全有序的情况下无需交换移动元素，最差情况下（把数组倒序改成正序），交换次数最多: n-1。

时间复杂度是n²

 

冒泡排序 

以前的博文：https://www.cnblogs.com/chentianwei/p/8244728.html

比较相邻的两个元素，如果他们的顺序错误就把他们交换过来。

n个数，进行n-1轮比较。 每轮归位1个最大／最小数，已经归位的数下一轮无需再比较。

冒泡的比喻就是：每轮把最大/最小值放到数组的最后。好像冒气泡。

时间复杂度是n²

 

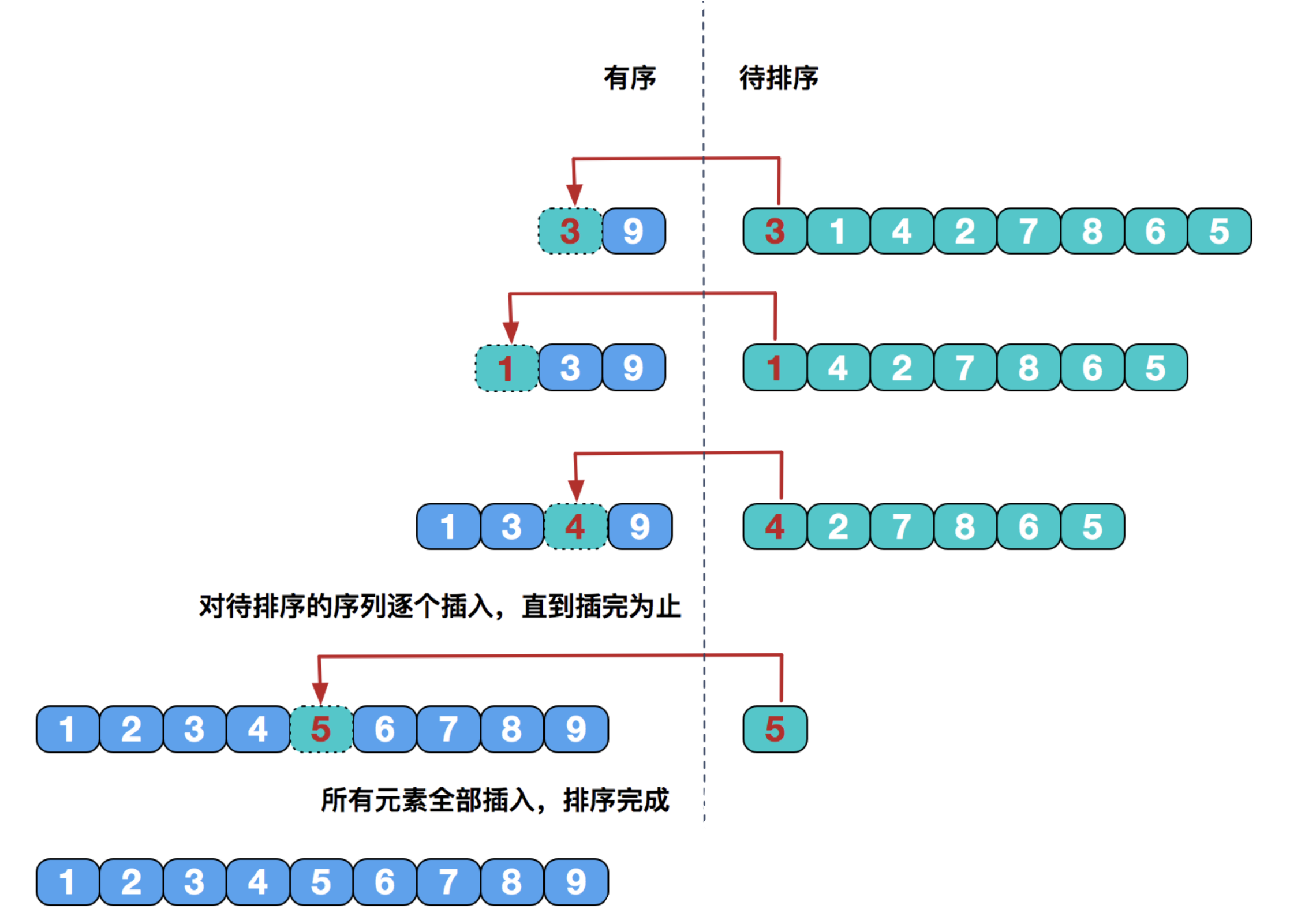
直接插入排序

直接插入排序基本思想是每一步将一个待排序的记录，插入到前面已经排好序的有序序列中去，直到插完所有元素为止。

简单插入排序在最好情况下，需要比较n-1次，无需交换元素，时间复杂度为O(n);在最坏情况下，时间复杂度依然为O(n²)。但是在数组元素随机排列的情况下，插入排序还是要优于上面两种排序的。

时间复杂度依然为n²

 

---

希尔排序 

git代码

也称为：in-place comparison sort。

⚠️in place algorithm即原地算法：基本不需要额外辅助的数据结构，可能需要少量额外的辅助变量来转换数据的算法。

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。 

⚠️递减增量： 每轮逐步减少步长。步长是“将要比较的2个元素”中间间隔的其他元素的数量。

算法的实现：

这个算法是计算机早期的一种算法，比冒泡，插入速度更快。这是因为这个算法的元素比较，不是相邻的连个元素比较，而是一个元素和距离它较远的元素进行比较。即用较大的步子长度来降低比较的次数，这样速度就快了很多。

举例：

数组a, 有12个元素。使用步长5，3，1。如图。

 

  

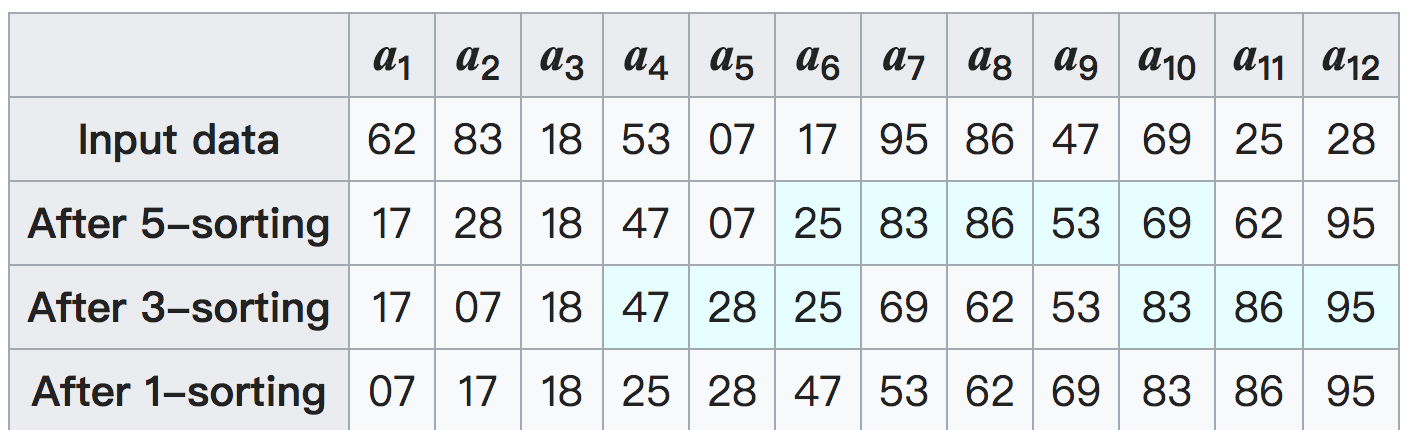
第一次以步长等于5分组。结果可见：

17， 28，18，47，  07

25，83，86，53， 69

62，95

第一列到第5列都是从小到大的正序排列了。

理论的sort方式：

1. 按照元素之间的gap分组。“对分组的元素进行排序”。（在数组原位置进行比较和交换，即in-place）。
2. ⚠️，关于第一步的具体方法见代码说明。
3. 减少元素之间的gap。这样分到一组的元素增加了。还是按照第一步操作。
4. 递减gap操作，即每次都减少元素之间的gap，直到没有距离, 即所有的元素都分在一组。排序后，就是一个有序数组。

关于第二步骤：

每组元素都需要进行排序操作，如何做到？ 使用插入排序法：

首先, 对分到同组元素，前两个元素比较和交换，成为有序数组。

然后，第3个元素和第2，1个元素比较并插入到合适的位置。

再后，如同上一步，第4个元素，和第3，2，1个元素比较并插入。

最后，当最后一个元素被插入到合适位置后，本组元素排序完成。

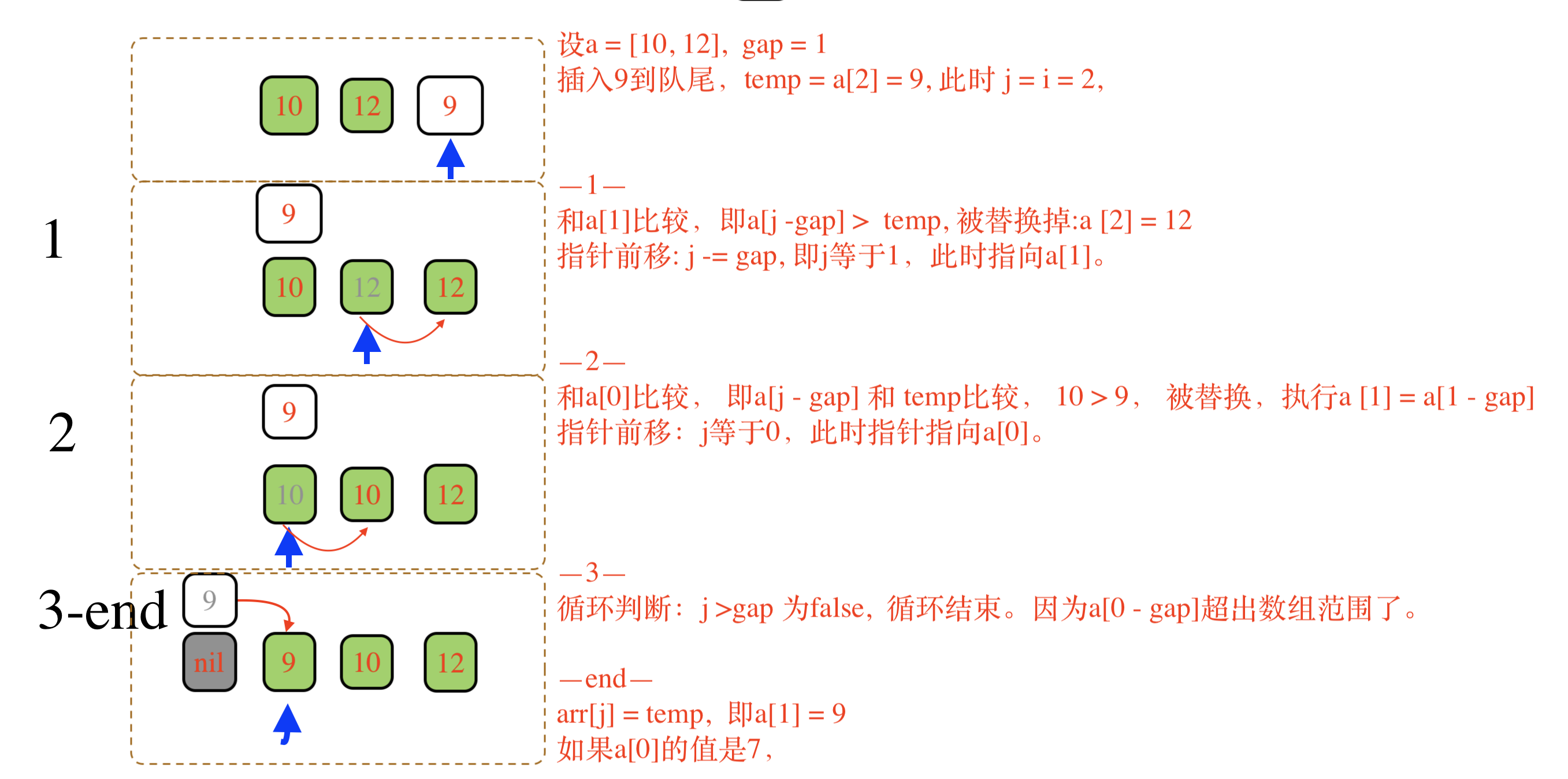
因为原数组a是无序的，并使用gap_sort。所以当gap = 3则，设置i =3。

要比较数组的所有元素，所以遍历从i到length -1的所有元素，每个元素都用插入排序法。因为0到i-1的元素和i到i +gap比较，所以无需遍历：

    i = gap
    while i < arr.length
      temp = arr[i]
      # 插入排序
      #...
      i += 1
    end

深入i循环内部，每个i的插入排序：

    while i < arr.length
      temp = arr[i]
      j = i
      while j >= gap && arr[j - gap] > temp
        arr[j] = arr[j-gap]
        j -= gap
      end
      arr[j] = temp
      i += 1
    end

arr[j]和它同组的前面的元素arr[j - gap], 比较大小。

变量j的第1..(1+ gap)次循环内部：每次只有2个元素比较，相当于第2个元素插入到第1个元素的前面或后面。形成只有2个元素的有序数列。

上面的插入代码不太好理解, 其实就是插入排序法。

可以这么想或理解：

• 把gap假设是数字1，即同组元素相邻
• 把待插元素放到数组尾部，从尾部往头部的方向，逐个和待插值比较。

具体代码见下面。

总结：

步长的选择是希尔排序的最关键的部分。

算法开始以一定的步长进行排序。然后会逐步减少步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为普通插入排序。

Donald Shell最初建议步长选择n/2，然后每轮对上轮的步长取半, 直到步长达到1。即{n/2,(n/2)/2...1}。

步长的选择，和数列的特性（大数据，带小数等）决定了整体的时间复杂度。所以这个排序法是不稳定的。

当步长是n/2ⁱ，最坏情况下仍然是O(n²)。

Ruby代码：（使用步长 n/2ⁱ），便于理解的代码：

def shell_sort(arr)
  gap = arr.length/2
  # 使用的是n除以2的i次方的步距。最后一轮gap等于1.
  while gap > 0
    i = gap
    # 遍历从i开始的元素， i前面的元素无需遍历。因为插入排序法，从后往前比较。
    while i < arr.length
      # 设置指针j, 指针是要前移的。
      # 相当于在队尾插入一个新元素，然后和前面的同组相邻元素比较和交换位置。
      # 如此反复直到该元素找到确定位置。
      j = i
      while j >= gap && arr[j - gap] > arr[j]
        # 被分到同组的相邻元素交换位置
        temp = arr[j]
        arr[j] = arr[j - gap]
        arr[j - gap ] = temp
        # 指针前移一个位置
        # 此时，arr[j]位置的值是插入的元素，它会在下轮循环和前面的元素比较。
        j = j - gap
      end
      i += 1
    end
    gap = gap/2
  end
  return arr
end

p b = (1..50).to_a.shuffle

p shell_sort(b)

上面对被分组的元素使用的排序法，不是插入排序，而是类似冒泡排序，即每次比较相邻两个元素并交换值value。

有更节省时间的改进代码：

无需每次都交换值。把待插入元素和前面的同组元素一一比较，只移动大于该元素的元素的value，最后再插入这个元素的value即可。这样节省了很多时间。

def shell_sort(arr)
  gap = arr.length / 2

  while gap > 0
    i = gap
    # 遍历从i开始的元素， i前面的元素无需遍历。因为插入排序法，从后往前。
    while i <= arr.length - 1
      temp = arr[i]
      j = i
      while j >= gap && arr[j - gap] > temp
        arr[j] = arr[j - gap]
        # arr[j - gap] = temp
        j = j - gap
      end
      # 最后插入值。
      arr[j] = temp
      i += 1
    end
    gap = gap/2
  end
  return arr
end

p b = (1..12).to_a.shuffle
p shell_sort(b)

https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F 

参考：https://www.cnblogs.com/chengxiao/p/6103002.html