1.学习总结(2分)
1.1树结构思维导图

1.2 树结构学习体会
建树可以用递归或者利用队列,其中我认为较难的是递归,容易让我的思路混淆,还需多加练习。
2.PTA实验作业(4分)
2.1 题目1:6-4 jmu-ds-表达式树
2.2 设计思路(伪代码或流程图)
(计算表达式树)
建立存储树的栈 b
存储字符的栈 c
若输入的字符为数字,则建立存储该数字的树且存入栈b
若输入的字符为运算符
若输入的字符优先级小于等于栈c的字符
则取出栈b中的两个树
以及栈c中的字符,构造以栈c字符为父节点,栈b树为左右节点的树,并将该数存入栈b
若优先级相等
则表示右括号遇到左括号,将左括号取出,continue
存入该运算符
while (!c.empty)
则取出栈b中的两个树
以及栈c中的字符,构造以栈c字符为父节点,栈b树为左右节点的树,并将该数存入栈b
(建表达式的二叉树)
若该节点为运算符
return 左孩子与右孩子与该运算符对应的运算
若该运算符为 ‘/’,则判断右结点是否为0
若该节点不为运算符
return T -> data - '0'
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

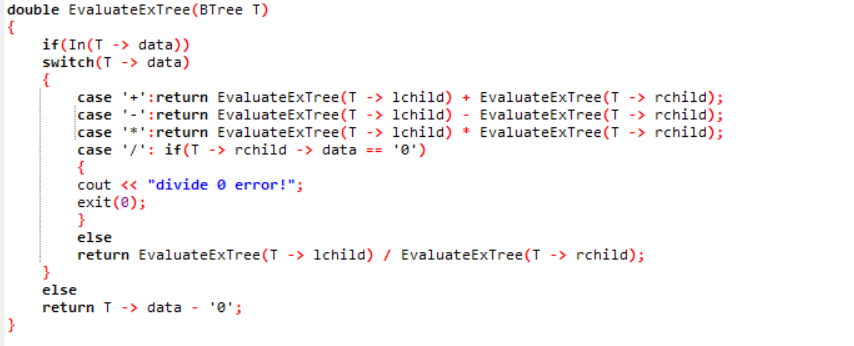
2.4 PTA提交列表说明。

多种错误是因为遇到括号时取出了2次符号,而我已经用了continue跳过右括号入栈的步骤,因此只需去出一次括号,如下图

2.5 题目1:7-1 还原二叉树
2.6 设计思路(伪代码或流程图)
(还原二叉树函数)
btree rebuild(char f[],char m[],int min,int max),f为先序,m为中序,min和max为左右边界
起初max为结点数减一,min为0,全局变量fi = 0代表字符串f[fi](前序字符串)第一个字符
构建树结点 t
若min > max
表示该节点为空,返回NULL
for i=min to max
查找中序字符串中与先序字符串f[fi]相等的字符
并且fi ++,用于下一次查找
令该结点 t -> data = m[i]
t -> lchild = rebuild(f,m,min,i-1);
t -> rchild = rebuild(f,m,i+1,max);
返回t
(判断树的高度函数)
若b为空
返回 0
否则
令 a = GetHeight( BT -> lchild);
b = GetHeight( BT -> rchild);
返回 a +1 与 b + 1 中大的值
2.7 代码截图
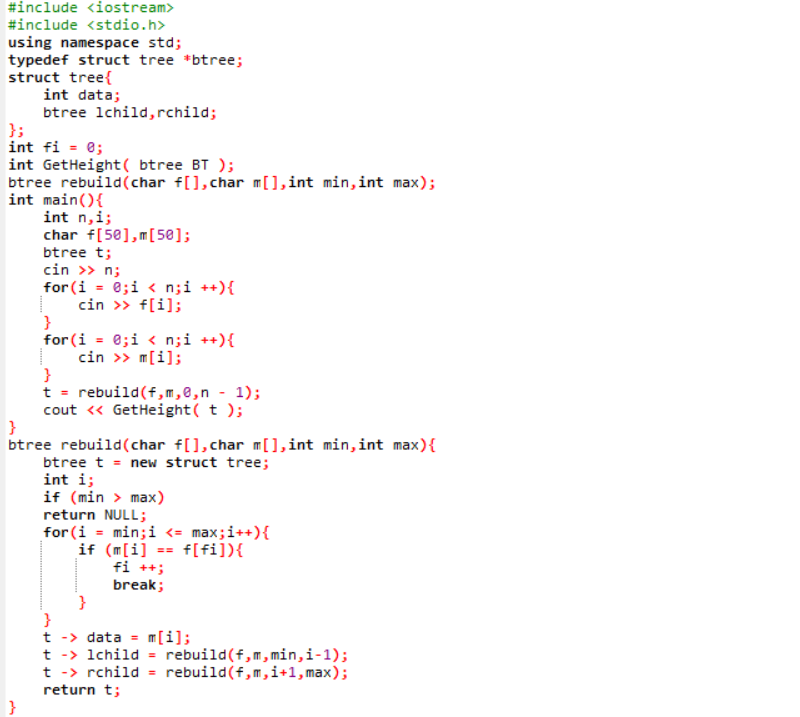
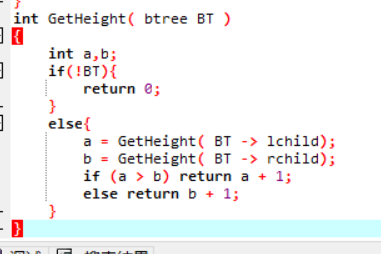
2.8 PTA提交列表说明。

无明显错误(编译错误是因为用错了编译器)
2.9 题目1:7-3 jmu-ds-二叉树层次遍历
2.10 设计思路(伪代码或流程图)
构建树结点 b
建立用于存储树的队列 q
输出第一个结点并将该节点存入队列q中
while(队列不为空时)
取出队列中的树
若左节点不为空
输出左节点并且将该节点存入队列q
若右节点不为空
输出右节点并且将该节点存入队列q
2.11 代码截图
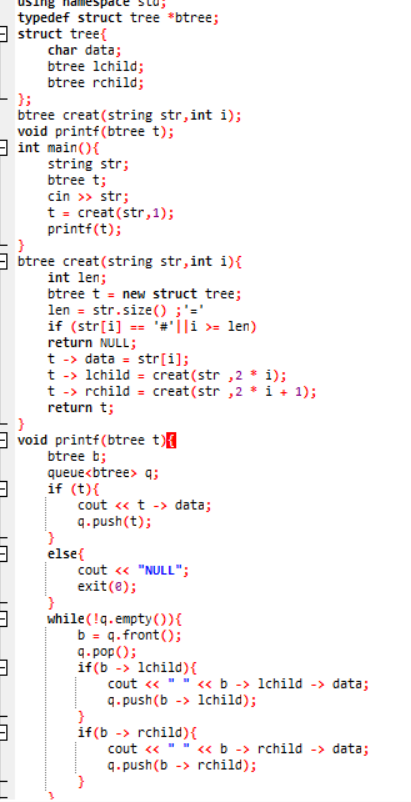
2.12 PTA提交列表说明。

建树时判断空结点的条件错误,缺少了 i <= len的条件导致部分错误
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名

3.2 我的得分:
180
4. 阅读代码(必做,1分)
#include<bits/stdc++.h>
using namespace std;
typedef struct BinTree Node;
typedef Node* BTree;
struct BinTree{
BTree left;
BTree right;
char data;
};
BTree findTree( char*in , char*pre , int n )
{
if( n<=0 )
return NULL;
BTree t = new Node;
t->data = *pre;
int i;
for( i=0 ; i<n ; i++ )
if( in[i] == *pre )
break;
t->left = findTree( in , pre+1 , i);
t->right = findTree( in+i+1 , pre+i+1 , n-i-1 );
return t;
}
int Getlen( BTree t ) {
if( !t )
return 0;
return max( Getlen(t->left),Getlen(t->right) ) + 1;
}
int main() {
char pre[55] , in[55];
int n;
cin >> n;
cin >> pre;
cin >> in;
BTree bt = new Node;
bt = findTree( in , pre , n );
cout << Getlen( bt ) << endl;
}
吴某的还原二叉树代码,他的还原二叉树函数用了一个变量n,而我用了2个变量 max 和 min来判断是否为空结点,相比之下,他的方法更简洁。
5. 代码Git提交记录截图