【CF1007D】Ants（树链剖分+2-SAT）

题目链接

• 有一棵 (n) 个点的树。
• 你需要进行 (m) 次染色操作，每次操作给定两个点对 ((x_1,y_1)) 和 ((x_2,y_2))，你需要选择一个点对将对应树上路径中的边全部染上颜色。要求同一条边不能被重复染色。
• 求一种合法方案。
• (2le nle10^5)，(1le mle10^4)

2-SAT

每种染色操作需要在两个点对中选出恰好一个，显然是经典的 2-SAT 问题。

建图就是考虑两个路径存在交集的点对不能同时选择。

树链剖分优化建图

把每条边记在两个端点中深度较大的那个上。

对于每个点对 ((x,y)) 需要给它的路径上的所有边打标记，就相当于给除 (operatorname{LCA}(x,y)) 以外 (x,y) 路径上的所有点打标记。

打标记的过程可以用树链剖分+线段树优化实现。

然后对于线段树上存在祖先-后代关系的节点上的标记（包括同一节点上），它们不能同时选择。

如果仅仅是同一节点上的标记不能同时选择，有一种经典的前缀优化建图：（要从所有的 (1) 向除自己对应点外的所有的 (0) 连边，(A,B) 为辅助点）

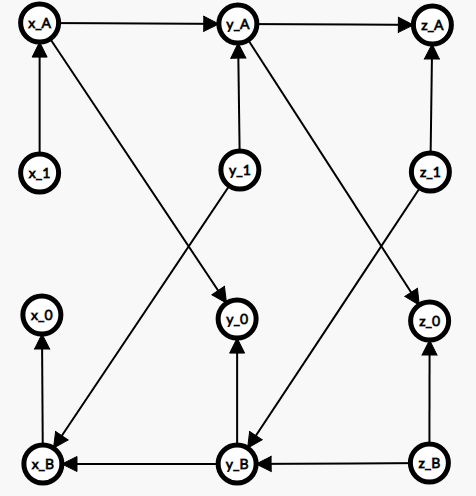
而要让存在祖先-后代关系的节点上的标记都不能同时选择，由于前缀优化建图的过程中我们只需要知道最后一次建图增加的两个辅助点，那么其实可以让两个子节点都在 从线段树根节点到当前点为止，前缀优化建图的最后两个辅助点 的基础上继续建图。容易发现它们的连边是互不干扰的。

代码：(O(nlog^2n))

#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Rg register
#define RI Rg int
#define Cn const
#define CI Cn int&
#define I inline
#define W while
#define N 100000
#define M 10000
#define add(x,y) (e[++ee].nxt=lnk[x],e[lnk[x]=ee].to=y)
using namespace std;
int n,m,ee,lnk[N+5];struct edge {int to,nxt;}e[N<<1];
namespace FastIO
{
	#define FS 100000
	#define tc() (FA==FB&&(FB=(FA=FI)+fread(FI,1,FS,stdin),FA==FB)?EOF:*FA++)
	#define pc(c) (FC==FE&&(clear(),0),*FC++=c)
	int OT;char oc,FI[FS],FO[FS],OS[FS],*FA=FI,*FB=FI,*FC=FO,*FE=FO+FS;
	I void clear() {fwrite(FO,1,FC-FO,stdout),FC=FO;}
	Tp I void read(Ty& x) {x=0;W(!isdigit(oc=tc()));W(x=(x<<3)+(x<<1)+(oc&15),isdigit(oc=tc()));}
	Ts I void read(Ty& x,Ar&... y) {read(x),read(y...);}
	Tp I void writeln(Ty x) {W(OS[++OT]=x%10+48,x/=10);W(OT) pc(OS[OT--]);pc('
');}
}using namespace FastIO;
namespace G
{
	#define PS M*1200
	#define ES M*1800
	int ee,lnk[PS+5];edge e[ES+5];I void Add(CI x,CI y) {add(x,y);}
	int d,dfn[PS+5],low[PS+5],T,S[PS+5],IS[PS+5],ct,bl[PS+5];I void dfs(CI x)//Tarjan
	{
		dfn[x]=low[x]=++d,IS[S[++T]=x]=1;for(RI i=lnk[x],y;i;i=e[i].nxt)
			dfn[y=e[i].to]?IS[y]&&(low[x]=min(low[x],dfn[y])):(dfs(y),low[x]=min(low[x],low[y]));
		if(dfn[x]==low[x]) {++ct;W(bl[S[T]]=ct,IS[S[T]]=0,S[T--]^x);}
	}
	I void Solve()
	{
		RI i;for(i=1;i<=2*m;++i) !dfn[i]&&(dfs(i),0);
		for(i=1;i<=m;++i) if(bl[i]==bl[i+m]) return (void)puts("NO");puts("YES");//无解
		for(i=1;i<=m;++i) puts(bl[i]<bl[i+m]?"1":"2");
	}
}
namespace T
{
	int d,D[N+5],dfn[N+5],sz[N+5],f[N+5],g[N+5],tp[N+5];
	int ct;I void U(int& k,CI x)//在辅助点k-1,k的基础上前缀优化建图
	{
		RI y=x<=m?x+m:x-m,o=2*m+(ct+=2);G::Add(x,o-1),G::Add(o,y);
		if(k) G::Add(k-1,o-1),G::Add(k-1,y),G::Add(x,k),G::Add(o,k);k=o;
	}
	class SegmentTree
	{
		private:
			#define PT CI l=1,CI r=n,CI rt=1
			#define LT l,mid,rt<<1
			#define RT mid+1,r,rt<<1|1
			vector<int> G[N<<2];
		public:
			I void A(CI L,CI R,CI id,PT)//区间打标记
			{
				if(L<=l&&r<=R) return (void)G[rt].push_back(id);RI mid=l+r>>1;L<=mid&&(A(L,R,id,LT),0),R>mid&&(A(L,R,id,RT),0);
			}
			I void Walk(RI k=0,PT)//优化建图
			{
				for(vector<int>::iterator it=G[rt].begin();it!=G[rt].end();++it) U(k,*it);//加上当前点的标记
				if(l==r) return;RI mid=l+r>>1;Walk(k,LT),Walk(k,RT);//两个子节点都在当前点最终辅助点的基础上继续建图
			}
	}S;
	I void dfs1(CI x)//树剖第一次dfs
	{
		sz[x]=1;for(RI i=lnk[x],y;i;i=e[i].nxt) (y=e[i].to)^f[x]&&(D[y]=D[f[y]=x]+1,dfs1(y),sz[x]+=sz[y],sz[y]>sz[g[x]]&&(g[x]=y));
	}
	I void dfs2(CI x,CI t)//树剖第二次dfs
	{
		if(dfn[x]=++d,tp[x]=t,g[x]) {dfs2(g[x],t);for(RI i=lnk[x],y;i;i=e[i].nxt) (y=e[i].to)^f[x]&&y^g[x]&&(dfs2(y,y),0);}
	}
	I void A(RI x,RI y,CI id)//树剖给树上路径（除LCA）打标记
	{
		W(tp[x]^tp[y]) D[tp[x]]<D[tp[y]]&&(swap(x,y),0),S.A(dfn[tp[x]],dfn[x],id),x=f[tp[x]];D[x]>D[y]&&(swap(x,y),0),x^y&&(S.A(dfn[x]+1,dfn[y],id),0);
	}
}
int main()
{
	RI i,x,y;for(read(n),i=1;i^n;++i) read(x,y),add(x,y),add(y,x);T::dfs1(1),T::dfs2(1,1);
	RI a,b,c,d;for(read(m),i=1;i<=m;++i) read(a,b,c,d),T::A(a,b,i),T::A(c,d,i+m);return T::S.Walk(),G::Solve(),0;
}