一、
简介:现实生活中,我们最常见的数为十进制数,比如交通信号灯上的数字,电子表上的时间等。
相关换算
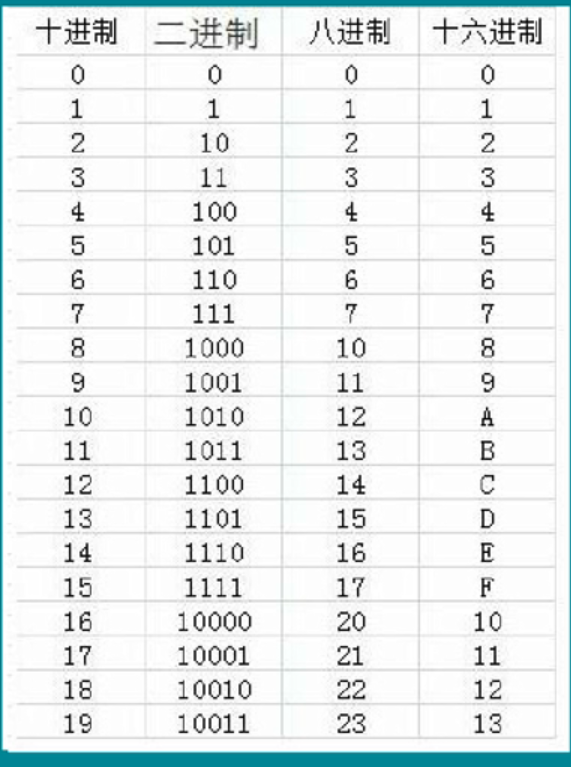
2进制,用两个阿拉伯数字:0、1;
8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;
10进制,用十个阿拉伯数字:0到9;
16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?
用竖式计算:
2AF5换算成10进制:
第0位: 5 * 16^0 = 5
第1位: F * 16^1 = 240
第2位: A * 16^2 = 2560
第3位: 2 * 16^3 = 8192 +
-------------------------------------
10997
直接计算就是:
5 * 16^0 + F * 16^1 + A * 16^2+2 * 16^3 = 10997 [1]
(别忘了,在上面的计算中,A表示10,而F表示15)
二进制数在C#中的写法:
byte b=0b01111110
二进制字符串的解释:
string bstr="0111110"; byte b=Convert.ToByte(bstr,2) //b=126
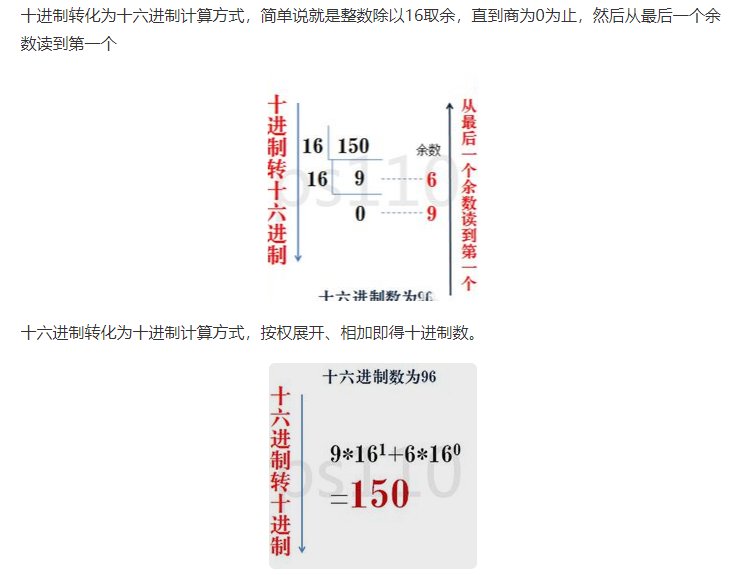
16转10
2转16
十进制转二进制
2进制转10进制

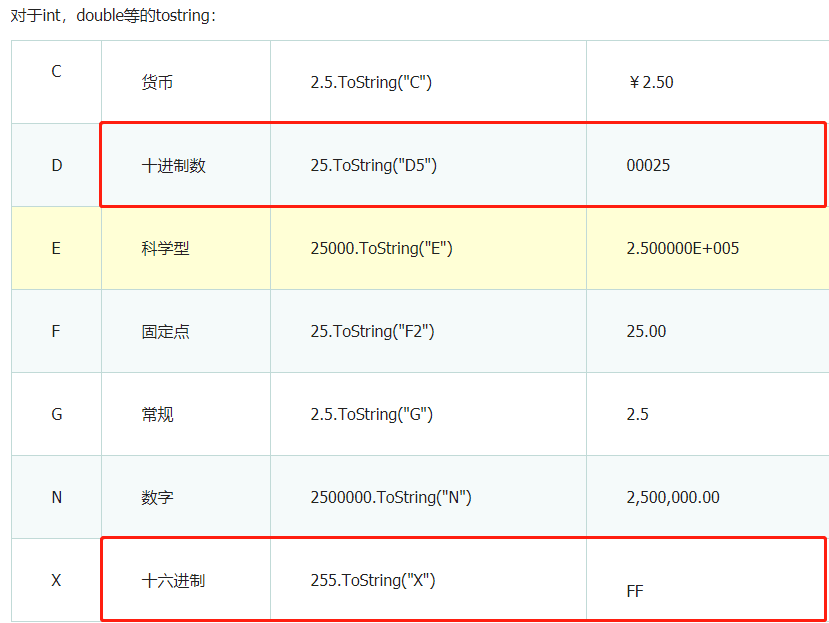
C# ToString("x2")的理解
1).转化为16进制。
2).大写X:ToString("X2")即转化为大写的16进制。
3).小写x:ToString("x2")即转化为小写的16进制。
4).2表示输出两位,不足的2位的前面补0,如 0x0A 如果没有2,就只会输出0xA
二、使用C#语句转换
二进制在C#中无法直接表示,我们一般用0和1的字符串来表示一个数的二进制形式。比如4的二进制为“100”。下面介绍C#里面用于进制转换的方法。
十进制转换为二进制(int-->string)
System.Convert.ToString(d, 2);// d为int类型 以4为例,输出为100
十六进制转换为二进制(int-->string)
System.Convert.ToString(d, 2);// d为int类型 以0X14为例,输出为10100
上面ToString函数的第二个参数表示目标数字系统的基数。
二进制转换为十进制(string-->int)
System.Convert.ToInt32(s, 2);// d为string类型 以“1010”为例,输出为10
十六进制转换为十进制(string-->int、int-->int)
方法一:
System.Convert.ToString(0xa,10);// 以0XA为例,输出为10
或者
System.Convert.ToInt32("0x41", 16);//以"0x41"为例,输出为65
方法二:
System.Int32.Parse(s, System.Globalization.NumberStyles.HexNumber);//s为string类型,以“41”为例,输出为65
注意这里的s中不能带有“0X”或者“0x”,区别于上面的方法。
二进制转换为十六进制(string-->int)
先转换为十进制,在转换为十六进制
string.Format("{0:X}",System.Convert.ToInt32(s, 2));// s为string类型 以“1010”为例,输出为A
十进制转换为十六进制
十进制转换为十六进制不需要特殊的方法,只要对输出格式进行控制一下就可以。
或者使用string.Format("{0:x}", dec)方法进行控制,也可以用s.ToString("X")方式进行控制。
除了数制转换之外,数据类型的转换也比较重要。对于基本数据类型,byte、char、int、string以及它们的数组形式的转换虽然简单,但是比较基础的知识。网上也有很多详解,用到的时候自行查阅即可。
三、位运算符
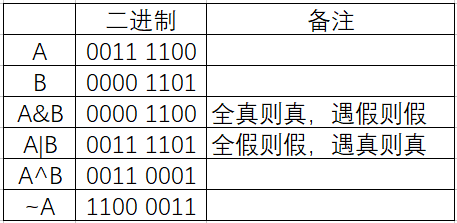
位运算符作用于位,并逐位执行操作。&、 | 和 ^ 的真值表如下所示:
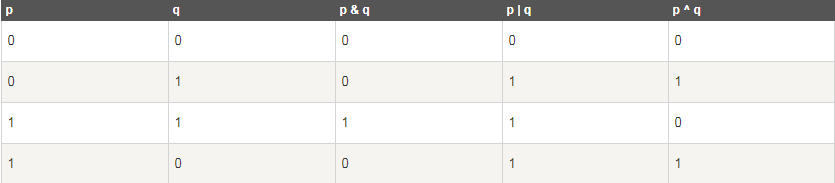
假设如果 A = 60,且 B = 13,现在以二进制格式表示,它们如下所示:
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011
下表列出了 C# 支持的位运算符。假设变量 A 的值为 60,变量 B 的值为 13,则:

代码:

using System;
namespace OperatorsAppl
{
class Program
{
static void Main(string[] args)
{
int a = 60; /* 60 = 0011 1100 */
int b = 13; /* 13 = 0000 1101 */
int c = 0;
c = a & b; /* 12 = 0000 1100 */
Console.WriteLine("Line 1 - c 的值是 {0}", c );
c = a | b; /* 61 = 0011 1101 */
Console.WriteLine("Line 2 - c 的值是 {0}", c);
c = a ^ b; /* 49 = 0011 0001 */
Console.WriteLine("Line 3 - c 的值是 {0}", c);
c = ~a; /*-61 = 1100 0011 */
Console.WriteLine("Line 4 - c 的值是 {0}", c);
c = a << 2; /* 240 = 1111 0000 */
Console.WriteLine("Line 5 - c 的值是 {0}", c);
c = a >> 2; /* 15 = 0000 1111 */
Console.WriteLine("Line 6 - c 的值是 {0}", c);
Console.ReadLine();
}
}
}
结果:

左移右移

转载:
1、https://www.cnblogs.com/hitfredrick/p/6403003.html
2、https://www.runoob.com/csharp/csharp-operators.html
3、https://blog.csdn.net/qq_38158479/article/details/103151281

