问题越学越多...
二分图简介
二分图又称作二部图,是图论中的一种特殊模型。
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
也就是说,只要两个点之间有边,那么这两个点就不能同属一个集合,必须分在两边。(就是不能相处的人连一条边
(并不是所有的无向图G都能转化为二分图。
定理:无向图G为二分图的充要条件是,该图至少有两个顶点,且其所有回路(环)的长度均为偶数。|就是随便找个环,长度都是偶数
二分图染色|判定
模板
https://codeforces.ml/problemset/problem/687/A
题目大意:有n个点,m条边,求是否能将所有的点分成两组,其中与每条边相连的两个点位于不同组。孤立的点不用管。如果不能输出-1.
#include<bits/stdc++.h> using namespace std; const int N=1e5+5; int n,m,x,y,use[N]; vector < int > f[N]; set <int> s1,s2; void dfs(int x,int col) { if(use[x]==0) use[x]=col; else { if(use[x]!=col) { printf("-1 "); exit(0); } if(use[x]==col) return ; } for(auto i:f[x]) dfs(i,col%2+1); } int main() { scanf("%d %d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d %d",&x,&y); f[x].emplace_back(y); f[y].emplace_back(x); } for(int i=1;i<=n;i++) { if(!f[i].size()||use[i]!=0) continue; dfs(i,1); } for(int i=1;i<=n;i++) { if(use[i]==1) s1.insert(i); if(use[i]==2) s2.insert(i); } printf("%d ",int(s1.size())); for(auto i:s1) printf("%d ",i); printf(" %d ",int(s2.size())); for(auto i:s2) printf("%d ",i); return 0; }
二分图最大匹配:
定义:在一个无向图中,定义一条边覆盖的点为这条边的两个端点。
找到一个边集S包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。
匈牙利算法:
建立有向图G,分为二分图的左侧和右侧。 优先选择左侧序号更小的连接可能的边。 对于两个点的目标点“冲突”的时候,采取“协商”的办法。 即序号小的连接可能连接的另一条边。 若“协商”失败,则放弃序号较大的点的边。
概念看的都好绕,实例比较好懂:
转自https://blog.csdn.net/qq_41730082/article/details/81162561
你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
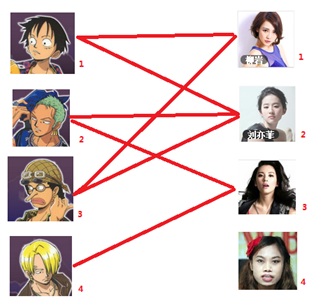
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
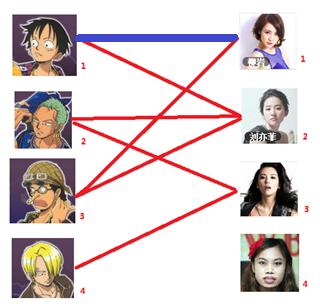
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
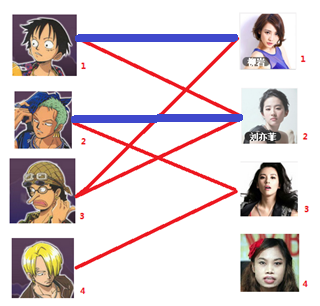
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
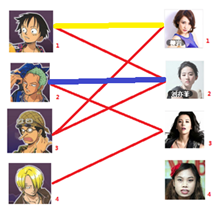
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
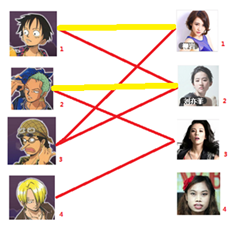
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
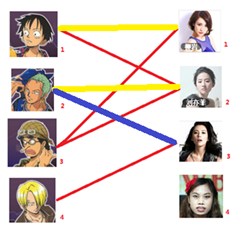
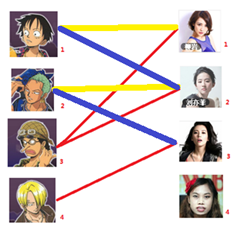
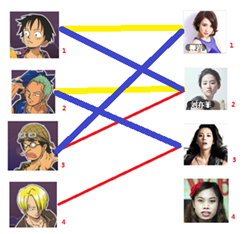
所以第三步最后的结果就是:
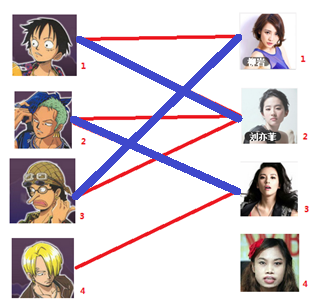
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
 图源来自https://www.cnblogs.com/jianglangcaijin/p/6035945.html
图源来自https://www.cnblogs.com/jianglangcaijin/p/6035945.html
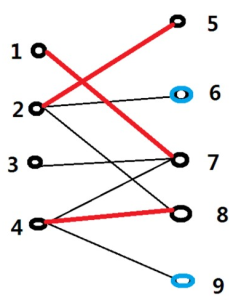
根据上面的图,可以有2种建图方法,然而每种方法的结果取决于你枚举的点集和单向边和双向边:
1:编号从1~9连的边为双向边,枚举点集是1~9则输出的是6,1~4输出3
2:编号从1~9连的边是单向边,(A={1,2,3,4},B={5,6,7,8,9})枚举点集1~9输出的是3,1~4仍然是3
算法主体都是一样,感觉是数据太水才得到一样的结果,因为后面做题连单向边全都出问题了
bool dfs(int x) { for(auto i:f[x]) { if(use[i]==0) { use[i]=1; if(match[i]==0||dfs(match[i])) //如果fx所连的节点i暂时没有cp||现在与i匹配的那个人的cp还可以更换,则把i匹配为x { match[i]=x; return 1;//可以被匹配 } } } return 0; }
总结
连双向边结果与枚举点集有关且点的编号不能重复,如果枚举的是全部点集则输出的是能被匹配到点的个数(2*S)对建图没多大要求最方便
这样就方便理解下面的概念了
先别忘了最大匹配的定义:
在一个无向图中,定义一条边覆盖的点为这条边的两个端点。找到一个边集S包含最多的点,即使这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。
二分图的最小顶点 覆盖
定义:假如选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖所有的边。
证我就不会了,结论就是大小刚好等于最大匹配的数值(取的点完全不一样好吧)
证明可以看(我觉得写的很清楚https://www.cnblogs.com/jianglangcaijin/p/6035945.html
无向图的最小 路径 覆盖
无向二分图的最小路径覆盖=顶点数-分匹配(因为无向图就是双向的一条边等于两次入图正向和反向,最后得到的匹配数多了一倍所以要除以2才是原本的匹配数)
二分图的最大独立集
定义:选出一些顶点使得这些顶点两两不相连,则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。
最大独立集=所有顶点数-最小顶点覆盖
二分图的最大团
(感觉不怎么用因为就和独立集相反嘛)
定义:就是选出一些顶点,这些顶点两两之间都有边。最大团就是使得选出的这个顶点集合最大。(与最大独立集相反)
最大团=补图的最大独立集
因为最大独立集是两两不相连,所以最大独立集的补图两两相连。
所以如果你一道题建图不同,最大团刚好会和独立集反过来
例题
https://vjudge.net/contest/70017#problem/B
这里就是如果你要选的集合中有某个数,那么就不能出现它(某个素数)倍的数。
因为是有a不能有b所以可以反向建图(a-b),最后就是求两两不相连的最大子集(最大独立集) (双向边枚举所有点)
记得清空match等数组
#include<bits/stdc++.h> using namespace std; const int N=4e5+5,M=5e5+5; int n,T,k,maxn,x,b[M],ans,ss[M],match[N]; bool use[N],vis[M]; vector <int> f[N]; map <int ,int> mp; bool dfs(int x) { for(auto i:f[x]) { if(use[i]==0) { use[i]=1; if(match[i]==0||dfs(match[i])) //如果fx所连的节点i暂时没有cp||现在与i匹配的那个人的cp还可以更换,则把i匹配为x { match[i]=x; return 1; } } } return 0; } void pd() { use[1]=1; for(int i=2;i<=M-3;i++) { if(use[i]==0) ss[++k]=i; for(int j=1;j<=k&&ss[j]*i<=M-3;j++) { use[ss[j]*i]=1; if(i%ss[j]==0) break; } } } int main() { freopen("data.in","r",stdin); freopen("data.out","w",stdout); pd(); scanf("%d",&T); for(int l=1;l<=T;l++) { mp.clear(); memset(match,0,sizeof(match)); memset(b,0,sizeof(b)); memset(use,0,sizeof(use)); maxn=-1; ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&x); maxn=max(maxn,x); b[x]=i; mp.insert(make_pair(x,i)); } for(auto i:mp) { for(int j=1;j<=k&&i.first*ss[j]<=maxn;j++) { int temp=i.first*ss[j]; if(b[temp]!=0) { f[i.second].emplace_back(mp[temp]); f[mp[temp]].emplace_back(i.second); } } } for(int i=1;i<=n;i++) { memset(use,0,sizeof(use)); if(dfs(i)) ans++; } printf("Case %d: %d ",l,n-ans/2); for(int i=1;i<=n;i++) f[i].clear(); } return 0; } /* 3 5 2 4 8 16 32 5 2 3 4 6 9 3 1 2 3 */
然而过不了,因为这题时间卡的紧(居然卡sqrt的复杂度)
再也不用匈牙利了
Hopcroft_Karp算法:
hk是预先找到多条路径最短的增广路,然后再用匈牙利算法就沿着bfs找的路径去找增广路。不知道理解的对不对
增广路:
举例来说,二分图G={A,B},增广路由集合A中一个点通向集合B中一个点,再由B中这个点通向A中一个点……交替进行)。
也就是说用Hopcroft_Karp算法,你必须要想办法将集合分成两个集合,而不是像匈牙利算法那样可以遍历所有的点,它只遍历A|B集合中的点
所以之前找的规律1:
1:编号从1~9连的边为双向边,枚举点集是1~9则输出的是2*S,1~4输出S
下面模板我都连的是双向边,因为连单向边不知道为什么答案会多一|少一 建图姿势不正确?
这是比较非主流的模板感觉:
因为它用一个数组dep换了dx,dy,match换了A_B,B_A...,还有一个常数 dis 不知到干嘛的,枚举只枚举A集合,所以输出S,这个枚举所有点集输出会出问题...
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int M=5e5+5,N=4e4+5,INF=0x3f3f3f3f; int match[N],ans,dep[N],a[N],T,b[M],maxn,ss[M],k,dis,n; int vis[N],use[M]; vector <int> f[N]; map <int,int> mp; set <int> s[3]; queue<int>q; bool searchP() { while(!q.empty()) q.pop(); memset(dep,0,sizeof(dep)); dis=INF; for(auto i:s[0]) if(match[i]==0) q.push(i); while(!q.empty()) { int x=q.front(); q.pop(); if(dep[x]>dis) break; for(auto i:f[x]) { if(!dep[i]) { dep[i]=dep[x]+1; if(match[i]==0) dis=dep[i]; else dep[match[i]]=dep[i]+1,q.push(match[i]); } } } return dis!=INF; } bool dfs(int x) { for(auto i:f[x]) { if(vis[i]==0&&dep[i]==dep[x]+1) { vis[i]=1; if(match[i]&&dep[i]==dis) continue; if(match[i]==0||dfs(match[i])) { match[x]=i; match[i]=x; return 1; } } } return 0; } void pd() { use[1]=1; for(int i=2;i<=M-3;i++) { if(use[i]==0) ss[++k]=i; for(int j=1;j<=k&&ss[j]*i<=M-3;j++) { use[ss[j]*i]=1; if(i%ss[j]==0) break; } } } int check(int x)//判断x是属于s[0]|s[1] { if(use[x]==0) return 1; int tot=0; for(int j=1;j<=k&&ss[j]<=x;j++) { while(x%ss[j]==0) { tot++; x/=ss[j]; } } tot%=2; return tot; } int main() { // freopen("data.in","r",stdin); // freopen("test.out","w",stdout); pd(); scanf("%d",&T); for(int l=1;l<=T;l++) { mp.clear(); s[0].clear(); s[1].clear(); memset(match,0,sizeof(match)); memset(b,0,sizeof(b)); memset(a,0,sizeof(a)); maxn=-1; ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); maxn=max(maxn,a[i]); b[a[i]]=i; } for(int i=1;i<=n;i++) { s[check(a[i])].insert(i); for(int j=1;j<=k&&a[i]*ss[j]<=maxn;j++) { int temp=a[i]*ss[j]; if(b[temp]!=0) { f[i].emplace_back(b[temp]); f[b[temp]].emplace_back(i); } } } int ans=0; while(searchP())//HK { memset(vis,0,sizeof(vis)); for(auto i:s[0]) if(!match[i]&&dfs(i)) ans++; } for(int i=1;i<=n;i++) f[i].clear(); printf("Case %d: %d ",l,n-ans); } }
这个是主流的 数组真的多:
它bfs&&while(search_p())里面枚举的是所有点,所以输出的是2*S。这个只枚举A集合输出会有问题...迷惑
#include<bits/stdc++.h> using namespace std; const int N=4e5+5,M=5e5+5,inf=0x3f3f3f3f; int n,T,k,maxn,x,ans,dis,a[N],b[M],ss[M],dx[M],dy[M],A_B[M],B_A[M]; bool use[N],vis[M]; vector <int> f[N]; set <int> s[3]; queue <int> q; bool dfs(int x) { for(auto i:f[x]) { /* 找寻所有深度右边是左边+1的点,这样就相当于找增广路,看看增广路能否增广 */ if(vis[i]==0&&dy[i]==dx[x]+1) { vis[i]=1; if(B_A[i]!=0&&dy[i]==dis)//已经被匹配了 continue; if(B_A[i]==0||dfs(B_A[i])) //如果fx所连的右节点i暂时没有匹配||现在与i匹配的那个人的cp还可以更换,则把i匹配为x { A_B[x]=i;// x -> i B_A[i]=x;// i -> x return 1; } } } return 0; } void pd() { use[1]=1; for(int i=2;i<=M-3;i++) { if(use[i]==0) ss[++k]=i; for(int j=1;j<=k&&ss[j]*i<=M-3;j++) { use[ss[j]*i]=1; if(i%ss[j]==0) break; } } } bool find_expath() { memset(dx,0,sizeof(dx)); memset(dy,0,sizeof(dy)); dis=inf; while(!q.empty()) q.pop(); for(int i=1; i<=n;i++) { if(A_B[i]==0)//将所有未匹配的A集合的点加入队列 q.push(i); } while(!q.empty()) { int temp=q.front(); q.pop(); if(dx[temp]>dis) break; for(auto i:f[temp]) { if(dy[i]==0)//没访问过 { dy[i]=dx[temp]+1; if(B_A[i]!=0) { dx[B_A[i]]=dy[i]+1; q.push(B_A[i]); } else dis=dy[i]; } } } return dis!=inf; } int check(int x) { if(use[x]==0) return 1; int tot=0; for(int j=1;j<=k&&ss[j]<=x;j++) { while(x%ss[j]==0) { tot++; x/=ss[j]; } } tot%=2; return tot; } int main() { freopen("data.in","r",stdin); freopen("test.out","w",stdout); pd(); scanf("%d",&T); for(int l=1;l<=T;l++) { s[0].clear(); s[1].clear(); memset(A_B,0,sizeof(A_B)); memset(B_A,0,sizeof(B_A)); memset(vis,0,sizeof(vis)); memset(b,0,sizeof(b)); memset(a,0,sizeof(a)); maxn=-1; ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); maxn=max(maxn,a[i]); b[a[i]]=i; } for(int i=1;i<=n;i++) { s[check(a[i])].insert(i); for(int j=1;j<=k&&a[i]*ss[j]<=maxn;j++) { int temp=a[i]*ss[j]; if(b[temp]!=0) { f[i].emplace_back(b[temp]); f[b[temp]].emplace_back(i); } } } while(find_expath()) { memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { if(A_B[i]==0&&dfs(i)) { ans++; } } } printf("Case %d: %d ",l,n-ans/2); for(int i=1;i<=n;i++) f[i].clear(); } return 0; } /* 3 5 2 4 8 16 32 5 2 3 4 6 9 3 1 2 3 */
学得我一脸懵,还是无脑套模板吧