f(t) = t的傅里叶系数

　　计算机网络课程讲到物理层，布置作业的第一题是求f(t)=t (0≤t≤1)的傅里叶系数。

　　我们知道任何一个周期函数都可以被傅里叶级数逼近。如果是实值函数，则可以用正弦分量，余弦分量，直流分量来近似。公式如下：$$f(x)=frac{a_0}{2}+sum_{n=1}^{infty}(a_n cosnx+b_n sinnx)$$

　　利用正余弦函数的正交性反变换可得到f(x)的系数。本题中认为函数周期是1，进行延拓可以看成是无数个f(t)沿着x轴平移。

　　简单计算得$a_0=1$, $a_n=0$, $b_n=-frac{1}{pi n}$ 至此题目结束。

　　但是我想练习一下最近自己刚刚接触到的numpy和matplotlib，于是动手写了一个python小程序想看看拟合的效果是什么样的。效果图和代码如下。　　

import numpy as np
import matplotlib.pyplot as plt


x = np.linspace(0, 1, 100)
y_ = np.zeros_like(x)
y = x
y_ = y_ + 0.5
for n in range(1, 11):
    y_ = y_ - 1/np.pi/n * np.sin(2*np.pi*x*n)

plt.plot(x, y, label='y=x')
plt.plot(x, y_, label='approximation')

plt.xlabel('x')
plt.ylabel('y')

plt.title("CFS")
plt.legend()
plt.show()

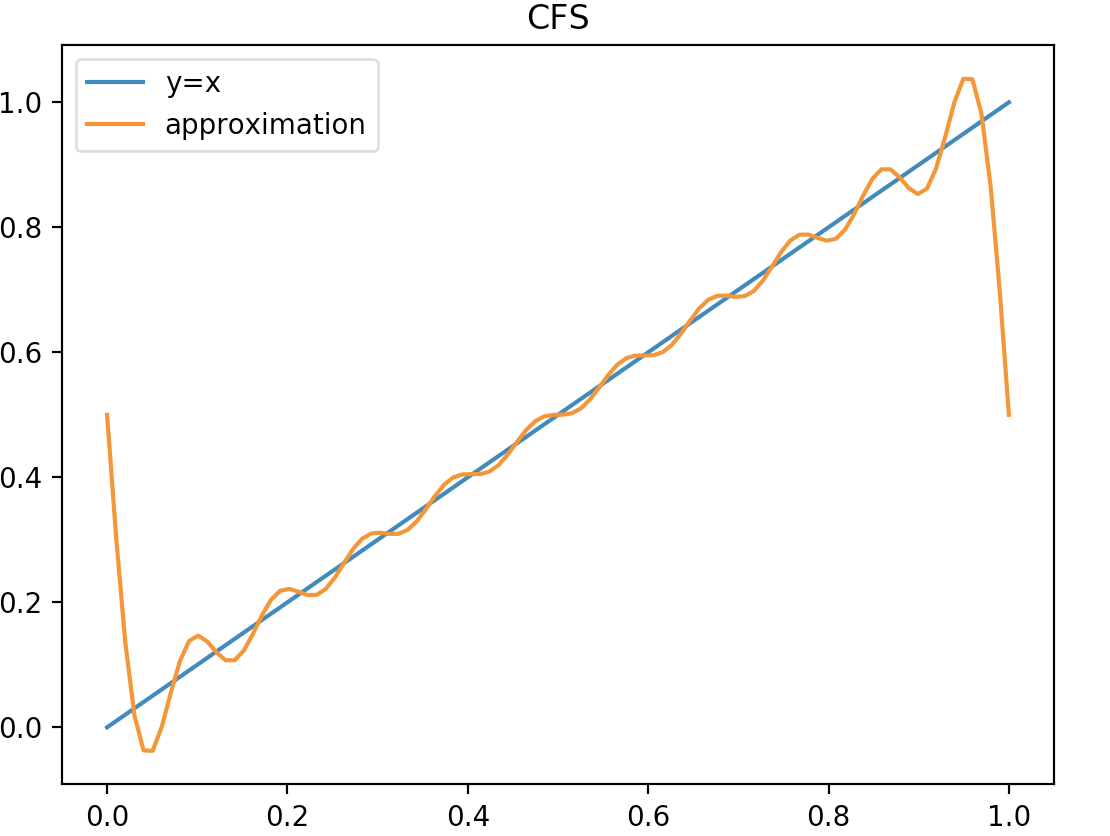
　　代码一直拟合到十阶分量。可看到效果还是不错的，增加x采样点可以增加图像平滑