DS博客作业07--查找

1.本周学习总结

思维导图

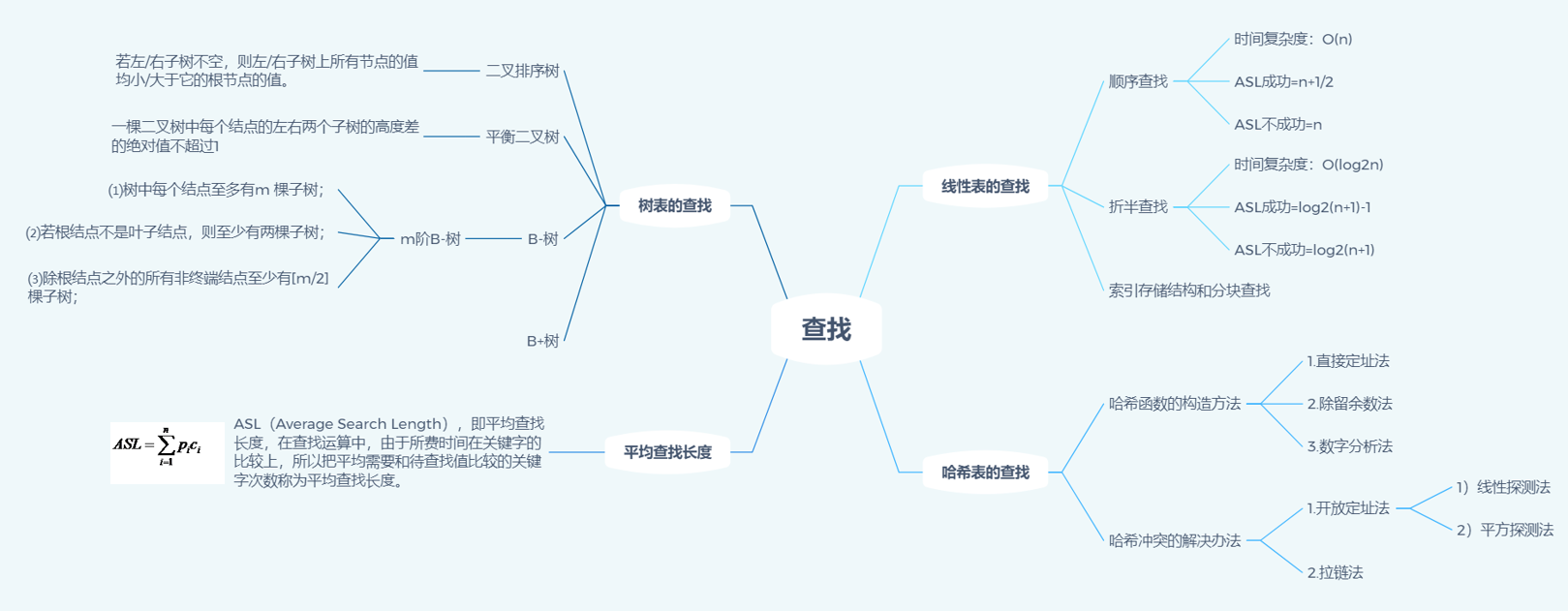
谈谈你对查找运算的认识及学习体会

在学习本章的知识前，我们得先掌握之前的二叉树的内容，这样才能顺利的掌握课本知识。在编程前要先想清楚思路再开始写代码，灵活地利用书上的知识。对于书上的算法代码,我们一定要仔细钻研每一步的具体含义和目的,在此基础上深入的了解算法的实现过程，在查找时利用书中给出的各种方法可以极大地减少时间复杂度，从而提高查找速度，使算法更加简单。很多时候单看书上的内容会觉得很简单，但是真正做起来又很容易忘东忘西，所以增加实际应用经验很重要。

2.PTA实验作业

2.1.题目1：QQ帐户的申请与登陆

实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是：据说现在的QQ号码已经有10位数了。

2.1.1设计思路

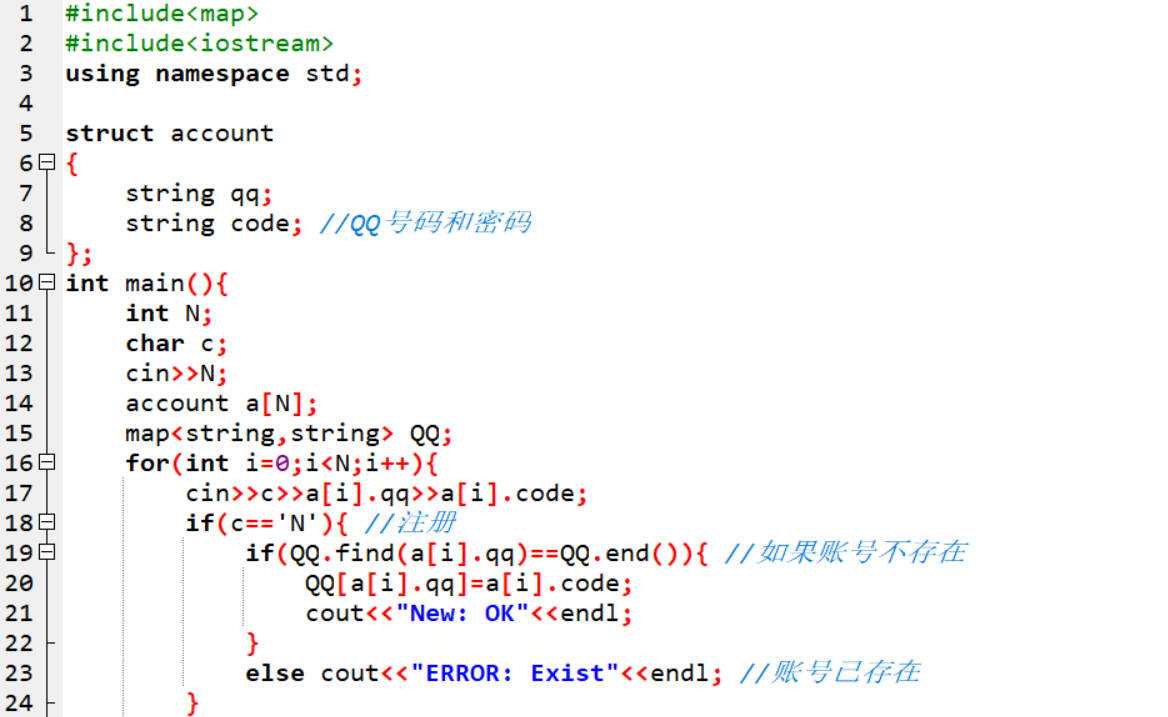
main函数{
定义整型数N；
定义字符 c；
输入N；
定义结构体数组a[N];
定义map QQ；
for i=0 to N
    输入c，a[i].qq，a[i].code；
    if 输入‘N’  //注册账号
        if QQ.find(a[i].qq)等于QQ.end() //map查找qq账号，如果账号不存在
            QQ[a[i].qq]=a[i].code；
            输出"New: OK"； //账号创建成功
        else 输出“ERROR: Exist”； //qq账号已存在，创建失败
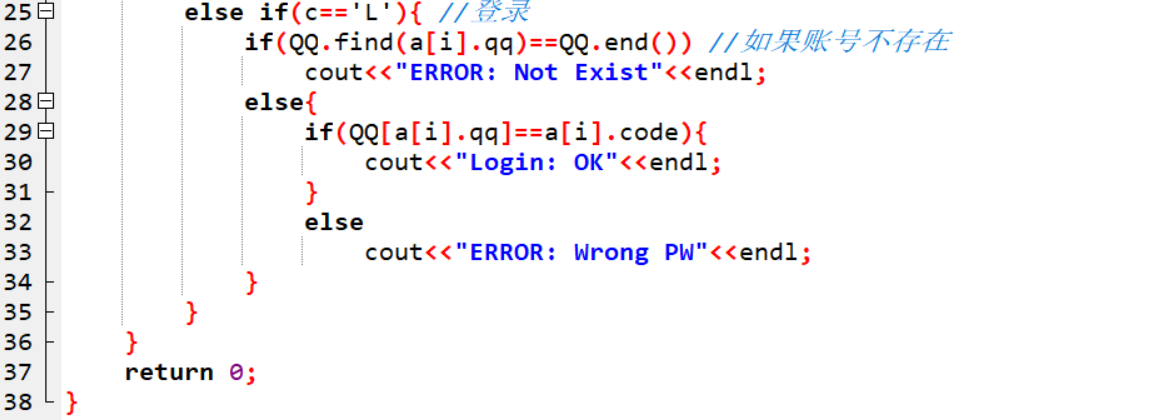
    else if 输入‘L’ //登录账号
    if QQ.find(a[i].qq)等于QQ.end()  //map查找qq账号，如果账号不存在 
        输出"ERROR: Not Exist"；
    else
        if QQ[a[i].qq]等于a[i].code  //如果账号和密码匹配成功 
            输出“Login: OK”；
        else
            输出“ERROR: Wrong PW”；

return 0；
        
}

2.1.2代码截图

2.1.3本题PTA提交列表说明

• 本来想的思路比较复杂，但后来发现用map会很简单。
• 在登录的那几行代码中因为if else语句叠了三层所以有些逻辑混乱，导致老是找不出错误原因。

2.2.题目2：二叉搜索树中的最近公共祖先

在一棵树T中两个结点u和v的最近公共祖先(LCA)，是树中以u和v为其后代的深度最大的那个结点。现给定某二叉搜索树(BST)中任意两个结点，要求你找出它们的最近公共祖先。

2.2.1设计思路

LCA函数{
定义两个树节点指针t，s；
定义一个flag；
if 树为空 返回 ERROR
while t不为空
    if 当前节点等于u
        flag++；
        break；
    else if 当前节点大于u 
        t等于它的左孩子
    else t等于它的右孩子
while s不为空
    if 当前节点等于v
        flag++；
        break；
    else if 当前节点大于v 
        t等于它的左孩子
    else t等于它的右孩子

if flag不等于2说明u，v有一个不在二叉树内，返回ERROR

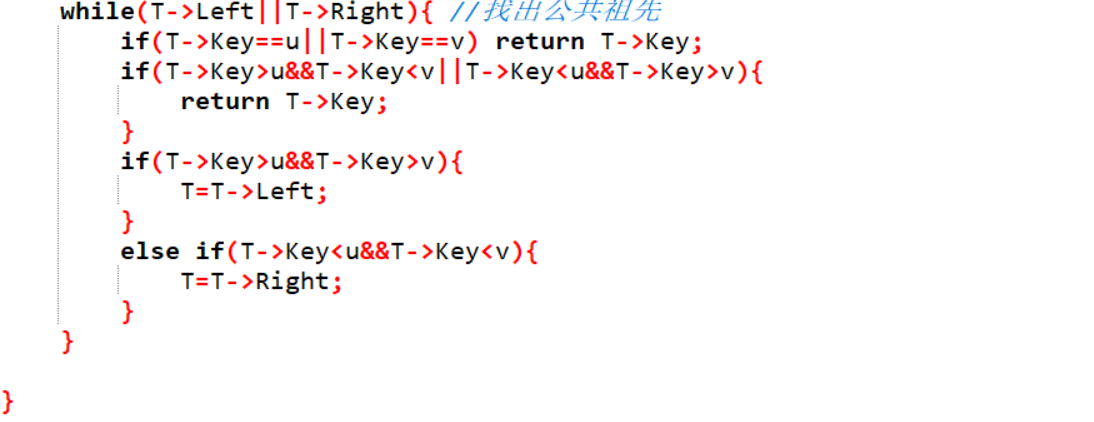
while T的左右孩子有一个不为空
    if T.Key等于u或者等于v 
        return T->Key；
    if T->Key大于u且T->Key小于v或T->Key小于u且T->Key大于v
        return T->Key；
    if T->Key 大于 u和v
        T等于它的左孩子；
    if T->Key 小于 u和v
        T等于它的右孩子；
}

2.2.2代码截图

2.2.3本题PTA提交列表说明

• Q1：刚开始提交只对了三个测试点，发现是检查u和v是否在二叉树的代码有误。
• A1：将两个循环中的else if语句中的条件修改了。
• Q2：当LCA是本身时的测试点过不去。
• A2：添加了补充条件后仍过不了，发现是总的循环条件写错了，导致只能遍历到左右孩子都有的节点，最后把&&改成||就对了。

2.3.题目3：二叉搜索树的操作集

本题要求实现给定二叉搜索树的5种常用操作。

2.3.1设计思路

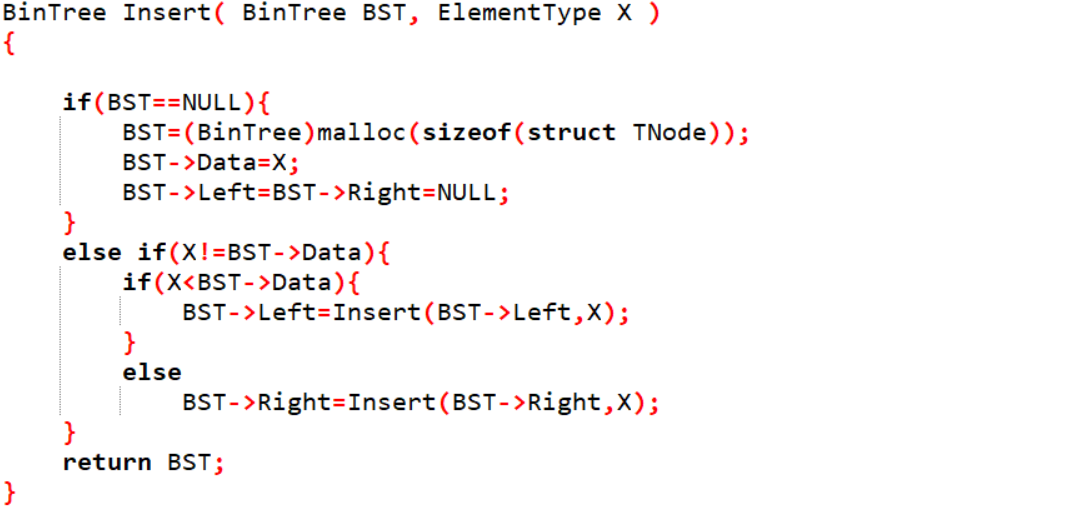
Insert函数{
    if BST为空
        BST->Data等于X；
        BST的左右孩子都置为空；
    else if X不等于BST->Data
        if X小于BST->Data
            BST->Left等于Insert(BST->left,X)；
        else
            BST->Left等于Insert(BST->left,X)；
return BST；
}

Delete函数{
定义树节点 q；
if BST为空 输出"Not Found
"；
else{
	if(X小于BST->Data)
		BST左孩子等于Delete(BST->Left,X);
	else if(X大于BST->Data)
	{
		BST右孩子等于Delete(BST->Right,X);
	}
	else  //考虑如果找到这个位置，并且有左节点或者右节点或者没有节点三种情况
        {
            if BST的左右孩子都在 {
                q=FindMin(BST->Right);  
                BST->Data=q->Data;
                BST->Right=Delete(BST->Right,BST->Data);
            }
            else
            {                                
                q=BST;
                if(左孩子为空) BST = BST->Right;       
                else if(右孩子为空) BST = BST->Left;
                释放q；                         
            }
       }
	}
	return BST;
}

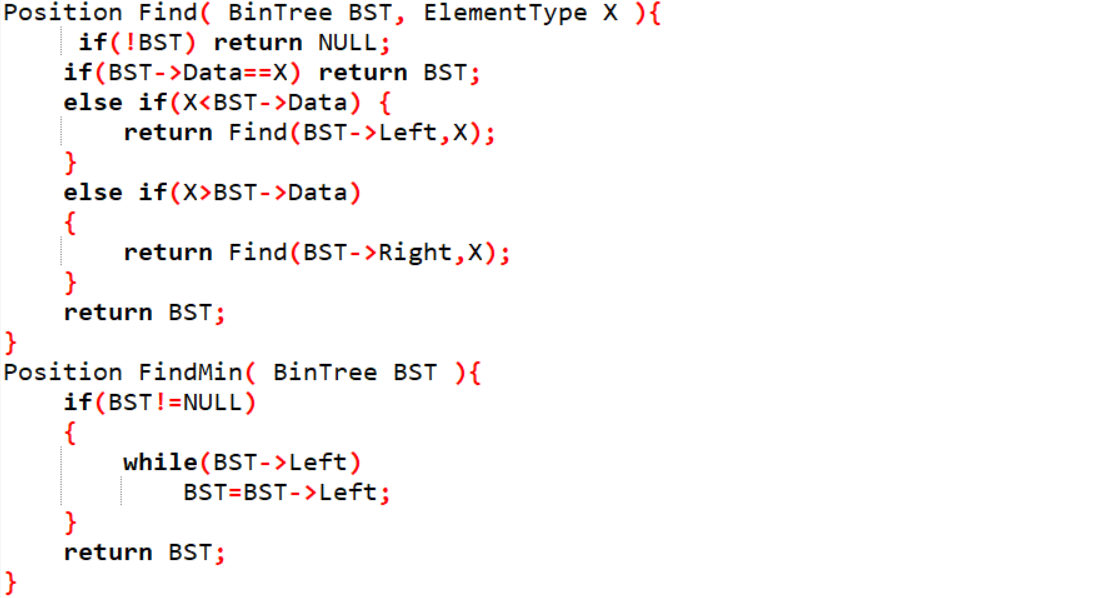
Find函数{
    if(BST为空) return NULL;
    if(BST->Data等于X) return BST;
    else if(X小于BST->Data) {
        return Find(BST->Left,X);
    }
    else if(X大于BST->Data)
    {
        return Find(BST->Right,X);
    }
    return BST;
}

FindMin函数{
    if(BST不为空)
    {
        while(BST的左孩子不为空)
            BST=BST->Left;
    }
    return BST;
}

FindMax函数{
    if(BST不为空)
    {
        while(BST的右孩子不为空)
             BST=BST->Right;
    }
    return BST;
}

2.3.2代码截图

2.3.3本题PTA提交列表说明

• 在写删除函数代码时，参考书上的思路会时自己的思路比较清晰

3.阅读代码

3.1 题目：是否完全二叉搜索树

3.2 解题思路

完全二叉树的定义是：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边。
因为右子树的结点编号是父节点的两倍，而左子树的结点编号是父节点的两倍加一，所以可以用数组模拟建树的过程。最后题目要求层序输出，直接按编号大小输出。而最后一行的结点编号和n相等。

3.3 代码截图

3.4 学习体会

本题定义了一个数组a来模拟建树的过程使代码变得更加简单，这要求要掌握完全二叉树的概念和性质，了解左子树的结点编号和它父结点的结点编号的关系。在判断是否为完全二叉树时，他巧妙地利用结点数和i来判断。当置数组a的初值时他用到了memset函数，但我们自己在使用memset时要千万小心，要知道在给char以外的数组赋值时，只能初始化为0或者-1。