If the degree of the numerator of a rational function is one greater than the degree of the denominator, the graph has an oblique(slanted)asymptote. We find an equation for the asymptote by dividing numerator by denominator to express f as a linear function plus a remainder that goes to zero as . Here is an example.

The function f(x) = x is called the identity function.
All composites of continuous functions are continuous.
The rules of exponents tell us that if a is any number different from zero. They also tell us that
if n is any positive number.
.
max { a, b } = (a+b)/2 + |a+b|/2
min { a, b } = (a+b)/2 - |a+b|/2

Answer:



Answer:


Answer:

At what points are the following functions continuous?
1.
2. 3.
Answer:
-
(k is any integer)
-
-
Lorentz contraction
In relativity theory, the length of an object, say a rocket, appears to an observer to depend on the speed at which the object is traveling with respect to the observer. If the observer measures the rocket's length as at rest, then at speed
the length will appear to be
.
This equation is the Lorentz contraction formula. Here, c is the speed of light in a vacuum.
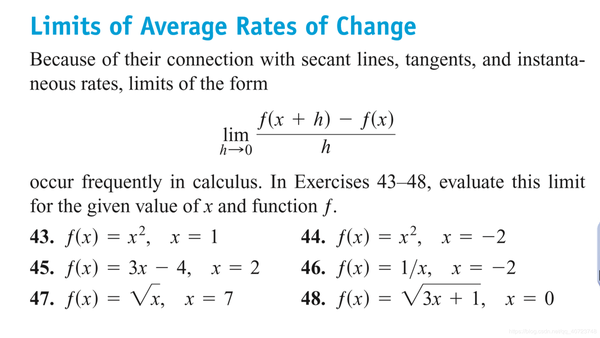
Answer:

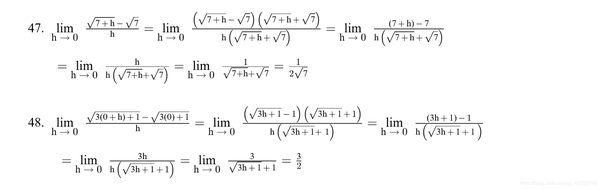
Graph the following curves, where do the graph appear to have vertical tangents? Confirm your findings with limit calculations.
Answer:







On what intervals are the following functions continuous?
Answer: