目录
一、预备知识
二、二叉树
三、查找树ADT-----二叉查找树
四、AVL树
五、伸展树
六、树的遍
七、B树
八、标准库中的集合与映射
对于大量的输入数据 ,链表的线性访问时间太慢,不宜使用。而树的大部分操作都是O(logN).这种结果就是二叉查找树,它是两种库
集合类 TreeSet /TreeMap 的基础。
一、预备知识
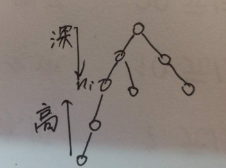
深度:从根到 ni的唯一 的路径长,根的深度是0。
高度:从ni到树叶的最长路径长。 树叶的高为0。一个树的高为它根的高。
- 树的实现
- 树的遍历和应用
先序遍历
对节点的处理在它的诸儿子节点处理前。如列出分级文件系统中目录的伪代码,效果如下:
private void listAll(int depth ){
printName(depth) ;
if (isDirectory())
for each file c in this dir(for each child)
c.listAll(depth+1);
}
public void listAll(){
listAll(0);
}
从深度为0开始。
中序遍历
先左,再中,再右,可以用于顺序的输出所有的项。
后序遍历
对节点的处理是在它的儿子节点被计算后再进行。如要计算每个文件的大小。
public int size(){
int totalSize = sizeOfThisFile();
if (isDirectory())
for each file c in this dir (for each child)
totalSize+=c.size();
return totalSize ;
}
二、二叉树
每个节点都不能有多于两个儿子。
二叉树的一个重要的性质:
一个平均二叉树的深度比节点个数 N小得多。平均深度为N开方。对于特殊的,也就是二叉查找树,平均深度为
O(logN).
class BinaryTree {
Object element ;
BinaryTree left ;
BinaryTree right;
}
二叉树有很多与搜索不相关的应用,如编译器设计 。
三、查找树ADT-----二叉查找树
二叉树一个重要 的应用是查找 。
要使二叉树成为二叉查找树,则:
对于树中的每个节点 X ,它的左子树中所有项目的值小于X,右子树中所有项的值 大于X的值。
二叉查找查要求所有的项目都可以排序。要写出一个一般 的类,就要有一个Comparebla 接口。
下面是代码文件,和链表中一样,BinaryNode是一个嵌套的类。
private static class BinaryNode <Anytype>{
Anytype element ;
BinaryNode<Anytype> left ;
BinaryNode<Anytype> right ;
BinaryNode(Anytype element ) {
}
BinaryNode(Anytype element , BinaryNode<Anytype> lt, BinaryNode<Anytype> rt ) {
this.element = element ;
this.left = lt ;
this.right = rt ;
}
}
下面是BinarySearchTree类的代码 。
package Tree;
public class BinarySearchTree <Anytype extends Comparable<? super Anytype>>{
private static class BinaryNode <Anytype>{
Anytype element ;
BinaryNode<Anytype> left ;
BinaryNode<Anytype> right ;
BinaryNode(Anytype element ) {
}
BinaryNode(Anytype element , BinaryNode<Anytype> lt, BinaryNode<Anytype> rt ) {
this.element = element ;
this.left = lt ;
this.right = rt ;
}
}
private BinaryNode< Anytype> root ;
public BinarySearchTree(){
root = null;
}
public void makeEmpty (){
root = null ;
}
public boolean isEmpty (){
return root==null ;
}
public boolean contains(Anytype x){
return contains(x, root ) ;
}
public Anytype findMin () throws Exception{
if (isEmpty())
throw new Exception() ;//should be UnderflowException
return findMin (root).element;
}
public Anytype findMax () throws Exception{
if (isEmpty())
throw new Exception() ;
return findMax(root ).element ;
}
public void insert (Anytype x ){
insert(x, root) ;
}
public void remove (Anytype x ){
remove(x, root );
}
/**
* 没完成
*/
private boolean contains(Anytype x , BinaryNode<Anytype> t ){
return true ;
}
private BinaryNode<Anytype> findMin (BinaryNode<Anytype> t){
return null ;
}
private BinaryNode<Anytype> findMax (BinaryNode<Anytype> t){
return null ;
}
private BinaryNode<Anytype> insert (Anytype x , BinaryNode<Anytype> t ){
return null ;
}
private BinaryNode<Anytype> remove(Anytype x, BinaryNode<Anytype> t ){
return null ;
}
private void printTree (BinaryNode<Anytype> t ){
}
}
- contains方法
代码如下:
private boolean contains(Anytype x , BinaryNode<Anytype> t ){
if (t == null){
return false ;
}
int result = x.compareTo(x) ;
if (result<0){
return contains(x,t.left) ;
}else if (result>0){
return contains(x , t.right) ;
}else {
return true ;
}
}
这里使用的是尾递归。可以用一个while循环代替,不过这里使用栈的空间量也不过是 O(logN)而已,没有大的问题。
下面是一种使用函数对象而不是要求这些 项是 Comparable 的方法。(省)
- findMax与finaMin方法
findMax:只要有右儿子就向右进行。
findMin :只要有左儿子就向左进行。
我们一种用递归 ,一种不用递归写。
private BinaryNode<Anytype> findMin (BinaryNode<Anytype> t){
if (t== null){
return null ;
}else if ( t.left==null) {
return t;
}
return findMin(t.left) ;
}
private BinaryNode<Anytype> findMax (BinaryNode<Anytype> t){
if (t!=null){
while (t.right!=null)
t= t.right ;
}
return t ;
}
- insert方法
可以像contains那样查找 (实际就是一次遍历)
1.如果找到,什么也不用做。
2.如果没有,则将X插入到遍历路径的最后 一个点上。
由于t 引用树的根,而根在第一次插入时变化 ,因此 insert返回的是新树的根。
如下:
private BinaryNode<Anytype> insert (Anytype x , BinaryNode<Anytype> t ){
if (t== null){
return new BinaryNode<Anytype>(x, null,null) ;
}
int result = x.compareTo(t.element) ;
if (result<0){
t.left = insert(x, t.left) ;
}else if (result>0) {
t.right = insert(x, t.right) ;
}else {
//重复,不处理
}
return t;
}
- remove方法
和很多数据结构一样,最复杂 的是删除操作。
如果删除的节点是:
1.一个树叶:直接删除。
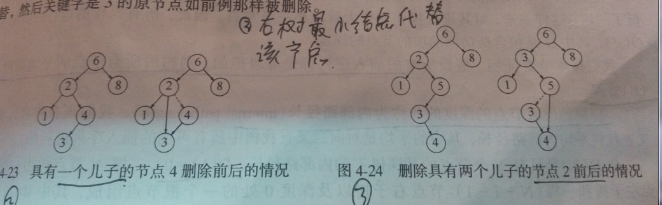
2.有一个儿子:这个节点可以在其父亲节点调整自己的链以绕过自己后删除 。
3.有两个儿子:用其右子树最小的节点(容易找到)代替这个节点的数据,并递归的删除那个节点(现在它是空的)。因为右
树中最小的节点不可能 有左儿子,所以第二次remove很容易。
注意3中,因为总是用右子树的节点来代替被 删除的节点 ,所以倾向于使械子树比右子树高。
下面是代码 ,但是效率并不是很高,因为它对树进行两次搜索以查找 和删除右子树中最小的节点 ,通过写一个removeMin()可以解决这个问题。
我们先不考虑这个 。
private BinaryNode<Anytype> remove(Anytype x, BinaryNode<Anytype> t ){
if (t== null) return t ;
int result = x.compareTo(t.element) ;
if (result<0){
t.left = remove(x, t.left) ;
}else if (result>0) {
t.right = remove(x, t.right) ;
}else if (t.left!= null && t.right!= null) {
//用其右子树最小的节点(容易找到)代替这个节点的数据
t.element = findMin(t.right).element ;
//并递归的删除那个节点(现在它是空的)
t.right = remove(t.element, t.right) ;
}else {
//只有一个儿子,这个节点可以在其父亲节点调整自己的链以绕过自己后删除
t = (t.left!= null) ? t.left: t.right ;
}
return t;
}
如果 删除的元素不多,我们使用的是惰性删除,也就是并没有真的删除元素,只是标记被删除的元素。这种特别是在有重复项的时候很适用,只用将频率减1。
- 平均情况分析
如果所有 的插入序列都是等可能 的,则树的所有节点的平均深度为O(logN)。
如果一个树的输入预先进行了排序 ,则一连串的insert操作将会花费二次的时间。而链表的实现代价会非常的大,因为这时树只有右儿子。一
一种解决的办法就是,让任何节点的深度都不能过深。(平衡树?)
下面要引入的是一个很古老的平衡查找树-AVL。
另外 一种比较新的方法是放弃平衡条件,允许树有任意的深度,但是每次操作后用一定的规则进行调整,使后面的效率更高。这种是自调整结构。在二叉查找树下,我们不再保证 O(logN)的时间界,但是可以证明任意M次操作,复杂度为O(MlogN).
四、AVL树
AVL树是带有平衡条件的树二叉查找树。这个平衡条件要容易保持 ,而且能够保证树的深度是O(logN).
一个AVL树是每个节点的左子树和右子树高度最多相差1 的二叉查找树(空树的高度-1)。一个实际的AVL树的高度只略大于logN. 是
除了可能插入外(假设是惰性删除),所有的树的操作都 可以在O(logN)里完成。插入可能会破坏AVL树的特性,这个问题可能通过旋转来搞定 。
只有那些从插入点到根节点路径上的点的平衡性才有可能变化。称要重新平衡的节点为A,出现不平衡就要A点的两个子树的高度差2.有以下几种情况 :
1、对A点的左儿子的左子树进行一次插入。
2、对A点的左儿子的右子树进行一次插入。
3、对A点的右儿子的右子树进行一次插入。
4、对A 点的右儿子的左子树进行一次插入。
理论上只有两种,编程上看有四种。理论上看:
第一种:发生在外边,(左-左,右-右),可以通过单旋转解决。
第二种:发生在内边,(左-右,右-左),可能 通过双旋转处理。
上面处理都是对树的基本操作。将会用在别的平衡算法中。
- 单旋转
如下图示,这里出现了情况 都是外边情况。
插入3,2,1,在1时出现了问题。

插入4时没有问题,5时节点3处有问题。

插入6时,根节点处左子树高度是0,右子树高度是2.
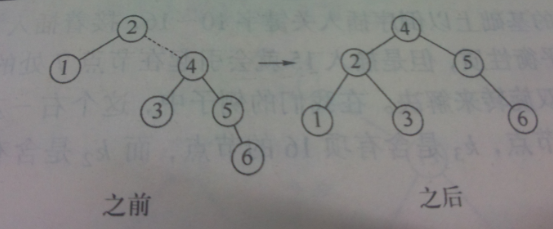
插入7时有问题。
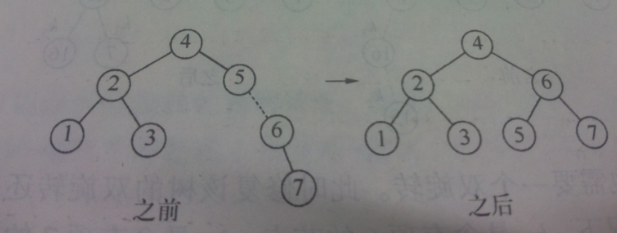
- 双旋转
上面的对于下图的情况没有作用。
当在上面的基础上插入16, 15时,出现不平衡。
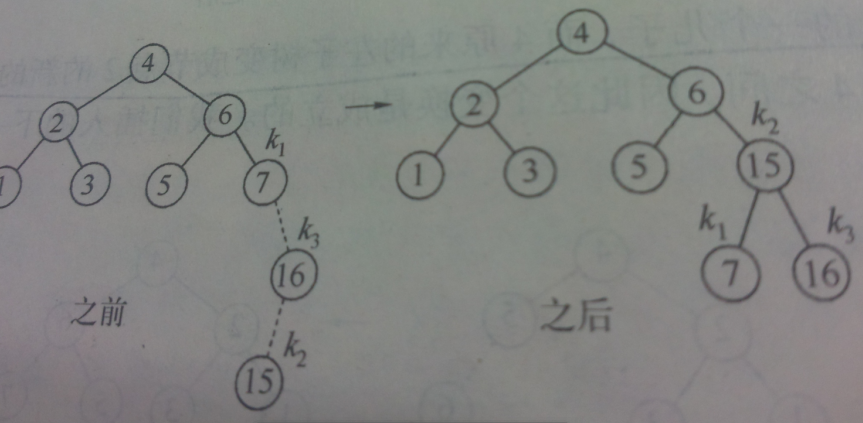
再插入14时,出现不平衡
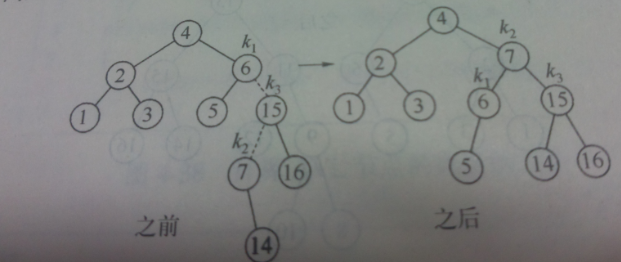
经过上面的分析 ,我们总结出,为将一个新的结点X插入到T中,我们递归的将X插入到T相应的子树(TrL)中,并更新高度。
如果子树高度不变,则完成。
如果子树高度变化,则要进行调整。
- AVL树的节点 声明
private static class AvlNode <Anytype>{
Anytype element ;
int height ;
AvlNode<Anytype> left ;
AvlNode<Anytype> right ;
AvlNode(Anytype element ,AvlNode<Anytype> right, AvlNode<Anytype> left ){
this.element = element ;
this.left = left ;
this.right = right ;
}
AvlNode(Anytype element){
this(element, null, null) ;
}
}
我们要有一个快速的返回高度的方法,同时要处理null引用的问题。
private int height(AvlNode<Anytype> t ){
return t== null? -1: t.height ;
}
- 单旋转方法
第一种是左旋转,如下图
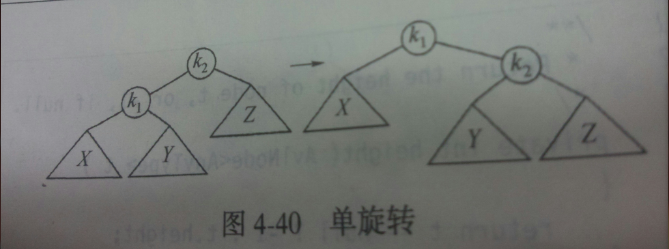
/**
* single rotate for case 1
* there should be a method rotateWithRightChild
* @param k2
* @return new root
*/
private AvlNode<Anytype> rotateWithLeftChild(AvlNode<Anytype> k2){
AvlNode<Anytype> k1 = k2.left;
k2.left = k1.right ;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right))+1;
k1.height= Math.max(height(k1.left), k2.height)+1;
return k1 ;
}
- 双旋转方法
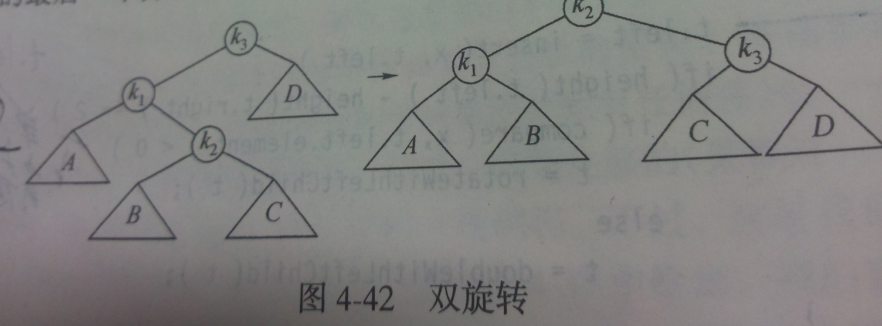
/**
* first left child with its right child
* then node k3 with new left child
* @param k3
* @return
*/
private AvlNode<Anytype> doubleWithLeftChild(AvlNode< Anytype> k3 ){
k3.left = rotateWithRightChild(k3.left) ;
return rotateWithLeftChild(k3) ;
}
AVL树的删除更加复杂 ,不过如果 删除比较少,可以用惰性删除。
五、伸展树
六、树的遍历
七、B树
八、标准库中的集合与映射