目录
一、散列函数
二、分离链接法
三、不用链表的散列表
四、再散列
五、标准库中的散列表
六、可扩散列
七、小结
散列表的实现通常叫作散列,是一种用于以常数时间完成 insert, delete ,find的技术,但是任何需要元素的排序信息的操作都不支持,如
findMin, findMax ,按排序打印元素等。
一、散列函数
一个比较好的散列函数如下,但是如果关键字过长,则计算时间会有些长,这样时我们不使用所有的字符,比如只使用奇数位。这里有这样一种
想法,用计算散列函数节约下来的时间来补偿产生的对均匀分成 函数的影响。
/**
* a hash rountine for String objects
* 37=26+space+number
* @param key
* @param tableSize
* @return
*/
public static int hashCode(String key , int tableSize){
int hashVal =0;
for (int i =0;i<key.length(); i++){
hashVal =37*hashVal+key.charAt(i);
}
hashVal %= tableSize ;
if (hashVal<0){ //溢出
hashVal+= tableSize ;
}
return hashVal ;
}
剩下的主要编程细节是解决冲突的问题,也就是一个元素插入时与一个已经插入的元素散列到同一个值。有两个方法,分离链接法和开放定址法。
二、分离链接法
做法是将散列到同一个值的所有的元素都保存到一个表中。这个表可以用标准单元库的表(双链表)来实现 ,但是占空间较大,所以我们可以自己用单向链表实现。
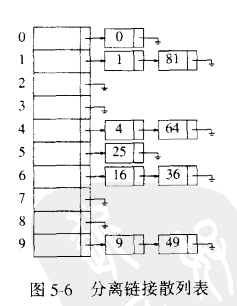
上面假设散列函数是 hash(x) = x mod 10。(从这里可以看到,最好保证表的大小是素数,如下面代码 中的101)。
查找:先用散列值确定遍历那条链,再在确定的链表中查找到元素。
插入:查看相应的链表是否已经 有这个元素,如果没有,插入到链表的最前端,这不仅方便,还是因为,最新插入的元素最有可能不久会被访问。
分离链接法实现如下,散列表保存一个链表数组。
package charpter5;
import java.util.LinkedList;
import charpter3.List;
public class SeparateChainHashTable <AnyType>{
private static final int DEFAULT_TABLE_SIZE=101 ;
private List<AnyType> [] theLists ;
private int currentSize ;
public SeparateChainHashTable(){
this(DEFAULT_TABLE_SIZE) ;
}
public SeparateChainHashTable(int size ){
theLists = (List<AnyType>[]) new LinkedList [nextPrime(size)] ;
for (int i =0;i<theLists.length;i++)
theLists[i] = (List<AnyType>) new LinkedList<AnyType>() ;
}
public void insert (AnyType x){
List<AnyType> whichList = theLists[myhash(x)] ;
if (!whichList.contains(x)){
whichList.add(x) ;
//查看 是否要扩大散列表
if (++currentSize> theLists.length)
rehash() ;
}
}
public void remove (AnyType x ){
List<AnyType> whichList = theLists[myhash(x)] ;
if (whichList.contains(x)){
whichList.remove(x) ;
currentSize-- ;
}
}
public boolean contains(AnyType x ){
List<AnyType> whichList = theLists[myhash(x)] ;
return whichList.contains(x) ;
}
public void makeEmpty (){
for (int i=0; i<theLists.length ;i++){
theLists[i].clear();
}
currentSize =0;
}
private void rehash(){
}
private int myhash (AnyType x){
int hashVal = x.hashCode() ;//类自己的hashCode
hashVal %= theLists.length ;
if (hashVal<0)
hashVal += theLists.length ;
return hashVal ;
}
/**
*size 下一个素数
* @param n
* @return
*/
private static int nextPrime(int size ){
return 0;
}
private static boolean isPrime (int n){
return true ;
}
}
像二叉树只对那些是Comparable的对象工作一样,散列表只对提供了equals / hashCode的方法适用,散表表将hashCode结果通过myhash软件成适当的数组下标。
在插入的时候,如果已经存在 ,则什么都不做,如果不存在 ,将元素放入其中,这个元素可以被放到任意位置,我们用add最方便。
除链表外,别的方案也可以解决冲突,如二叉树等,但是我们希望所有的链表都是短的,所以其它 任何复杂的想法都不用考虑了。
分离链表的缺点
使用了链表,给新的单无分配地址要时间,特别是在个别语言中,导致算法速度慢,同时算法实际上还要第二种数据结构实现 (链表)。
下面是不用链表解决冲突的方法,尝试别的单元,直到找到空的单元为止。h(x)= (hash(x)+f(i)) mod tablesize.这种表叫做探测散列表,装填因子低于
0.5,比用分离链表时大。
三、不用链表的散列表
- 线性探测法
f(i)=i
占据的单元 容易 形成一些 区块,这种 就是一次聚集。
- 平方探测法
f(i)=i*i
对于线性探测表,让散列表几乎放满元素不是个好主意,会让表的性能 降低很多。
对于平方探测更是如此,当表填充超过一半时,如果表的大小 不是素数,甚至在表被填充一半前,就不能保证 一次能找到空的单元了。
定理:如果是平方探测,且表的大小是素数,当表至少有一半是空的时候 ,总能够插入一个新的元素。
在线性探测散列表中,标准的删除操作不可行,只能进行惰性删除,因为删除一个元素后,可能剩下的contains操作都会失败。
下面是平方探测法的例子:
package charpter5;
public class QuadicProbingHashTable <AnyType>{
private static class HashEntry <AnyType>{
public AnyType element ;
public boolean isActive ; //false if deleted
public HashEntry(AnyType e ){
this(e, true) ;
}
public HashEntry(AnyType e , boolean i){
element = e;
isActive = i;
}
}
private static final int DEFAULT_SIZE=11;
private HashEntry<AnyType> [] array ; //1:null,2:不是null,active,3....
private int cuurentSize ;
public QuadicProbingHashTable(){
this(DEFAULT_SIZE) ;
}
public QuadicProbingHashTable(int size ){
allocateArray(size) ;
makeEmpty() ;
}
public void makeEmpty (){
cuurentSize=0;
for (int i=0; i<array.length;i++){
array[i]= null ;
}
}
public boolean contains(AnyType x ){
int currentPos = findPos(x) ;
return isActive(currentPos );
}
/**
* 如果装填因子 大于0.5,则进行扩大,这样就是再散列
* @param x
*/
public void insert (AnyType x ){
int currentPos = findPos(x) ;
if (isActive(currentPos))
return ;//元素已经存在
array[currentPos] = new HashEntry<AnyType>(x, true);
//rehash
if (++currentSize> array.length/2){
rehash() ;
}
}
public void remove (AnyType x){
int currentPos = findPos(x);
if (isActive(currentPos))
array[currentPos].isActive = false ;
}
private void allocateArray (int arraySize){
array = new HashEntry[arraySize];
}
private boolean isActive (int currentPos){
return array[currentPos]!=null && array[currentPos].isActive ;
}
/**
* 解决冲突的问题
* 下面的计算ith的方法比较快,因为没有用到乘法,如果越过数组大小 ,可以减去 length
*/
private int findPos (AnyType x ){
int offset =1;
int currentPos = myhash(x) ;
//下面的判断顺序不可变,判断 是不为空,且位置冲突 情况
while (array[currentPos]!=null &&
!array[currentPos].element.equals(x)) {
currentPos += offset ; //get ith probe,f(i)=f(i-1)+2i-1
offset+=2;
if (currentPos>= array.length){
currentPos-= array.length;
}
}
return currentPos;
}
private void rehash(){
}
private int myhash(AnyType x ){
return 0;
}
private static boolean isPrime (int n){
return true ;
}
}
虽然平方探测没有一次聚集,但是散列到同一个位置上的那些元素将会探测相同 的备选 单元 ,这叫二次聚集。下面的技术(双散列)将排除这个问题。(略)
四、再散列
对于使用平方探测的开放地址的散列法,如果散列表太满,则操作运行的时间就会要很长,且插入操作有可能失败。我们这里可以建立一个新的原来两倍的散列表。将没有删除的元素放到新表中。
这种操作是再散列,由于在再散列前已经存在了N/2次的insert ,因此添加到每个插入上的操作是一个常数开销。对速度的影响是不明显的。
有三种方法实现 :
1.只要表到一半满,就再散列。
2.当出现 插入失败时,再散列。
3.当装填因子到一定时进行再散列。
我们选择第三种。
private void rehash(){
HashEntry<AnyType> [] oldArray = array ;
allocateArray(nextPrime(2*oldArray.length)) ;
currentSize=0;
//copy table over
for (int i=0;i<oldArray.length;i++)
if (oldArray[i]!= null && oldArray[i].isActive)
insert(oldArray[i].element) ;
}
对于分离链表散列表的同散列,是类似的情况 。如下
private void rehash(){
List<AnyType> [] oldLists = theLists ;
//create double table
theLists = new List[2*nextPrime(oldLists.length)] ;
for (int i=0;i< theLists.length;i++){
theLists[i]= (List<AnyType>) new LinkedList<AnyType>();
}
//copy to new table
for (int i=0;i<oldLists.length;i++){
for (AnyType item :oldLists[i]){
insert(item) ;
}
}
}
五、标准库中的散列表
包括Set 和Map的散列表实现 ,也就是 HashSet /HashMap.它们中的项一定要有 equals、hashcode方法的实现 。且通常是用的分离链表实现的。
HashMap的性能常常比TreeMap的性能更好。
String类有一个技巧,闪存散列代码。就是将hashcode保存在类的一个字段中。
六、可扩散列
主要会对数据太多,装不进主存的情况,这里主要考虑的是读取磁盘的次数。(p142)
七、小结
散列表可以用常数时间来完成插入和查找操作。
- 散列表与二叉查找树比较
二叉查找树也可以用来实现 insert/contains操作,虽然平均时间为O(logN),但是二叉查找树支持需要排序的一些更加强大的功能。
使用散列表不可能找出最小元素等。
除非准确的知道一个字符串,否则不能有效的查找到它。而二叉查找树可以找到一定范围内的所有项。
此外,O(logN)也不一定比O(1)大很多,这是因为查找 树不要乘法和除法。
如果不要求有序的信息,就应该选择散列表。