| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(1) | 是 |
| 选择排序 | O(n²) | O(n²) | O(1) | 不是 |
| 插入排序 | O(n²) | O(n²) | O(1) | 是 |
| 快速排序 | O(nlogn) | O(n²) | O(logn) | 不是 |
| 希尔排序 | O(nlogn) | O(n^s) | O(1) | 不是 |
冒泡排序
最基本的排序算法,它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
function bubbleSort(arr) {
let N = arr.length
let swiper //标记是否完成排序
do{
swiper = false
for(let i=1;i<N;i++){
if (arr[i-1]>arr[i]) {
let temp = arr[i-1]
arr[i-1]=arr[i]
arr[i]=temp
swiper=true
}
}
N--
}while(swiper)
}
选择排序
表现最稳定的排序算法之一(这个稳定不是指算法层面上的稳定哈,相信聪明的你能明白我说的意思2333),因为无论什么数据进去都是O(n²)的时间复杂度.....所以用到它的时候,数据规模越小越好
function slectionSort(arr) {
for(let i=0;i<arr.length;i++){
minj=i; //标记最小值
for(let j =i+1;j<arr.length;j++){
if (arr[j]<arr[minj]) {
minj = j
}
}
if (minj!=i) {
let temp=arr[i]
arr[i]=arr[minj]
arr[minj]=temp
}
}
return arr;
}
插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
function insertionSort(arr) {
for(let i=1;i<arr.length;i++){
const key = arr[i]
let j
for(j=i-1;(j>=0)&&arr[j]>key;j--){
arr[j+1]=arr[j]
}
arr[j+1]=key
}
return arr;
}
快速排序
选择一个元素作为基数(通常是第一个元素),把比基数小的元素放到它左边,比基数大的元素放到它右边(相当于二分),再不断递归基数左右两边的序列。快速排序是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高! 它是处理大数据最快的排序算法之一了。
写法1
写法简洁,但不易懂
举例说明
例如对以下10个数进行排序: 6 1 2 7 9 3 4 5 10 8
- 以6为基准数(一般情况以第一个为基准数)
- 在初始状态下,数字6在序列的第一位,我们第一轮的目的是将6移动到一个位置(K),使得K左边的数都<6,K右边的数字都>=6。
- 为找到
K的位置,我们需要进行一个搜索过程,从右往左查找一个小于6的数字,位置为j,并将j处的值赋给i处 - 从左往右查找一个大于等于6的数字,位置为i,并将
i处的值赋给j处。 j和i的位置继续移动,重复3、4步骤。- 当
!(i<j)时,i的位置就是位置K,将位置K的数组和6交换。此时6左边的数字都被6小,6右边的数字都比6大或者相等。 - 将6左边和右边的序列进行上述操作。
function QuickSort(D, low, high) {
let i
let j
let s
while (low<high) {
i= low
j=high
s=D[low]
while (i<j) {
while (D[j]>s) {
j--
}
D[i]=D[j]
while (D[i]<=s && i<j) {
i++
}
D[j]=D[i]
}
D[i]=s
bubbleSort3(D,low,i-1)
low=i+1
}
}
function quicksort(D) {
QuickSort(D, 0, D.length - 1);
}
写法2
更易看懂的写法,相对来说比较好理解。
举例说明
例如对以下10个数进行排序: 6 1 2 7 9 3 4 5 10 8
- 以6为基准数(一般情况以第一个为基准数)
- 在初始状态下,数字6在序列的第一位,我们第一轮的目的是将6移动到一个位置(K),使得K左边的数都<=6,K右边的数字都>=6。
- 为找到K的位置,我们需要进行一个搜索过程,从右往左查找一个大于6的数字,位置为j,从左往右查找一个小于6的数字,位置为i,交互j和i上面的数字。
- j和i的位置继续移动,重复3步骤。
- 当j和i相等时,停止移动,移动到的位置就是位置K,将位置K的数组和6交换。此时6左边的数字都被6小,6右边的数字都比6大。
- 将6左边和右边的序列进行上述操作。
function bubbleSort3(D,low,high){
if(low > high) return D
let temp = D[low]
let i = low
let j = high
while(i!=j){
while(D[j]>=temp && j>i){
j--
}
while(D[i]<=temp && j>i){
i++
}
if (j>i) {
[D[i],D[j]]=[D[j],D[i]]
}
}
[D[low],D[i]]=[D[i],temp]
// console.log(`${D[i]}作为基准点:`, D);
bubbleSort3(D,low,i-1)
bubbleSort3(D,i+1,high)
return D
}
快排优化-三路快排
相较于上面我们提到的经典快排,我们可以有更为快速的快排方法三路快排。接下里我们就配合着图我们来讲解:
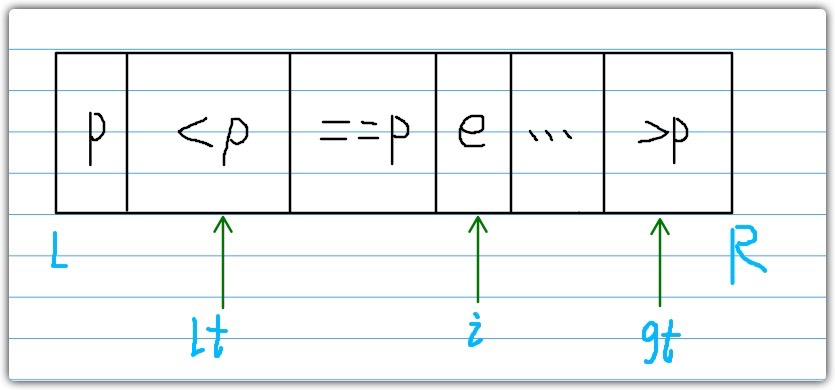
排序一开始这些区间是不存在的,在不断的深入的情况下,这三个区就会逐渐出来。我们来解释一下各个区是干什么的的吧:
- 我们设置开头第一个数
P为基准值,以此来比较 <P的区域则是将小于基准值的值放在这边==p的区域我们是将等于基准值的值放在这里e则是我们根据i不断前进指向的数组值···则是还未开始排序的值>P是将大于基准值的放在这理
所以,我们将整个数组大致分为三部分,[L,lt-1]为小于基准值、[lt+1,i-1]为等于基准值、[gt,R]为大于基准值
大致思路
例如对以下10个数进行排序: 6 1 2 7 9 3 4 5 10 8
- 以
6为基准数,L = 数组起点,lt = L,i = L+1,R = 数组结尾,gt = R+1 - 使用
i所指的1对比基准值,小于基准值,则lt+1 与 i相交换,也就相当于自己换自己。i++,lt++ 2小于基准值,执行第2步7大于基准值,将[gt-1] 与 i相交换。gt--- 由于上一步
i并未改变,8大于基准值,执行第4步 - 就这样不断循环,直到
i == gt时推出循环,之后将[lt] 与 L相交换。并且lt--
代码
const partition = function (arr, L, R) {
// 基准值为数组的零号元素
let p = arr[L];
// 左区间的初始值: L
let lt = L;
// 右区间的初始值: R+1
let gt = R + 1;
for (let i = L + 1; i < gt;){
if(arr[i] === p){
// 当前i指向的元素等于p
i++;
} else if(arr[i] > p){
// 当前i指向的元素大于p,将gt-1处的元素与当前索引处的元素交换位置,gt--
[arr[gt -1],arr[i]] = [arr[i],arr[gt - 1]];
gt--;
}else{
// 当前i指向的元素小于p,将lt+1处的元素与当前索引处的元素交换位置,lt+1,i+1
[arr[lt + 1],arr[i]] = [arr[i],arr[lt + 1]];
lt++;
i++;
}
}
// i走向gt处,除了基准值外的元素,其余的空间已经分区完毕,交换基准值与lt处的元素,lt-1,最终得到我们需要的三个区间
[arr[L],arr[lt]] = [arr[lt],arr[L]];
lt--;
console.log(`三路快排后的数组: ${arr}`);
return {lt : lt, gt : gt};
}
const threeWayFastRow = function (arr,L,R) {
// 当前数组的起始位置大于等于数组的末尾位置时退出递归
if(L >= R){
return false;
}
let obj = partition(arr, L, R);
// 递归执行: 将没有大于p,和小于p区间的元素在进行三路快排
threeWayFastRow(arr,L,obj.lt);
threeWayFastRow(arr,obj.gt,R);
}
//测试
console.time("三路快排");
const dataArr = [3,5,8,1,2,9,4,7,6];
threeWayFastRow(dataArr,0,dataArr.length - 1);
console.log(`三路快排完成: ${dataArr}`);
console.timeEnd("三路快排");
希尔排序
通过某个增量 gap,将整个序列分给若干组,从后往前进行组内成员的比较和交换,随后逐步缩小增量至 1。希尔排序类似于插入排序,只是一开始向前移动的步数从 1 变成了 gap。
const shellSort = function(arr){
const N = arr.length
//最外层循环,用来对得到gap
for(let gap = N;gap = parseInt(gap/2);){
///第二层循环,用来以gap为增量,在数组中向前查看值
for(let i= gap; i<N;i++){
//将当前查看的值进行保存
const k = arr[i]
let j
//第三层循环,用来当前查看的值与以gap为间隔从后往前的比较大小
for(j= i;j>=gap&&arr[j-gap]>k;j-=gap){
arr[j]=arr[j-gap]
}
arr[j]=k
}
}
}
搬运文章
[算法可视化](