题目大意:给定一个无向图,点i处有Ai头牛,点i处的牛棚能容纳Bi头牛,求一个最短时间T使得在T时间内所有的牛都能进到某一牛棚里去。(1 <= N <= 200, 1 <= M <= 1500, 0 <= Ai <= 1000, 0 <= Bi <= 1000, 1 <= Dij <= 1,000,000,000)
题解:首先二分答案T,然后变为限制问题。对于每一对距离不大于T的牛棚我们引流,同时对于每一个牛棚限源Ai,限汇Bi,然后我们就Wa了。
为什么呢?我们可以画个图:
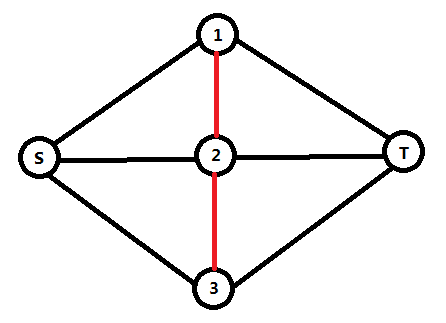
在这个图中我们假设dist[1,2],dist[2,3]都不大于T,而dist[1,3]大于T,那么我们应该只连[1,2],[2,3]对吧?可是看这个图我们发现1也可以到3,我们的限制条件就失效了= =
引流太乱我们就拆点好了,就A了。
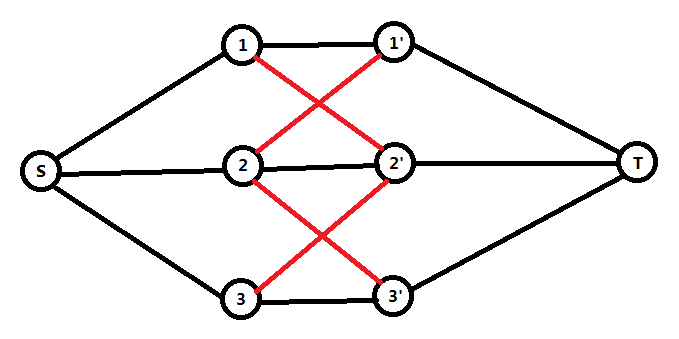
注意好是无向图。