[NOI2006]网络收费

题面在这里

description

一棵(2^n)个叶节点的满二叉树,每个节点代表一个用户,有一个预先的收费方案(A)或(B);
对于任两个用户 (i,j(1≤i<j≤2^n)i,j(1≤i<j≤2^n)),首先在树上找到与它们距离最近的公共祖先(P)，然后观察(P)所管辖的叶结点（即用户）中选择付费方式(A)与(B)的人数，分别记为(n_A)与(n_B) ，接着按下表进行收费，其中(F_{i,j})为(i)和(j)之间的流量，且为已知量。

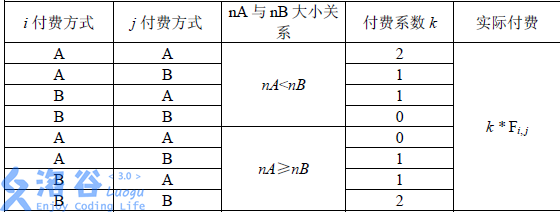
给定每个用户注册时所选择的付费方式以及修改收费方案的费用(C_i)((A)修改为(B),(B)修改为(A))，试求这些用户的最小费用

data range

[nle 10,F_{i,j}le 500,C_ile 500000 ]

solution

技不如人,甘拜下风

一开始看错了题目,以为只有两个相邻的用户才会产生收费,然后看到题目中输入了一个矩阵就(mengbi)了,赶紧换思路

然后分析了一下收费的规律,发现了一条很重要的性质:
当(n_a < n_b)时,
(2个A->k=2)
(1个A->k=1)
(0个A->k=0)

因此,
在一棵子树中,只有选择两种收费方案中少数的叶节点才会产生贡献,
并且这样的贡献是互不相关的
那么,
对于一个用户,他能否产生贡献取决于他的收费方案以及其祖先节点子树的收费情况
((n_a<n_b)或(n_age n_b))

对于这种贡献计算和叶节点到祖先路径有关的题目,
我们先预处理叶节点,然后在非叶节点上合并(HNOI2018已经吃过亏了)
在这里合并的时候,我们发现祖先收费情况只和(n_a)和(n_b)的有关,
因此我们需要记录人数,然后利用背包合并;

综上所述,我们需要记录子树位置,祖先的收费情况(一个二维向量),人数这三维,使用(f[i][j][k])表示;

在做题的时候,笔者发现了以上的性质,但自己多想认为无法根据父节点的收费情况统计两棵子树的贡献,因此没有做出来,今后看题目还是需要入手一个小样例,让自己更加接近题目的本质

上转移方程;
我们先使用(g[i][j])记录叶节点(i)在自己的第(j)个父亲作为(LCA)的时候和其他节点产生的收费之和;
之后有

[f[i][j][k]=min_{t=0}^{k}{f[ls][j][k-t]+f[rs][j][t]} ]

转移时对于不合法的状态(比如人数不符合子树要求)直接不作转移即可

这里笔者之前又有一个忧虑是转移是(O(2^{4n}))的(其实(O(2^{4n})80)分应该也可以过吧)
那么我们来看时间复杂度到底是多少
我们把这棵树按照深度分层,可以知道其层数不超过(n(nle 10))
而([j][k])这两维在每一层的乘积是一定的,
因为每往下走一层,(j)就会( imes 2)(多一维向量),(k)就会(div 2)(人数少了一半);

因此把([j][k])压作一维,状态总数是(O(2^{2n}))的;
对于计算时的背包转移,每往下一层我们的转移会多一被,但(t)的枚举也少了一半,因此乘积还是(O(2^{2n}))的,共有(n)层,因此这里的时间复杂度是(O(2^{2n}n));

因此总时间复杂度就是(O(2^{2n}+2^{2n}n))。

改了两天半的惨痛教训

code

#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<complex>
#include<vector>
#include<cstdio>
#include<string>
#include<bitset>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define FILE "a"
#define mp make_pair
#define pb push_back
#define RG register
#define il inline
using namespace std;
typedef unsigned long long ull;
typedef vector<int>VI;
typedef long long ll;
typedef double dd;
const dd eps=1e-10;
const int mod=1e9+7;
const int N=3010;
const dd pi=acos(-1);
const int inf=2147483647;
il ll read(){
    RG ll data=0,w=1;RG char ch=getchar();
    while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
    if(ch=='-')w=-1,ch=getchar();
    while(ch<='9'&&ch>='0')data=data*10+ch-48,ch=getchar();
    return data*w;
}

il void file(){
    freopen(FILE".in","r",stdin);
    freopen(FILE".out","w",stdout);
}

int n,w[N],c[N],d[N][N],g[N][N],f[N][N],ans;
#define mid ((l+r)>>1)
void init(int dep,int l,int r){
    if(l==r)return;
    for(RG int i=l;i<=mid;i++)g[dep][i]=d[i][r]-d[i][mid];
    for(RG int i=mid+1;i<=r;i++)g[dep][i]=d[i][mid]-d[i][l-1];
    init(dep+1,l,mid);init(dep+1,mid+1,r);
}
int dfs(int x,int y,int z,int dep){
    if(f[x][(y<<dep)|z]!=-1){
        return f[x][(y<<dep)|z];
    }
    int sum;
    if(dep==n){
        RG int now=x-(1<<n)+1,zz=z;
        sum=c[now]*(w[now]==y);
        for(RG int i=dep-1;~i;i--,zz>>=1)
            if((zz&1)!=y)sum+=g[i][now];
        return f[x][(y<<dep)|z]=sum;
    }
    else{
        sum=inf;int p=(y>=(1<<(n-dep-1)));
        for(RG int i=max(0,y-(1<<(n-dep-1)));i<=min(y,1<<(n-dep-1));i++)
            sum=min(sum,dfs(x<<1,i,z<<1|p,dep+1)+dfs(x<<1|1,y-i,z<<1|p,dep+1));
        return f[x][(y<<dep)|z]=sum;
    }
}

int main()
{
    n=read();
    for(RG int i=1;i<=(1<<n);i++)w[i]=read();
    for(RG int i=1;i<=(1<<n);i++)c[i]=read();
    for(RG int i=1;i<(1<<n);i++)
        for(RG int j=i+1;j<=(1<<n);j++)
            d[i][j]=d[j][i]=read();	
    for(RG int i=1;i<=(1<<n);i++)
        for(RG int j=1;j<=(1<<n);j++)
            d[i][j]+=d[i][j-1];
    init(0,1,(1<<n));ans=inf;memset(f,-1,sizeof(f));
    for(RG int i=0;i<=(1<<n);i++)
        ans=min(ans,dfs(1,i,0,0));
    printf("%d
",ans);
    return 0;
}