定义
树的直径是树上两点间距离的最大值。
树中最远的两个节点之间的距离被称为树的直径,连接这两点的路径被称为树的最长链。
例题
给定一棵树(n<=10000),树中每条边都有一个权值,树中两点之间的距离定义为连接两点的路径边权之和。
求该树任意两点之间的距离最大是多少?
(保证给出的边权为正)
样例输入:
5
2 4 80
3 5 1
1 3 85
2 3 28
样例输出:
193
题意:n个点,n-1条边-----一棵树,求该树的树的直径
法一:BFS|DFS
首先要证明树的直径的一个性质。
从树上任意一个点出发所到达的最远的点一定是树的两个端点之一。
可以用反证法证明: 假设树的直径为(u,v),用(dis(u,v))表示u,v两点间的距离。
假设x出发,距离x最远的距离是y。
先证y在直径外,(x,y)不可能是x出发的最长路径。

设((x,y))交((u,v))于P,那么(dis(x,y)>dis(x,p)+dis(p,v))
又(dis(x,y)=dis(x,p)+dis(p,y))
所以(dis(x,p)+dis(p,y)>dis(x,p)+dis(p,v))
消去(dis(x,p)),同时加上(dis(u,p)), (dis(u,p)+dis(p,y)>dis(u,p)+dis(p,v))
所以(dis(u,y)>dis(u,v))
这显然与((u,v))是树的直径相矛盾,不成立。
另一种情况,假设((x,y))与((u,v))没有交点

在直径上任意取一点p。
那么(dis(x,y)>dis(x,p)+dis(p,v))
又 (dis(x,p)>0),
所以 (2*dis(x,p)>0)
不等式叠加得
(dis(x,y)+2*dis(x,p)>dis(x,p)+dis(p,v))
(dis(x,y)+dis(x,p)>dis(p,v))
(dis(x,y)+dis(x,p)+dis(u,p)>dis(u,p)+dis(p,v))
(dis(u,y)>dis(u,v))
显然这也不成立,所以无论(x,y)与直径有没有交点,只要y在直径外,(x,y)就不可能是x出发的最长路径。
再证y在直径上(且y不是u,v两点时),((x,y))不是x出发的最长路径。
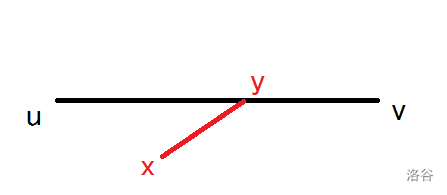
如图,很显然(dis(x,y)<dis(x,y)+dis(y,v))
所以y在直径上(且y不是u,v两点时),((x,y))不是x出发的最长路径。
综上,当且仅当y在直径上且y是u,v两点其中一点时,((x,y))为x出发的最长路径。
所以如何找树的直径呢?
首先以任意一个点为起点,通过dfs或bfs找最长路径,从中选择长度最长的路径到达的点,再次以这个点为起点找最长路径,得到的第二个最长的路径连接的两个点就是树的直径。
很好理解,这里就贴一下代码。
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
#define LL long long
using namespace std;
const int N=10000+5;
const int INF=(-1u)>>1;
int one[N];
int Next[2*N],ver[2*N],edge[2*N];
int tot;
inline void AddEdge(int a,int b,int c)
{
tot++;
Next[tot]=one[a];
one[a]=tot;
ver[tot]=b;
edge[tot]=c;
return;
}
int n;
bool vis[N];
int dis[N];
queue<int> q;
void BFS(int st)
{
memset(vis,0,sizeof vis);
memset(dis,0,sizeof dis);
while(q.size()) q.pop();
int i,j;
int x,y,z;
dis[st]=0;
vis[st]=true;
q.push(st);
do {
x=q.front(); q.pop();
for(i=one[x];i>0;i=Next[i]) {
y=ver[i]; z=edge[i];
if(vis[y])
continue;
dis[y]=dis[x]+z;
vis[y]=true;
q.push(y);
}
} while(q.size());
return;
}
int findmax(int &cmax)
{
cmax=-INF;
int id=0;
for(int i=1;i<=n;i++)
if(dis[i]>cmax) {
cmax=dis[i];
id=i;
}
return id;
}
int ans;
int start,end;
int main()
{
int i,j;
int x,y,z;
scanf("%d",&n);
for(i=1;i<=n-1;i++) {
scanf("%d%d%d",&x,&y,&z);
AddEdge(x,y,z);
AddEdge(y,x,z);
}
BFS(1);
start=findmax(ans);
BFS(start);
end=findmax(ans);
cout<<ans;
return 0;
}
法二:树形Dp
(如果有负权边的话,还是用这种方法吧)。
状态描述:设(f[x])表示从节点x出发走向以x为根的子树,目前为止能够到达的最远节点的距离。
设父节点为u,子节点为v1,v2..
所以 (f[u]=max (f[v1]+edge(u,v1),f[v2]+edge(u,v2),...) ;)
那以u为根子树中两点间经过u的最长距离
加入vn后,ans可能被更新
(ans=max(ans,f[v1]+edge(u,v1)+f[vn]+edge(u,vn),...,f[vn-1]+edge(u,vn-1)+f[vn]+edge(u,vn)))
即 (ans=max(ans,max(f[v1]+edge(u,v1),...,f[vn-1]+edge(u,vn-1))+f[vn]+edge(u,vn)))
所以我们先更新ans,再更新f[u],
那么更新ans时 (f[u]=max(f[v1]+edge(u,v1),...,f[vn-1]+edge(u,vn-1))
所以 (ans=max(ans,f[u]+f[vn]+edge(u,vn)))
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
#define LL long long
using namespace std;
const int N=10000+5;
const int INF=(-1u)>>1;
int one[N];
int Next[2*N],ver[2*N],edge[2*N];
int tot;
inline void AddEdge(int a,int b,int c)
{
tot++;
Next[tot]=one[a];
one[a]=tot;
ver[tot]=b;
edge[tot]=c;
return;
}
int n;
int f[N];
int ans;
void Dp(int u,int fa)
{
int i,j,k,v;
for(i=one[u];i>0;i=Next[i])
if(ver[i]!=fa)
Dp(ver[i],u);
for(i=one[u];i>0;i=Next[i]) {
v=ver[i];
if(v==fa) continue;
ans=max(ans,f[u]+f[v]+edge[i]);
//更新树的直径ans(由当前结点两段之和更新)
f[u]=max(f[u],f[v]+edge[i]);
//更新当前结点所能走的最长路径(保留较长的那边)
//注意顺序!
}
}
int main()
{
int i,j;
int x,y,z;
scanf("%d",&n);
for(i=1;i<=n-1;i++) {
scanf("%d%d%d",&x,&y,&z);
AddEdge(x,y,z);
AddEdge(y,x,z);
}
Dp(1,0);
cout<<ans;
return 0;
}
刚才是一棵树上的任意两点之间的最大距离,那要求以一点为出发点,所能到达的最远距离怎么求呢?
例题
一颗有根树,根节点的编号是1,任意一条边都有权值,对其中的任意一个节点,求离它最远的节点的距离。
输入:第一行n表示有(n(n<=10000))个节点。
后面是(n-1)行,第(i)行三个自然数分别表示:节点编号(x),(y),节点(x)到 (y) 的距离(z(0<=z<=100))
输出(n)行:第(i)行是距离第(i)个节点的最远距离。
题意:树上要求以一点为出发点,所能到达的最远距离。
样例输入:
5
1 2 87
3 5 10
1 3 85
4 2 8
样例输出:
95
182
180
190
190
法一:BFS|DFS
与上一题的法一相同。
上一题的法一已经证明了
树上任意一点出发的最长路径的另一端点一定是树的直径的两个端点之一。
那么,我们先找出树的直径的两个端点,再由两个端点分别BFS|DFS,对两次的dis取大者,即可。
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
#define LL long long
using namespace std;
const int N=10000+5;
const int INF=(-1u)>>1;
int one[N];
int Next[2*N],ver[2*N],edge[2*N];
int tot;
inline void AddEdge(int a,int b,int c)
{
tot++;
Next[tot]=one[a];
one[a]=tot;
ver[tot]=b;
edge[tot]=c;
return;
}
int n;
bool vis[N];
int dis[N];
queue<int> q;
void BFS(int st)
{
memset(vis,0,sizeof vis);
memset(dis,0,sizeof dis);
while(q.size()) q.pop();
int i,j;
int x,y,z;
dis[st]=0;
vis[st]=true;
q.push(st);
do {
x=q.front(); q.pop();
for(i=one[x];i>0;i=Next[i]) {
y=ver[i]; z=edge[i];
if(vis[y])
continue;
dis[y]=dis[x]+z;
vis[y]=true;
q.push(y);
}
} while(q.size());
return;
}
int findmax(int &cmax)
{
cmax=-INF;
int id=0;
for(int i=1;i<=n;i++)
if(dis[i]>cmax) {
cmax=dis[i];
id=i;
}
return id;
}
int ans;
int start,end;
int f[N];
int main()
{
int i,j;
int x,y,z;
scanf("%d",&n);
for(i=1;i<=n-1;i++) {
scanf("%d%d%d",&x,&y,&z);
AddEdge(x,y,z);
AddEdge(y,x,z);
}
BFS(1);
start=findmax(ans);
BFS(start);
for(i=1;i<=n;i++)
f[i]=max(f[i],dis[i]);
end=findmax(ans);
BFS(end);
for(i=1;i<=n;i++)
f[i]=max(f[i],dis[i]);
for(i=1;i<=n;i++)
printf("%d
",f[i]);
return 0;
}
法二:树形Dp(换根法)
求任意节点为起点的最长路径(每条边有权值)
状态描述|约定:
(f[u][0]):u为根子树中,u为起点获得的最长路径(下行)
(f[u][1]):u为根子树中,u为起点获得的次长路径(下行) (规定:最长路径和次长路径不经过同一个子节点);
(f[u][2]):表示u为起点,往上走(父亲方向)可以获得的最长路径(上行)
下行情况:(蓝圈内)

(图片来自网络,侵删)
假设v是u的子节点
(f[u][0]=max(f[u][0],f[v][0]+edge(u,v)))
如果更新了最长,就把原来的最长给次长,并且不更新次长。
如果没更新最长,那么用子节点的最长更新次长。
(f[u][1]=max(f[u][1],f[v][0]+edge(u,v)))
上行情况
(f[u][2]):表示u为起点,往上走(父亲方向)可以获得的最长路径(上行)
那么有两种情况
1、(f[u][2])在绿圈内
2、出了绿圈
“换根法” 用fa求u
(f[u][2])在绿圈内,
那么 (f[u][2])就是fa节点的下行+edge(u,fa);
fa节点的下行(分两种情况,经过u和不经过u),
这时候把下行路径分成次长和最长就起作用了。
如果fa的最长下行路径不经过u,那么 (f[u][2]=max(f[u][2],f[fa][0]+edge(u,fa)))
如果fa的最长下行路径经过u,就取次长,(f[u][2]=max(f[u][2],f[fa][1]+edge(u,fa)))
(f[u][2])出了绿圈
利用最优子结构的性质,把该问题分成两段。
一是u到fa(是个定值),二是fa的上行最大值(子问题)
这就把原问题转化成子问题来求解,
(f[u][2]=max(f[u][2],f[fa][2]+edge(u,fa)))
Code:
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
#define LL long long
using namespace std;
const int N=10000+5;
const int INF=(-1u)>>1;
int one[N];
int Next[2*N],ver[2*N],edge[2*N];
int tot;
inline void AddEdge(int a,int b,int c)
{
tot++;
Next[tot]=one[a];
one[a]=tot;
ver[tot]=b;
edge[tot]=c;
return;
}
int n;
int f[N][3],g[N];
void Dp1(int u,int fa)
{
int i,j,k,v;
for(i=one[u];i>0;i=Next[i])
if(ver[i]!=fa)
Dp1(ver[i],u);
for(i=one[u];i>0;i=Next[i]) {
v=ver[i];
if(v==fa) continue;
if(f[v][0]+edge[i]>f[u][0]) {
f[u][1]=f[u][0]; //把最长推给次长
f[u][0]=f[v][0]+edge[i]; //更新最长
g[u]=v; //记录最长经过的子节点
}
else if(f[v][0]+edge[i]>f[u][1])
f[u][1]=f[v][0]+edge[i]; //没更新成功就更新次长
}
return;
}
void Dp2(int u,int fa)
{
int i,j,k,v;
for(i=one[u];i>0;i=Next[i]) {
v=ver[i];
if(v==fa) continue;
if(g[u]!=v)
f[v][2]=max(f[v][2],f[u][0]+edge[i]);
else f[v][2]=max(f[v][2],f[u][1]+edge[i]);
f[v][2]=max(f[v][2],f[u][2]+edge[i]);
Dp2(v,u);
}
return;
}
int main()
{
int i,j;
int x,y,z;
scanf("%d",&n);
for(i=1;i<=n-1;i++) {
scanf("%d%d%d",&x,&y,&z);
AddEdge(x,y,z);
AddEdge(y,x,z);
}
Dp1(1,0);
Dp2(1,0);
for(i=1;i<=n;i++)
printf("%d
",max(f[i][0],f[i][2]));
return 0;
}
换根法的用处不只是求树的直径。
最后附上用于对拍的数据生成器:
#include<bits/stdc++.h>
#define LL long long
using namespace std;
int n;
const int N=10000+5;
int par[N];
int Find(int x)
{
if(par[x]!=x) return par[x]=Find(par[x]);
return x;
}
void Join(int x,int y)
{
int x_=Find(x);
int y_=Find(y);
if(x_==y_)
return;
par[x_]=y_;
return;
}
int main()
{
srand(time(0));
int i,j;
int x,y,z;
n=10000;
printf("%d
",n);
for(i=1;i<=n;i++)
par[i]=i;
for(i=1;i<=n-1;i++) {
x=rand()%n+1;
y=rand()%n+1;
if(Find(x)==Find(y)) {
i--;
continue;
}
Join(x,y);
z=rand()%100+1;
printf("%d %d %d
",x,y,z);
}
return 0;
}
例题地址
| 1072 | 树的最长路径 |
|---|---|
| 1073 | 树的中心 |