BF、kmp算法

第七周 字符串匹配

BF算法，kmp算法

BF：时间复杂度为 O(m*n)

 

int Index_BF(SString S, SString T, int pos)
{
    int i = pos, j = 1;
    while (i <= S.length &&j <= T.length)
    {
        if (S.ch[i] == T.ch[j])
        {
            ++i;
            ++j;
        }
        else {
            i = i - j + 2;
            j = 1;
        }
    }
        if (j > T.length)
            return i - T.length;
        else
            return 0;
}

模式串和主串均是存放于字符数组中。（这里是从下标为1开始存储，以便后面操作）

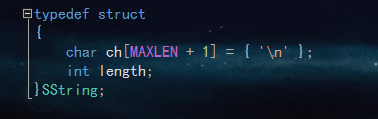
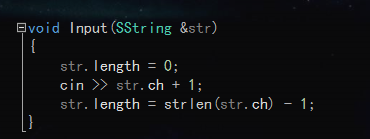
BF比较简单，直接暴力匹配。每次匹配失败，i 回溯到本轮起始位置的下一位。（效率较低）

测试：

结果：

————————————————————————————————————————————————————————————————————

————————————————————————————————————————————————————————————————————

——————————————————————————————————————————————————————————————————-——

KMP:时间复杂度为O(m+n)

因为kmp的思想要写的过程太多（我懒得打字），还有结合字符串图更清晰

所以借鉴：https://www.cnblogs.com/yjiyjige/p/3263858.html

 感觉kmp还是很好理解，老师让我讲一遍却又表达不清楚（自己能懂就是不知道怎么把它完整表达出来）

 主要就是 i不用回溯，设立了next[ ]值，即k值，模式串中失配位对应的k值即为下一轮 j重新开始匹配的位置

至于k值得来历，简单点讲 就是为了模式串与主串匹配时减少BF无意义的比较情况，需要在部分匹配成功的

情况下 一次移动k-1 位来提高效率。假设在S主串中的第i位，T模式串的第j为失配，那么i不动，下一次匹配就从第j位

对应的k值开始（j=k=next [ j ]），即下一次从模式串的第k位开始匹配。

计算k值：从kmp算法中，失配后比较的是S的第 i 位与T的第 k 位，那么T中 k 前面的串（k-1）个字符肯定是和S中

i 的前面(k-1)个字符是匹配的。由匹配成功的部分可以得知：S中的i 前面（k-1）个字符又与T中j 前面的（k-1）个字符

是已经匹配成功的，所以前面两句话就等于:

　　　　　　　　　　　　　　　　 T[1...k-1] = T[ j-(k-1)...j-1]

从上面的式子可以看出模式串与主串的比较 变成了模式串自己前缀和后缀的比较，这样找到模式串前缀与后缀所能匹配的最大

长度就等于我们的k-1，也就找出了k;

int Index_KMP(SString S, SString T, int pos, int next[])
{
    int i = pos, j = 1;
    while (i <= S.length&&j <= T.length)
    {
        if (j == 0 || S.ch[i] == T.ch[j])
        {
            ++i;
            ++j;
        }
        else
            j = next[j];
    }
    if (j > T.length)
        return i - T.length;
    else
        return 0;
}

下面是next[ ]值计算

例子：

 

算法:

 上面的next值在某些情况下仍有点缺陷，所以有了一个修正next算法

修正next算法：

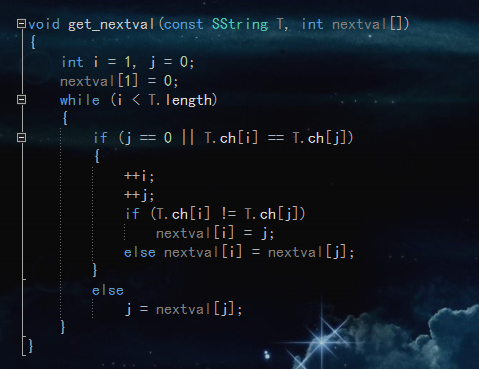
结果：

  

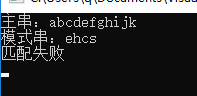
 kmp算法还是挺重要的，理解清楚了还应该记住模板，说不定日后或者OJ用得着呢。