【BZOJ4892】DNA(后缀数组)
题面
题解
看到这道题目,我第一反应是(FFT)???
然后大力码出了一个(FFT)
就像这样
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define ll long long
#define RG register
#define MAX 200000
inline int read()
{
RG int x=0,t=1;RG char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')t=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
return x*t;
}
const double Pi=acos(-1);
struct Complex{double a,b;}A[MAX],B[MAX],W[MAX];
Complex operator+(Complex a,Complex b){return (Complex){a.a+b.a,a.b+b.b};}
Complex operator-(Complex a,Complex b){return (Complex){a.a-b.a,a.b-b.b};}
Complex operator*(Complex a,Complex b){return (Complex){a.a*b.a-a.b*b.b,a.b*b.a+a.a*b.b};}
char C[MAX],S[MAX],dna[4]={'A','G','C','T'};
int n,m,ans[MAX],N,r[MAX],l;
void FFT(Complex *P,int opt)
{
for(int i=1;i<N;++i)if(i<r[i])swap(P[i],P[r[i]]);
for(int i=1;i<N;i<<=1)
for(int p=i<<1,j=0;j<N;j+=p)
for(int k=0;k<i;++k)
{
Complex w=(Complex){W[N/i*k].a,W[N/i*k].b*opt};
Complex X=P[j+k],Y=w*P[i+j+k];
P[j+k]=X+Y;P[i+j+k]=X-Y;
}
if(opt==-1)for(int i=0;i<N;++i)P[i].a/=N;
}
int main()
{
int T=read();
while(T--)
{
scanf("%s",C);scanf("%s",S);l=0;
n=strlen(C);m=strlen(S);reverse(&S[0],&S[m]);
for(N=1;N<n+m;N<<=1)++l;
for(int i=0;i<n;++i)ans[i]=0;
for(int i=0;i<N;++i)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
for(int i=1;i<N;i<<=1)
for(int k=0;k<i;++k)W[N/i*k]=(Complex){cos(k*Pi/i),sin(k*Pi/i)};
for(int p=0;p<4;++p)
{
for(int i=0;i<N;++i)A[i]=B[i]=(Complex){0,0};
for(int i=0;i<n;++i)A[i]=(Complex){C[i]==dna[p]?1.0:0,0};
for(int i=0;i<m;++i)B[i]=(Complex){S[i]==dna[p]?1.0:0,0};
FFT(A,1);FFT(B,1);
for(int i=0;i<N;++i)A[i]=A[i]*B[i];
FFT(A,-1);
for(int i=m-1;i<n;++i)ans[i]+=(int)(A[i].a+0.5);
}
int tot=0;
for(int i=m-1;i<n;++i)if(ans[i]+3>=m)++tot;
printf("%d
",tot);
}
return 0;
}
然后洛谷上交一发
恩。。。(FFT)果然常数名不虚传
那么就用(NTT)吧
就像这样
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define ll long long
#define RG register
#define MAX 200000
inline int read()
{
RG int x=0,t=1;RG char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')t=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
return x*t;
}
const int MOD=998244353;
int A[MAX],B[MAX],W[MAX];
char C[MAX],S[MAX],dna[4]={'A','G','C','T'};
int n,m,ans[MAX],N,r[MAX],l;
int fpow(int a,int b)
{
int s=1;
while(b){if(b&1)s=1ll*s*a%MOD;a=1ll*a*a%MOD;b>>=1;}
return s;
}
void NTT(int *P,int opt)
{
for(int i=1;i<N;++i)if(i>r[i])swap(P[i],P[r[i]]);
for(int i=1;i<N;i<<=1)
{
int w=fpow(3,(MOD-1)/(i<<1));W[0]=1;
for(int j=1;j<i;++j)W[j]=1ll*W[j-1]*w%MOD;
for(int p=i<<1,j=0;j<N;j+=p)
for(int k=0;k<i;++k)
{
int X=P[j+k],Y=P[i+j+k]*1ll*W[k]%MOD;
P[j+k]=(X+Y)%MOD;P[i+j+k]=(X+MOD-Y)%MOD;
}
}
if(opt==-1)
{
reverse(&P[1],&P[N]);
for(int i=0,inv=fpow(N,MOD-2);i<N;++i)P[i]=1ll*P[i]*inv%MOD;
}
}
int main()
{
int T=read();
while(T--)
{
scanf("%s",C);scanf("%s",S);l=0;
n=strlen(C);m=strlen(S);reverse(&S[0],&S[m]);
for(N=1;N<n+m;N<<=1)++l;
for(int i=0;i<n;++i)ans[i]=0;
for(int i=0;i<N;++i)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
for(int p=0;p<4;++p)
{
for(int i=0;i<N;++i)A[i]=B[i]=0;
for(int i=0;i<n;++i)A[i]=C[i]==dna[p];
for(int i=0;i<m;++i)B[i]=S[i]==dna[p];
NTT(A,1);NTT(B,1);
for(int i=0;i<N;++i)A[i]=1ll*A[i]*B[i]%MOD;;
NTT(A,-1);
for(int i=m-1;i<n;++i)ans[i]+=A[i];
}
int tot=0;
for(int i=m-1;i<n;++i)if(ans[i]+3>=m)++tot;
printf("%d
",tot);
}
return 0;
}
这样就很开心了
当然,这个时间在洛谷能够排到多少呢?
倒数第一诶。。。
很舒服啊。
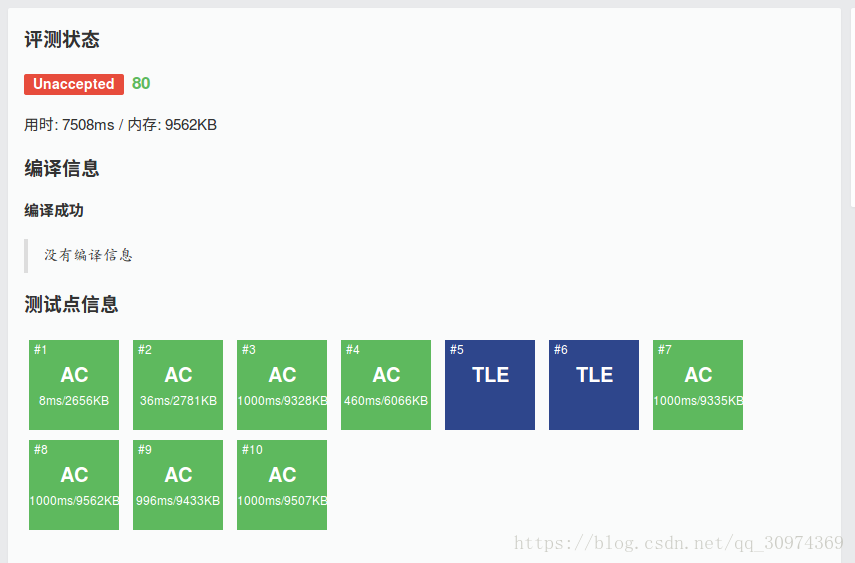
然后就在(BZOJ)上交了一发,然后(TLE)了。
问了一下早就切掉了这道题的(zsy)。
原来这题根本就不是(NNT)啊。。。
我们考虑如何暴力,
求出(SA)之后我们可以做到(O(1))查询(lcp)
然后暴力往后跳就行了,因为不会跳超过三次,
所以直接暴力就行了。。。
时间复杂度(O(Tnlogn))
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define ll long long
#define RG register
#define MAX 222222
inline int read()
{
RG int x=0,t=1;RG char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')t=-1,ch=getchar();
while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();
return x*t;
}
int n,m,N;
int SA[MAX],rk[MAX],hg[20][MAX],lg[MAX],a[MAX],t[MAX],x[MAX],y[MAX];
bool cmp(int i,int j,int k){return y[i]==y[j]&&y[i+k]==y[j+k];}
void GetSA()
{
int m=50;
for(int i=1;i<=m;++i)t[i]=0;
for(int i=1;i<=n;++i)t[x[i]=a[i]]++;
for(int i=1;i<=m;++i)t[i]+=t[i-1];
for(int i=n;i>=1;--i)SA[t[x[i]]--]=i;
for(int k=1;k<=n;k<<=1)
{
int p=0;
for(int i=1;i<=n;++i)y[i]=0;
for(int i=n-k+1;i<=n;++i)y[++p]=i;
for(int i=1;i<=n;++i)if(SA[i]>k)y[++p]=SA[i]-k;
for(int i=0;i<=m;++i)t[i]=0;
for(int i=1;i<=n;++i)t[x[y[i]]]++;
for(int i=1;i<=m;++i)t[i]+=t[i-1];
for(int i=n;i>=1;--i)SA[t[x[y[i]]]--]=y[i];
swap(x,y);
x[SA[1]]=p=1;
for(int i=2;i<=n;++i)x[SA[i]]=cmp(SA[i],SA[i-1],k)?p:++p;
if(p>=n)break;
m=p;
}
for(int i=1;i<=n;++i)rk[SA[i]]=i;
for(int i=1,j=0;i<=n;++i)
{
if(j)--j;
while(a[i+j]==a[SA[rk[i]-1]+j])++j;
hg[0][rk[i]]=j;
}
for(int j=1;j<=lg[n];++j)
for(int i=1;i+(1<<j)-1<=n;++i)
hg[j][i]=min(hg[j-1][i],hg[j-1][i+(1<<(j-1))]);
}
int lcp(int i,int j)
{
i=rk[i];j=rk[j];if(i>j)swap(i,j);
if(i==j)return 1e9;++i;
int l=lg[j-i+1];
return min(hg[l][i],hg[l][j-(1<<l)+1]);
}
char S0[MAX],S[MAX];
int main()
{
int T=read();
for(int i=2;i<MAX;++i)lg[i]=lg[i>>1]+1;
while(T--)
{
scanf("%s",S0+1);scanf("%s",S+1);
n=strlen(S0+1);m=strlen(S+1);
int N=n;
for(int i=1;i<=n;++i)a[i]=S0[i]-64;
a[++n]=27;
for(int i=1;i<=m;++i)a[++n]=S[i]-64;
GetSA();int ans=0;
for(int i=1;i<=N-m+1;++i)
{
int tt=0;
for(int j=1;j<=m&&tt<=3;)
{
if(a[i+j-1]!=a[N+1+j])++tt,++j;
else j+=lcp(i+j-1,N+1+j);
}
ans+=tt<=3;
}
printf("%d
",ans);
}
return 0;
}