题目链接:https://leetcode-cn.com/problems/interleaving-string/description/
参考链接:https://blog.csdn.net/u011095253/article/details/9248073
https://www.cnblogs.com/springfor/p/3896159.html
首先看到字符串的题目: “When you see string problem that is about subsequence or matching, dynamic programming method should come to your mind naturally. ”如果是子字符串和字符串匹配应该想到动态规划。

dp[i][j]表示s1取前i位,s2取前j位,是否能组成s3的前i+j位。
比如:s1="aabcc" s2="dbbca" s3="aadbbcbcac"
dp的数组如上图所示。
dp[0][0]=1;
dp[0][1]:使用s1的第一个字符'1'可以组成s3的第一个字符。然后第二也是如此;aab!=aad。后面的也是一样。
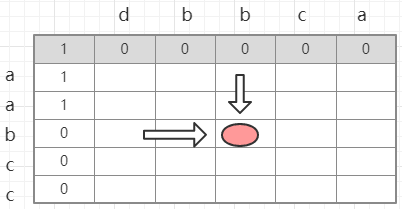
对于dp[i][i]的状态显然是由两个方向的状态来决定的。dp[i][i]是由dp[i-1][j]和dp[i][j-1]来决定的。
public boolean isInterleave(String s1, String s2, String s3) { if (s1 == null || s2 == null || s3 == null) return false; if (s1.length() + s2.length() != s3.length()) return false; int dp[][]=new int[s1.length() + 1][s2.length() + 1]; dp[0][0]=1; for (int i = 1; i < dp.length; i++) { if (s1.charAt(i-1)==s3.charAt(i-1)&&dp[i-1][0]==1) { dp[i][0]=1; } } for (int i = 1; i < dp[0].length; i++) { if (s2.charAt(i-1)==s3.charAt(i-1)&&dp[0][i-1]==1) { dp[0][i]=1; } } for (int i = 1; i < dp.length; i++) { for (int j = 1; j < dp[0].length; j++) { if (s1.charAt(i - 1) == s3.charAt(i + j - 1) && dp[i - 1][j]==1) { dp[i][j] = 1; } if (s2.charAt(j - 1) == s3.charAt(i + j - 1) && dp[i][j - 1]==1) { dp[i][j] = 1; } } } return dp[dp.length-1][dp[0].length-1]==1; }