参考《挑战程序设计》
https://blog.csdn.net/codeswarrior/article/details/80228454
https://blog.csdn.net/sky_zdk/article/details/60320721
集合与二进制
在程序中表示集合的方法有很多种,当元素数比较少时(集合元素的个数不超过32位时可以用int,不超过64时可以用long long),像这样用二进制码来表示比较方便。集合{0,1,2…n-1}的子集可以用以下方式编码成整数。 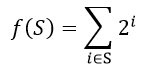
举一个比较直观的例子:
比如一个集合(5,8,3,6,78,45,33,22),我们可以用一个n位的2进制数表示这个集合。
比如11111111代表这个全集,而10100000代表(5,3)这个子集(二进制中1代表这个子集中有全集中相应位置的数字)
像这样表示后,一些集合运算可以对应地写成如下方式:(全集按6个元素)
空集......................................................................0
只含有第i个元素的集合{i}.....................................1<<i (1<<2=4(10进制)=000100(2进制),1<<4=010000)
只含有全部n个元素的集合{0,1,2,....n-1}...............(1<<n)-1 (1<<6=1000000 1<<6-1=0111111)
判断第i个元素是否属于集合S...............................if(S>>i&1)
向集合中加入第i个元素SU{i}................................S|1<<i
从集合中去除第i个元素S{i}..................................S&~(1<<i)
集合S和T的并集....................................................S|T
集合S和T的交集....................................................S&T
将集合{0,1,2,....n-1}所有子集枚举出来,按照这个顺序进行循环的话,S便会从空集开始循环,然后按照{0}、{1}、{0,1}、…、{0,1,…,n-1}的升序枚举出来。
for(s=0;s<1<<n;s++)
{//接下来的操作。
}
枚举某个集合(这个集合本身是别人的子集 比如0111000)的子集。这里sup 是一个二进制码,其本身也是某个集合的子集。例如给定了01101101 这样的集合,要将01100000 或者00101101 等子集枚举出来。前面是从0 开始不断加1 来枚举出了全部的子集。此时,sub+1 并不一定是sup 的子集。而(sub+1)&sup 虽然是sup 的子集,可是很有可能依旧是sub,没有任何改变。所以我们要反过来,从sup 开始每次减1 直到0 为止。由于sub-1 并不一定是sup 的子集,所以我们把它与sup 进行按位与&。这样的话就可以将sup 所有的子集按照降序列举出来。(sub-1)&sup 会忽略sup 中的0 而从sub 中减去1。
int sub = sup;
do {
// 对子集处理
// print_subset(n,sub);
sub = (sub-1) & sup;
} while(sub != sup); // 处理完之后 会有 -1&sup = sup
枚举{0,1,2....n-1}所包含的所有大小为k的子集
int comb = (1<<k)-1;
while (comb< 1<<n)
{
// print_subset(n,comb);
//这里进行针对组合的处理
int x=comb&(-comb), y=comb+x;
comb=((comb&~y)/x>>1)|y;
}
按照字典序的话,最小的子集是(1<< k)-1,所以用它作为初始值。现在我们求出comb其后的二进制码。例如0101110之后的是0110011,0111110之后的是1001111。下面是求出comb下一个二进制码的方法。
(1)求出最低位的1开始的连续的1的区间。
(0101110 -> 0001110)
(2)将这一区间全部变为0,并将区间左侧的那个0变为1。
(0101110 -> 0110000)
(3)将第一步里取出的区间右移,直到剩下的1的个数减少了一个。
(0001110 -> 0000011)
(4)将第二步和第三步中的结果按位取或(0110000|0000011 = 0110011)
对于非零的整数, x&(-x)的值就是将其最低位的1独立出来后的值,这部部分内容在树状数组部分有详细讲解,这里就不赘述了。
将最低位的1取出后,设它为x。那么通过计算y = comb + x,就将comb从最低位的1开始的连续的1都置零了。我们来比较一下~y和comb。在comb中加上x后没有变化的位,在~y中全都取相反的值。而最低位1开始的连续区间在~y中依然是1,区间左侧的那个0在~y中依然也是0.于是通过计算z = comb & ~y 就得到了最低位1开始的连续区间。比如:如果comb = 0101110,则 x = 0000010,y = 0110000,z = 0001110.
同时,y也恰好是第二步要求的值。那么首先将z不断右移,直到最低位为1,这通过计算z/x即可完成。这样再将z/x右移1位,就得到了第三步要求的值。这样我们就求得了comb之后的下一个二进制列。因为是从n个元素的集合中进行选择,所以comb的值不能大于等于
1*2^n,如此一来,就完成了大小为k的所有子集的枚举。
代码如下:
#include<cstdio>
#include<iostream>
using namespace std;
int a[10];
//打印集合元素
void print_subset(int n,int b) //n位的集合,b状态打印
{
printf("{ ");
for (int i=0;i<n;i++)
if (b&(1<<i)) printf("%d ",a[i]);
printf("}
");
}
void p_s(int n)
{
for (int i=0;i<(1<<n);i++) print_subset(n,i); //枚举所有状态
}
int main()
{
int n;
scanf("%d",&n);
//枚举该集合的所有子集
for (int i=0;i<n;i++) a[i]=i;
p_s(n);
//只含有第i个元素的集合{i}
print_subset(n,1<<2);
//含有n个元素的集合
print_subset(n,(1<<n)-1);
//从集合中去除第i个元素S{i}
print_subset(n,((1<<n)-1)&~(1<<1));
//求两个集合的交集
print_subset(n,1<<1|1<<2);
cout<<"子集的子集:" <<endl;
int sup=(1<<n)-3;
int sub = sup;
do {
// 对子集处理
print_subset(n,sub);
sub = (sub-1) & sup;
} while(sub != sup); // 处理完之后 会有 -1&sup = sup
cout<<"大小为k的大小:" <<endl;
int comb = (1<<3)-1;
while (comb< 1<<n)
{
print_subset(n,comb);
//这里进行针对组合的处理
int x=comb&(-comb), y=comb+x;
comb=((comb&~y)/x>>1)|y;
}
return 0;
}
如果一个元素只有两种状态,枚举所有状态的代码如下。
#include<iostream>
#include<string.h>
using namespace std;
//flip第一行可以枚举所有状态
/*
i:0 0 0 0 0
i:1 1 0 0 0
i:2 0 1 0 0
i:3 1 1 0 0
i:4 0 0 1 0
i:5 1 0 1 0
i:6 0 1 1 0
i:7 1 1 1 0
i:8 0 0 0 1
i:9 1 0 0 1
i:10 0 1 0 1
i:11 1 1 0 1
i:12 0 0 1 1
i:13 1 0 1 1
i:14 0 1 1 1
i:15 1 1 1 1
*/
int main(){
int flip[4][4];
int N=4;
for(int i=0; i<1<<N; i++)//1<<N: 2^n
{
cout<<"i:"<<i<<" ";
memset(flip,0,sizeof(flip));
for(int j=0; j<N; j++)
{
flip[0][N-j-1]=i>>j&1;
}
for(int j=0; j<N; j++) {
cout<<flip[0][N-j-1]<<" ";
}
cout<<endl;
}
return 0;
}