机器学习吴恩达-线性回归笔记（1）

回归问题的思想（1）先找到损失函数，（2）求损失函数最小化后的参数

假设我们的数据是（m,n）有m行数据，n个特征（feature）

则我们预测函数为 :

写成向量形式为（xo=1）:

ps:因为存在截距项，这里的X矩阵是n+1维的

定义代价函数CostFunction:

求  minJ(θ)

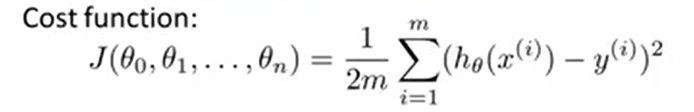
得到目标函数后，我们目标是想要代价函数尽可能小，利用凸优化知识，对J(θ)求偏导并带入梯度下降公式中：

梯度下降请参考：https://www.cnblogs.com/pinard/p/5970503.html

向量式：i=(1,2，...n)

 

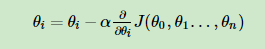
α是步长，决定更新快慢(过大可能会导致溢出)

到这里就能求出所需要的参数的更新公式。

下面的例子是单变量的例子，用的梯度下降方法，因为可以直接画图出，比较直观。

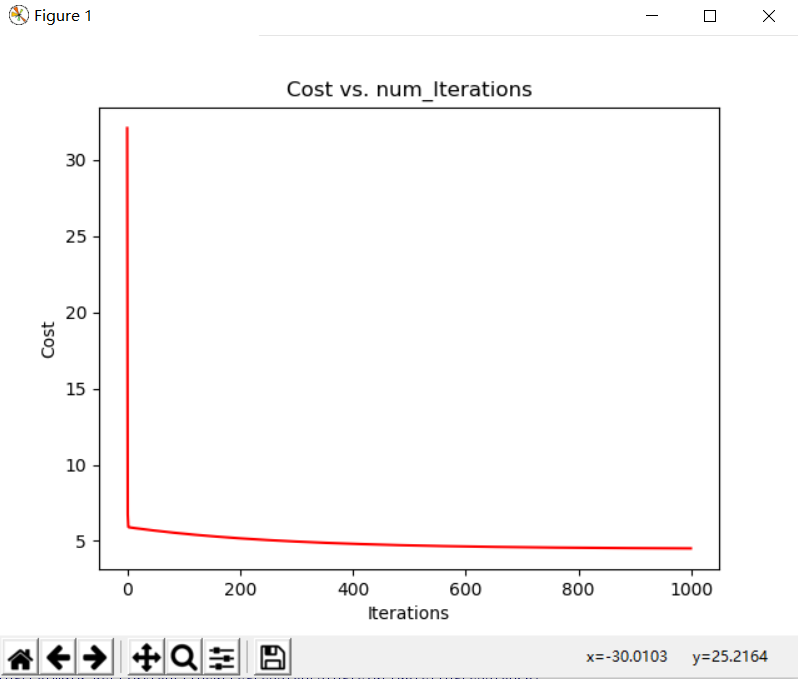
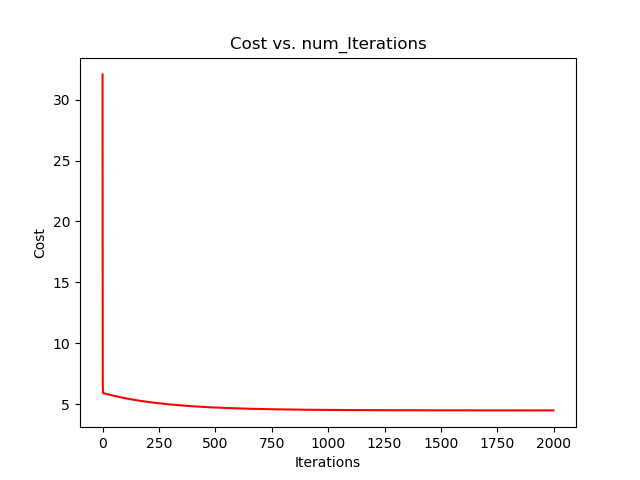
import pandas as pd
import numpy as np
def CostFunction(x,y,theta):
    med_var=np.power((x*theta)-y,2)
    return np.sum(med_var)/(2*len(x))

def Grandent(x,y,theta,alphl,maxcircle):
    m = x.shape[0]
    print('m=',m)
    print('theta shape',theta.shape)
    temp = np.matrix(np.zeros(theta.shape))
    print('temp shape',temp.shape)
    cost = np.zeros(maxcircle)  # 初始化一个ndarray，包含每次迭代的cost
    for k in range(maxcircle):
        # print(theta)
        temp=theta-(alphl/m)*(x.T)*(x*theta-y)
        cost[k]=CostFunction(x,y,theta)
        theta=temp
    return theta,cost


data=pd.read_csv('ex1data1.txt',names=['feature','price'])   #(97, 2)
data.insert(0,'x0',1)
X_dataframe=data.drop(['price'],axis=1)
y_dataframe=data.price
X=np.matrix(X_dataframe.values)  #专程矩阵格式
y=np.matrix(y_dataframe.values)
y=y.T
m,n=X_dataframe.shape
theta=np.zeros((n,1))
alphl=0.01  #开始设置为0.1,会一直报溢出，导致梯度下降方法不收敛
maxcircle=1000

theta_fin,cost=Grandent(X,y,theta,alphl,maxcircle)

import matplotlib.pyplot as plt

fig,ax = plt.subplots()

ax.plot(np.arange(maxcircle), cost, 'red')  # np.arange()返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Cost vs. num_Iterations')

#np.linspace()在指定的间隔内返回均匀间隔的数字
x = np.linspace(data.feature.min(), data.feature.max(), 100) # 横坐标
f = theta_fin[0,0] + (theta_fin[1,0] * x)  # 纵坐标
fig,ax = plt.subplots()
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data['feature'], data.price, label='Traning Data')
ax.legend(loc=2)  # 2表示在左上角
ax.set_xlabel('feature')
ax.set_ylabel('price')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

下面是迭代1000，2000次的结果