2015 Multi-University Training Contest 7 1007(DP)

Gray code

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 208    Accepted Submission(s): 117

Problem Description

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



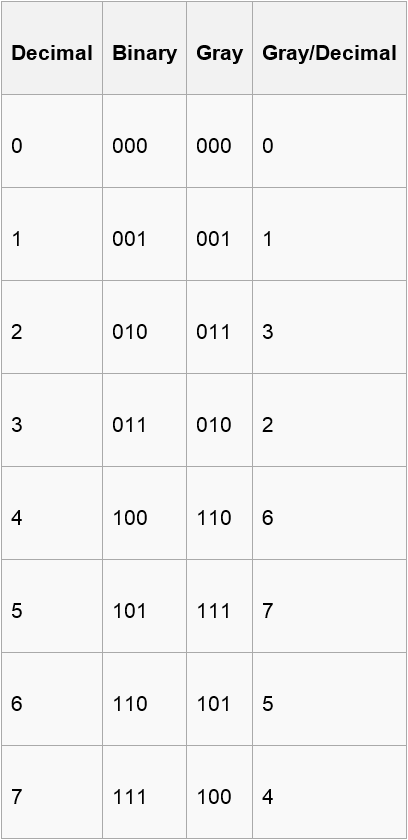
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

 

Input

The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

 

Output

For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most

 

Sample Input

2

00?0

1 2 4 8

????

1 2 4 8

 

Sample Output

Case #1: 12

Case #2: 15

Hint

https://en.wikipedia.org/wiki/Gray_code

http://baike.baidu.com/view/358724.htm

 

 

 

Source

2015 Multi-University Training Contest 7

 

题意：给出一串由 '0'  '1'   '?' 组成的二进制字符串，其中'?'表示可能是0也可能是1，将这个二进制穿换成格雷码，然后在格雷码相应下标有一个权值，为1则加上该权值，为0表示不加，问由二进制转换成格雷码之后权值相加最大值是多少？

分析：

用dp做这道题

dp[i][0]表示二进制下标在下标为 i 处取0转换成格雷码后的权值

dp[i][1]表示二进制下标在下标为 i 处取0转换成格雷码后的权值

 

那么再分情况讨论，由于二进制转换成格雷码的一种方法是

从最右边一位起，依次将每一位与左边一位异或(XOR)，作为对应格雷码该位的值，最左边一位不变(相当于左边是0)

 

再分情况讨论相邻两位的关系

 

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<string>
#include<iostream>
#include<cstring>
#include<cmath>
#include<stack>
#include<queue>
#include<vector>
#include<map>
#include<stdlib.h>
#include<algorithm>
#define LL __int64
using namespace std;
const int MAXN=200000+5;
int dp[MAXN][2],a[MAXN];
char str[MAXN];
int kase,len;
int main()
{
    //freopen("in.txt","r",stdin);
    int Case=0;
    scanf("%d",&kase);
    while(kase--)
    {
        memset(str,0,sizeof(str));
        memset(a,0,sizeof(a));
        memset(dp,0,sizeof(dp));

        scanf("%s",str);
        len=strlen(str);
        for(int i=0;i<len;i++) scanf("%d",&a[i]);

        dp[0][0]=0;
        dp[0][1]=a[0];
        for(int i=1;i<len;i++)
        {
            if(str[i]=='?')
            {
                if(str[i-1]=='?')
                {
                    dp[i][0]=max(dp[i-1][0],dp[i-1][1]+a[i]);//假设当前位为0，前一位为0则转换后还是0，前一位为1则转换后为1
                    dp[i][1]=max(dp[i-1][0]+a[i],dp[i-1][1]);
                }
                else
                {
                    dp[i][0]=dp[i-1][str[i-1]-'0']+a[i]*(0^(str[i-1]-'0'));
                    dp[i][1]=dp[i-1][str[i-1]-'0']+a[i]*(1^(str[i-1]-'0'));
                }
            }
            else
            {
                if(str[i-1]=='?')
                    dp[i][str[i]-'0']=max(dp[i-1][0]+a[i]*(0^(str[i]-'0')),dp[i-1][1]+a[i]*(1^(str[i]-'0')));
                else
                    dp[i][str[i]-'0']=dp[i-1][str[i-1]-'0']+a[i]*((str[i-1]-'0')^(str[i]-'0'));//注意运算符的优先级
            }
        }
        printf("Case #%d: ",++Case);
        if(str[len-1]=='?') printf("%d
",max(dp[len-1][0],dp[len-1][1]));
        else printf("%d
",dp[len-1][str[len-1]-'0']);
    }
    return 0;
}