树状数组例题-数星星，简单题easy，校门外的树2，清点人数

【例1】数星星

天空中有一些星星，这些星星都在不同的位置，每个星星都有个坐标，如果一个星星的左下方（包括正左和正下）有k颗星星，就说这颗星星是k级的。

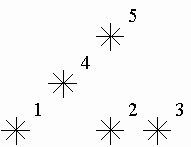
比如，上图中，星星5是3级的（1，2，4在其左下方）

2，4是1级的。

给定星星的位置，输出各级星星的数目。

简述：先按y坐标来排序，就用x来作为参考用树状数组来求解答案（前缀和）

代码

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=20005;
const int MAXX=40005;
struct node{
    int x,y;
}p[MAXN];
int n,m=MAXX,c[MAXX],ans[MAXX];
int lowbit(int x){
    return x&(-x);
}
void update(int x,int y){
    while(x<=m)c[x]+=y,x+=lowbit(x);
}
int sum(int x){
    int tot=0;
    while(x){
        tot+=c[x];
        x-=lowbit(x);
    }
    return tot;
}
int main(){
    cin>>n;
    for(int i=1;i<=n;++i)cin>>p[i].x>>p[i].y;
    for(int i=1;i<=n;++i){
        int u=p[i].x+1;
        int v=sum(u);
        update(u,1);
        ans[v]++;
    }
    for(int i=0;i<n;++i)cout<<ans[i]<<endl;
}

【例2】校门外的树2

校门外有很多树，有苹果树，香蕉树，有会扔石头的，有可以吃掉补充体力的……如今学校决定在某个时刻在某一段种上一种树，保证任一时刻不会出现两段相同种类的树，现有两个操作：K=1，K=1，读入l、r表示在区间[l,r]中种上一种树，每次操作种的树的种类都不同K=2，读入l,r表示询问l~r之间能见到多少种树（l,r>0）

简述：这题不能用暴力的方法。所以我们将线段看成括号序列（即左右打上标记，由此就是范围内有一种树），再用前缀和求解。

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=2000005;
int n,c_1[MAXN],m,c_2[MAXN];
inline int lowbit(int x){
    return x&(-x);
}
void update_1(int x,int y){
    for(;x<=n;x+=lowbit(x))c_1[x]+=y;
}
void update_2(int x,int y){
    for(;x<=n;x+=lowbit(x))c_2[x]+=y;
}
int sum_1(int x){
    int res=0;
    for(;x;x-=lowbit(x))res+=c_1[x];
    return res;
}
int sum_2(int x){
    int res=0;
    for(;x;x-=lowbit(x))res+=c_2[x];
    return res;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;++i){
        int k,l,r;
        cin>>k>>l>>r;
        if(k==1)update_1(l,1),update_2(r,1);
        else printf("%d
",sum_1(r)-sum_2(l-1));
    }
}

【例3】清点人数

初始时，火车上没有学生；当同学们开始上火车时，年级主任从第一节车厢出发走到最后一节车厢，每节车厢随时都有可能有同学上下。年级主任走到第m节车厢时，他想知道第１到m这m节车厢上一共有多少学生，但是他没有调头往回走的习惯．也就是说每次当他提问时，m总会比前一次大。

第一行两个整数n,k，表示火车共有n节车厢以及k个事件。接下来有k行，按时间先后给出k个事件，每行开头都有一个字母A,B或C，如果字母为A，接下来是一个数m，表示年级主任现在在第m节车厢；如果为B，接下来两个数m,p，表示在第m节车厢有p名学生上车；如果为C，接下来两个数m,p，表示在第m节车厢有p名学生下车。学生总人数不会超过100000。

简述：板子题，树状数组求解。

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=2000005;
int n,c[MAXN],m;
inline int lowbit(int x){
    return x&(-x);
}
void update(int x,int y){
    for(;x<=n;x+=lowbit(x))c[x]+=y;
}
int sum(int x){
    int res=0;
    for(;x;x-=lowbit(x))res+=c[x];
    return res;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;++i){
        int a,b;
        char k[2];
        scanf("%s %d",k,&a);
        if(k[0]=='A')cout<<sum(a)<<endl;
        else if(k[0]=='B'){
            scanf("%d",&b);
            update(a,b);
        }
        else{
            scanf("%d",&b);
            update(a,-b);
        }
    }
}

【例4】简单题easy

有一个n个元素的数组，每个元素初始均为0。有m条指令，要么让其中一段连续序列数字反转——0变1，1变0（操作1），要么询问某个元素的值（操作2）。

第一行包含两个整数n，m，表示数组的长度和指令的条数，以下m行，每行的第一个数t表示操作的种类。若t=1，则接下来有两个数L, R (L<=R)，表示区间[L, R]的每个数均反转；若t=2，则接下来只有一个数I，表示询问的下标。

简述：跟校门外的树差不多，都是用双端打标记。这次标记的是区间内修改次数，修改奇数次答案为1，偶数次为0

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=2000005;
int n,c_1[MAXN],m,c_2[MAXN];
inline int lowbit(int x){
    return x&(-x);
}
void update_1(int x,int y){
    for(;x<=n;x+=lowbit(x))c_1[x]+=y;
}
void update_2(int x,int y){
    for(;x<=n;x+=lowbit(x))c_2[x]+=y;
}
int sum_1(int x){
    int res=0;
    for(;x;x-=lowbit(x))res+=c_1[x];
    return res;
}
int sum_2(int x){
    int res=0;
    for(;x;x-=lowbit(x))res+=c_2[x];
    return res;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;++i){
        int k,l,r;
        cin>>k>>l;
        if(k==1){
            cin>>r;
            update_1(l,1),update_2(r,1);
        }
        else{
            int u=sum_1(l)-sum_2(l-1);
            printf("%d
",u%2);
        }
    }
}