--------马丹、刘丽萍 基于不同频率协方差矩阵的等风险比例投资组合-----------
- 已实现协方差矩阵RCOV
1.令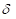 表示交易日内的取样间隔,则每日样本量
表示交易日内的取样间隔,则每日样本量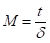 ,当资产价格服从连续路径的
,当资产价格服从连续路径的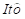 过程时,实现协方差时组合协方差矩阵的一致估计,其基本形式为;
过程时,实现协方差时组合协方差矩阵的一致估计,其基本形式为;
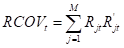
其中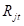 是第t日第j个交易时刻的收益向量。已有研究大多采用RCOV估计高频协方差矩阵,并用其计算组合权数。但是在市场微观结构噪声的影响下,RCOV不再是协方差矩阵的无偏一致估计量,尤其是在采样频率非常高的时候,RCOV更主要的估计了噪声的协方差。且交易频率越高,RCOV中的噪声成分越大。
是第t日第j个交易时刻的收益向量。已有研究大多采用RCOV估计高频协方差矩阵,并用其计算组合权数。但是在市场微观结构噪声的影响下,RCOV不再是协方差矩阵的无偏一致估计量,尤其是在采样频率非常高的时候,RCOV更主要的估计了噪声的协方差。且交易频率越高,RCOV中的噪声成分越大。
- 多元核光滑协方差估计KCOV
为消除围观结构噪声的影响,Barndorff-Nielsen等提出KCOV,通过在局部窗宽对协方差进行核光滑,减少了微观结构噪声的影响,得到协方差矩阵的一致估计。通常KCOV小于RCOV。
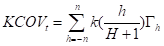
其中,k为核函数。是第h个子区间中协方差矩阵的距估计量。
-------------多维金融高频协方差阵预测模型的比较分析,刘丽萍-----------
一、两种保证预测协方差阵正定性的方法
- Chiriac 和Voev(2011)提出对已实现协方差阵的乔列斯基分解因素进行建模,在没有参数限制的情况下,保证了预测结果的正定性。Chiriac 和Voev认为,观察到的协方差自相关的长记忆性,被保存在乔列斯基因素的自相关中。
- Bauer和Vorkink(2011)提出的对已实现协方差进行对数化变换来保证预测协方差阵的正定性。
二、为了捕捉长记忆性,该文采用两种方法对高频协方差矩阵进行预测。
1.Chiriac 和Voev提出的VARFIMA模型:基于矩阵的乔列斯基分解的基础上建立,捕捉长记忆性 的同时保证正定性。但是使用VARFIMA模型时,当预测的协方差阵的维度较高时,由于待估的参数较多,为 (n为资产个数)
(n为资产个数)
应用来较为困难,存在维数灾难问题。CF-ARMA(2,1)模型克服了该缺点。
- 对乔列斯基分解因素分别建立ARMA(2,1)模型,来取代VARFIMA模型
2.FI-VAR模型:采用分别整合的向量自回归FIVAR模型来代替VARFIMA模型,时的参数的估计问题得到简化
三、多元异质自回归MHAR模型
异质市场假说:不同的参与者对市场的预期时不同的,他们在风险偏好、信息获取等方面存在着不同,即市场上存在异质的交易者。一般来说,处于不同持有期的交易者对未来的预期往往是不同的,因而对波动也会产生不同的影响。异质自回归已实现波动HAR-RV模型是一种多成分波动模型,通过一个自回归结构来对每日、每周、每月的波动成分进行加总,来捕捉已实现波动的异质性。
- 基于乔列斯基分解的CF-HAR模型
- 基于矩阵的对数变换的LOG-HAR模型
四、结论
基于矩阵的对数化变换的多元异质自回归模型LOG-HAR模型在所有的损失函数下都是预测能力最好的预测模型,并且基于高频数据的协方差阵预测模型的预测效果要优于基于低频数据的协方差阵预测模型。
-------基于市场微观结构噪声和跳跃的金融高频协方差阵的估计,刘丽萍,2014--------------
一、提出背景
基于高频数据的协方差阵估计挖掘了数据中更丰富的信息,使得协方差阵的估计更加准确。但是,市场微观结构噪声的影响也越来越明显,已实现协方差阵RCOV的估计结果不再准确。一些学者提出剔除了跳跃影响的高频协方差阵估计方法,但当时有的要么是只考虑了市场微观结构噪声,要么只是考虑了跳跃的影响,很少又文献同时考虑噪声和跳跃对高频协方差阵估计的影响。该文提出修正的门限预平均已实现协方差阵MTPRCOV,该估计量将预平均方法和门限的思想结合起来。其中国预平均方法用来处理市场微观结构噪声的 影响,门限用来剔除跳跃的影响。MTPCOV实际上是马丹,尹优平(2012)提出的已实现波动MTPRV的多元扩展。
二、MTPCOV(修正的门限预平均已实现协方差阵)的构造
MTPCOV的主对角线是各个资产的MTPRV,副对角线元素是两两资产之间的修正的门限预平均已实现协方差MTPCV(修正的门限预平均已实现协方差),
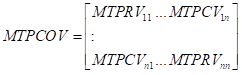
马丹,尹优平(2012)已经证明MTPRV 是积分波动IV的一致估计量,若MTPCV是积分协方差ICV的一直估计量,则MTPCV 便是积分协方差阵ICOV的一致估计量,即:
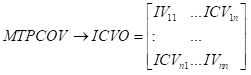
三、模拟
1.选择合适的窗宽:用数值方法,首先对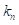 设定一个合理的取值区间,然后在设定的范围内进行不断搜索来寻找最优的窗宽。
设定一个合理的取值区间,然后在设定的范围内进行不断搜索来寻找最优的窗宽。
判断方法:平方误差MSE是估计值和真实值之间误差平方的期望,考虑采用该统计量来预测估计值与真实值之间的差异。每一个窗宽都会对应一个MTPCV的值,且MTPCV是积分协方差的一致估计量,所以可计算出每一个MTPCV估计值与积分协方差ICV之间的平均平方误差MSE,找出其中最小的MSE值,所对应的窗宽就是最有的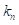 。
。
2.选取合适的门限函数:该问选择Christensen,Oomen和Podolskij(2010)提出的门限函数。
3.将本文提出的MTPCV估计量与MPCV已实现双幂次协方差BPCV估计量进行对比。
四、数据实验
1.为了比较不同样本容量对高频数据协方差的影响,分别模拟抽样间隔为1分钟,30秒,5秒以及1秒的数据。分别模拟1000次。
五、结论:无论评价标准是MSE还是MAE,无论样本容量是多少,修正的门限预平均已实现协方差MTPCV的估计效果都是最好的。MTPCV估计量能够有效的将市场微观结构噪声和跳跃从协方差元素的估计中分离出来,计算出跳跃和市场微观结构噪声对协方差估计量产生的影响,并且,在估计不同资产间的MTPCV时,窗宽的选择对样本容量并不敏感,又因为MTPRV估计量对窗宽的选择也不敏感,因此由他们构造的MTPCOV能够很好的应用在投资组合中。
---------基于因子分析法的金融高频已实现波动的预测,刘丽萍,2017-----------
一、提出背景
Corsi(2004)提出异质自回归已实现波动HAR-RV模型,通过自回归结构来对每日、每周、每月的波动成分进行加总,以此来捕捉已实现波动的异质性。Andersen等(2007)对HAR-RV模型进行了扩展,考虑了跳跃对于波动的影响,将已实现波动分解为连续样本路径方差和离散跳跃方差,以此构建了HAR-RV-CJ模型。但是当考虑的资产数目较多时,若仍采用这两种模型将会非常复杂,不易于实现。作者在因子分析法的基础上,提出了剔除了跳跃影响的波动预测模型——F-RV-J模型。
二、模型
1.用门限函数检验跳跃是否存在
2.首先确定因子的数目,本文作者采用Bai和Ng的的参数方法来去确定因子的数目;然后对因子载荷矩阵进行估计。作者采用的是渐进主成分分析方法来估计大量数据的公共因子,该方法非常适用于高维的已实现波动估计量,因为此时不再存在维数诅咒的问题。
3.作者采用Hirose等(2012)提出的基于非凸惩罚似然方法的稀疏估计量来估计因子模型F-RV-J。该方法克服了传统两步估计法的缺点,引入惩罚似然方法对因子载荷矩阵施加非凸性惩罚,可以产生更好的稀疏解决方案。
三、实证
1.将本模型与经典的HAR-RV-J模型进行比较分析
2.比较标准:损失函数RMSE,MAE;MCS检验以及对于在险价值VAR的预测能力
四、结论
比较发现F-RV-J模型无论是在预测精读还是对风险的预测能力方面,都优于其他的波动预测模型。另一方面使得波动的预测更容易实现,尤其是当考虑的资产的维度较高时,该模型的预测效果更好,他克服了维数诅咒的问题。
-----------------考虑高频数据影响的BEKK模型的估计及其应用---------------------
一、背景
多元GARCH模型时传统的多元协方差阵的估计和预测模型,常见的包括:CCC-GARCH模型(Bollerslev,1990),BEKK模型(Engle和Korner,1995;Ding和Engle,2001),DCC模型(Engle,2002).传统的多元GARCH模型时基于低频数据的协方差阵的估计,但不适用于高频数据。本文作者考虑将高频数据的协方差阵的估计方法应用到BEKK模型的估计中,分别将已实现波动RCOV和双频已实现波动TSCOV应用到BEKK模型中,提出BEKK-RCOV和BEKK-TSCOV模型,将高频数据引入到协方差阵估计过程中的同时,还可以对协方差阵直接进行预测,提高了协方差阵的估计效率。
二、模型构建
1.RCOV的形式为: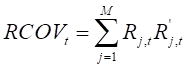 ,
,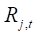 是N*1向量,表示第t日内第j个交易时刻的收益率。
是N*1向量,表示第t日内第j个交易时刻的收益率。
标量BEKK 模型为: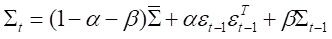 ,
,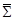 是无条件协方差,α,β是标量的参数,
是无条件协方差,α,β是标量的参数,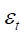 为收益率的残差向量,
为收益率的残差向量, 为k*k的协方差阵。
为k*k的协方差阵。
将已实现协方差阵RCOV代入到BEKK模型中,得到: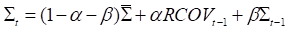
2.同理,BEKK-TSCOV形式为: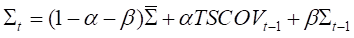
三、实证研究
1,选取股票数据,剔除交易缺失数据。
2.股票收益率以及预测协方差阵的描述性统计分析(均值、最大值、最小值、一阶自相关系数、标准差、峰度、偏度、JB检验P值)
3.构建投资组合采用等比例风险投资组合:通过不断调整资产的权数,使得在资产组合中每个资产的风险比例相同。
4.组合收益和波动分析:将预测的协方差阵代入到等比例风险投资组合中,看可以得到所选取12支股票的投资权重,进一步可计算出投资组合的收益和波动。并给出其Sharp比率值。Sharp比率是可以同时考虑风险和收益的综合指标,其值越大表明:收益一定的情况下,风险越小;或风险一定的情况下,收益越大。
5.稳健性分析
四、结论
无论投资组合的调整周期是日、周还是月,BEKK-TSCOV模型和BEKK-RCOV模型构造的资产组合的波动明显小于BEKK模型,说明在估计过程中引入高频数据的BEKK模型,明显提高了协方差阵的估计效率。在收益一定的情况下,由其构造的投资组合的风险更小,此外,BEKK-TSCOV模型的资产组合波动明显小于BEKK-RCOV模型,说明将高频数据引入到BEKK模型的估计过程中,噪声的影响不可忽略,BEKK-TSCOV模型剔除了噪声的影响,所以估计效果更优。
-------------基于高维数据的改进CCC-GARCH模型的估计及应用 刘丽萍,马丹,唐晓彬,2016-------
一、背景
当资产维度较高、数据量很大时,协方差阵的估计讲面临着维数诅咒,噪声等影响,传统的协方差阵估计和预测模型不再适用。CCC-GARCH 模型是由Bollerslev提出的常条件相关性模型 ,是常见的用以估计和预测金融资产协方差阵的多元 GARCH 模型。但是,当考虑的资产维度较高、数据量较大时, CCC-GARCH模型将不再适用。本文作者对CCC-GARCH模型进行改进,将主成分和门限方法应用在CCC-GARCH模型的估计中,提出主成分正交补门限CCC-GARCH(PTCCC-GARCH)模型。主要是将矩阵的谱分解方法应用到 CCC-GARCH的相关性矩阵的估计中,以提取其主要信息而达到降维的目的;然后将门限函数应用到矩阵的正交补中,以剔除噪声的影响。
二、模型
1.PTCCC-GARCH 模型主要是通过提取少数几个主成分来揭示高维资产间的关系,达到降维的目的;通过引入门限函数来剔除噪声的影响,使得高维协方差阵的估计得以实现。
2.对于主成分k的选择,采用均方误差MSE作为评价标准,损失函数MSE有效地衡量了PTCCC-GARCH估计的动态协方差阵与基于模拟数据的真实协方差阵的差异,差异越小表示模型的估计效果越好。最优的主成分个数k应该是使MSE的值最小。采用数值搜索法,不断进行搜索,寻找最优的主成分个数K。主成分K的选择直接影响到模型的估计效果。
三、实证研究
1.采用滚动时间窗方法,预测出PTCCC-GARCH模型和CCC-GARCH模型相对应的协方差阵,构造出投资组合。
2.组合效率的评价标准:夏普比率:反映组合风险与收益关系的指标;效用函数:衡量不同投资组合的经济福利。
3.本文采用最小方差和等比例风险投资组合
四、结论
PTCCC-GARCH模型的估计和预测效果与主成分 K 的选择密不可分,当 K 取到最优的数目时,PTCCC-GARCH模型便具有最优的表现,即便 K取1,PTCCC-GARCH模型的估计效率都要明显高于CCC-GARCH 模型;通过实证研究发现:无论选择最小方差投资组合还是等比例风险投资组合,较CCC-GARCH模型而言,根据 PTCCC-GARCH 模型所构造的投资组合的平均收益较高,波动较小,并且所对应的sharp比率明显要高于 CCC-GARCH模型。由PTCCC-GARCH模型所构造的投资组合明显优于CCC-GARCH模型,所获得的组合收益和经济福利更高。总之, PTCCC-GARCH模型提高了高维 协 方 差 阵 的 估 计 和 预 测 效 率,克 服 了 CCC-GARCH模型的不足。