学习文献：
Time-Varying Parameter VAR Model with Stochastic Volatility:An Overview of Methodology and Empirical Applications，
Jouchi Nakajima(2011)
一、
VAR:向量自回归模型，结果仅具有统计上的 意义
SVAR：结构向量自回归模型
TVP-VAR：Time Varying Parameter-Stochastic Volatility-Vector Auto Regression。时变参数随机波动率向量自回归模型，与VAR 不同的是，模型没有同方差的假定，更符合实际。并且时变参数假定随机波动率，更能捕捉到经济变量在不同时代背景下所具有的关系和特征（时变影响）。将随机波动性纳入TVP估算中可以显着提高估算性能。在VAR模型中，所有的参数遵循一阶游走过程。
随机波动的概念在TVP-VAR中很重要，随机波动是1976年由Black提出，随后在经济计量中有很大的发展。近几年，随机波动也经常被用在宏观经济的经验分析中。很多情况下，经济数据的产生过程中具有漂移系数和随机波动的冲击，如果是这种情况，那么使用具有时变系数但具有恒定波动性的模型会引起一个问题，即由于忽略了扰动中波动性的可能变化，估计的时变系数可能会出现偏差。为了避免这种问题，TVP-VAR模型假设了随机波动性。尽管似然函数难以处理，所以随机波动率使估计变得困难，但是可以在贝叶斯推断中使用马尔可夫链蒙特卡罗（MCMC）方法来估计模型。
从 具有随机波动性的时变参数（TVP）回归模型的估计算法(TVP-VAR模型的单变量情况)说起。
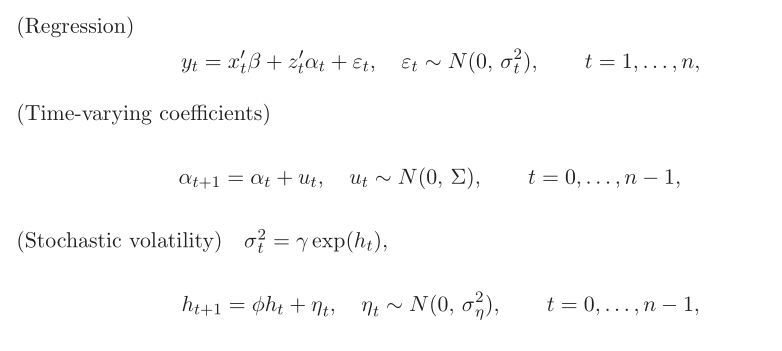
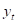是反应的标量，
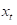是k×1的协变量向量，
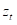是p×1的协变量向量。β是k×1的常系数向量；
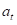是p×1的时变向量；
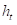是随机波动。
假设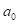
=0，
。
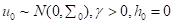式1中，β部分是常系数向量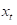，对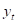的影响是假设不随时间变化而变化的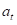；部分是时变向量，假设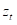对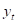的回归关系是时变的。
时变系数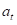假设遵循式2中的一阶随机游走过程。漂移系数可以捕获可能存在的非线性，例如结构破坏。也就是说，时变系数可以捕获真正的移动以及虚假移动。也就是说，如果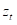和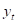的关系不清楚，可能会出现过拟合。
对于回归的干扰项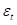
，服从随时间变化的正态分布
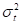。对数波动率
。
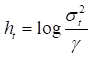二、MCMC算法
MCMC算法，一种随机采样方法，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。MCMC方法是用来在概率空间，通过随机采样估算兴趣参数的后验分布。
MCMC方法是在贝叶斯推断的背景下考虑的，其目标是在研究人员预先设定的特定先验概率密度下评估目标参数的联合后验分布。
在贝叶斯推断中，为未知参数θ的向量指定先验密度，用π（θ）表示。用f(y|θ)表示数据y = {y 1 ,...,y n }的似然函数。然后根据先验分布进行推断，用 π(θ|y)表示。
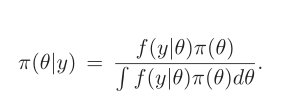
MCMC算法通过递归采样条件后验分布来进行，其中在仿真中使用了条件参数的最新值。
Gibbs采样器是著名的MCMC方法之一。步骤如下：
对于MCMC算法，π(θ)为先验密度，后验分布 π(θ,α,h|y）^4。
(具体参数参考Nakajima原文)
三、TVP-VAR Model
首先考虑SVAR model的定义：
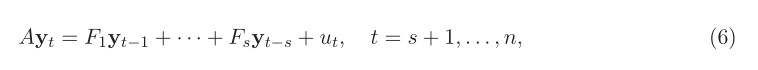
yt是k×1的观察变量，A，F是k×k的系数矩阵，扰动项ut是k×1的结构性冲击，假设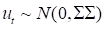
，
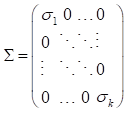
假设A为下三角矩阵，通过递归识别指定结构冲击的关系。
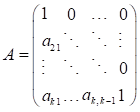
所以，式6可以写为：
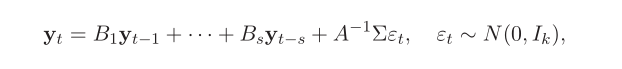
其中，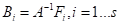
，定义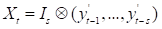
，（ Kronecker乘积）。
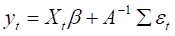（7）
式7中，所有的参数都是时变的。所以，TVP-VAR模型：
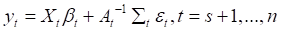（8）
，
，
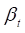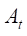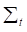都是时变的。
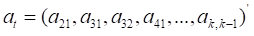是下三角矩阵，
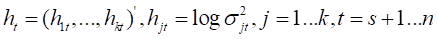
式8中的参数都遵循以下随机游走过程：
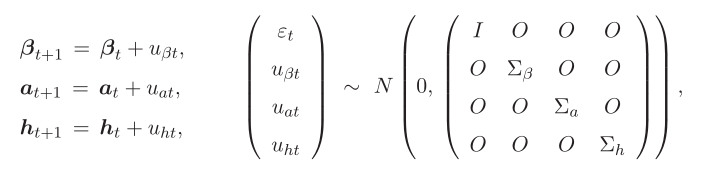
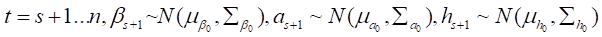
注意：
1.假设参数服从随机游走过程
2.时变参数的方差和协方差结构由参数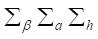
控制。许多文章中假定
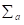是对角矩阵。
3.当在贝叶斯推断中实现TVP-VAR模型时，应谨慎选择先验，因为TVP-VAR模型具有许多状态变量，并且其过程被建模为非平稳随机游走过程TVP-VAR模型非常灵活，状态变量可以捕捉潜在经济结构的渐进和突变。但是在VAR模型中的每个参数中允许时间变化可能会导致过度识别问题。
四、进行TVP-VAR建模时，也需要数据平稳。可以用ADF单位根检验法检验数据的平稳性，不平稳的数据可以做差分，直至平稳，用差分后的数据进行建模。
需要注意的是：TVP-VAR建模时，变量之间的顺序会影响到最后的实证结果。变量的顺序问题可能是实证结果不符合预期的一个原因。最好把关注的变量放在首位，这样在时变关系图中就能得到较好的展示。