在一些经典算法中,经常需要判断一些图是否具有环路,比如拓扑排序,需要在最初判断该图是否有环路,如有有环路,则无法找到最长的一条线,比如dijkstra算法,每找到一条最短的边,都要判断找到的边和现有的树是否已经构成了环路。
因此,在这篇博客,我们重点来说一个判断图是否有环的算法。
首先我们介绍一个对于无向图和有向图通用的算法,先讲算法思路:
1.统计各个图中各个点的入度数(能够到达这个点的点的数量)。
2.然后找出入度数为0的点(无向图找入度数为1的点)。
3.删除入度数为0的点,将其边也删除。
4.重复2,直到所有点入度都为0,则为无环图,如果找不到入度为0的点,则为有环图。
该算法的精髓在于对于一个环路(以有向图为例),1->2,2->3,3->1,你会发现找不到一个入度为0的点,因此这个方法是可行的。
对于无向图和有向图来说,这个算法是通用的。在这我只写了对于有向图的判断的算法,具体的实现代码如下:
#include<stdio.h>
using namespace std;
int graph[100][100];//用来存储图的数组
bool isVisited[100];//判断这个点是否已经删除
int main()
{
int n,e;
while (scanf("%d",&n)!=EOF&&n!=0)//获取点数
{
for(int i = 0;i<100;i++)
{
isVisited[i] = false;
for(int j = 0 ;j<100;j++)
{
graph[i][j] = -1;//初始化数据,所有的边都为-1,代表这两个点之间不能联通
}
}
scanf("%d",&e);//获取边数
for(int i = 0 ;i<e;i++)//构建图
{
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
graph[a-1][b-1] = c;
}
int isResult = true;
for(int i = 0 ;i<n;i++)//进行n次循环,每次循环删除一个入度为0的点,所以进行n次循环
{
for(int j = 0;j<n;j++)//遍历所有的点,找入度为0的点
{
if(!isVisited[j])//判断该点是否删除
{
bool isCanVisited = true;//辅助变量,判断这个点是否入度为0
for(int k = 0;k<n ;k++)
{
if(graph[k][j]!=-1)
{
isCanVisited = false;//如果存在能够访问这个点的边,则该点入度不为0
}
}
if(isCanVisited)//如果该点入度为0,则下边是删除该点和删除其相邻边
{
for(int k = 0 ;k<n;k++)
{
graph[j][k] = -1;//删除相邻边,即将值变为-1
}
isVisited[j] = true;//删除该点
}
}
}
isResult = true;
for(int j = 0 ;j<n;j++)//进行循环判断当前多有点是否已经全部删除,如果全部删除,如果全部删除则跳出,否则继续循环
{
if(!isVisited[j])
{
isResult = false;
}
}
if(isResult)
break;
}
isResult = true;
for(int i = 0 ;i<n;i++)//在所有点遍历后,则通过这个循环来判断是否所有点都已经删除,如果全部删除,则为无环图,否则为有环图
{
if(!isVisited[i])
isResult = false;
}
if(isResult)
printf("无环");
if(!isResult)
printf("有环");
}
return 0;
}
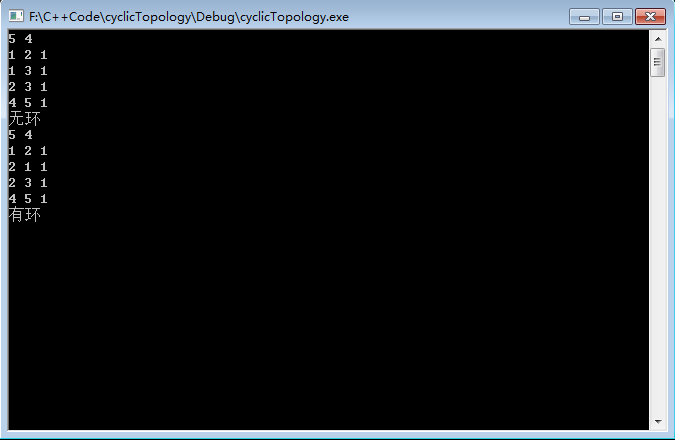
实验数据(第一行输入n,e,n代表的是点数,e代表的是边数,接下来e行代表具体的边和其权值(权值暂时不用理会,是后续拓扑排序所有,因此当前暂时都为1)):
5 4
1 2 1
1 3 1
2 3 1
4 5 1
5 4
1 2 1
2 1 1
2 3 1
4 5 1
实验结果: