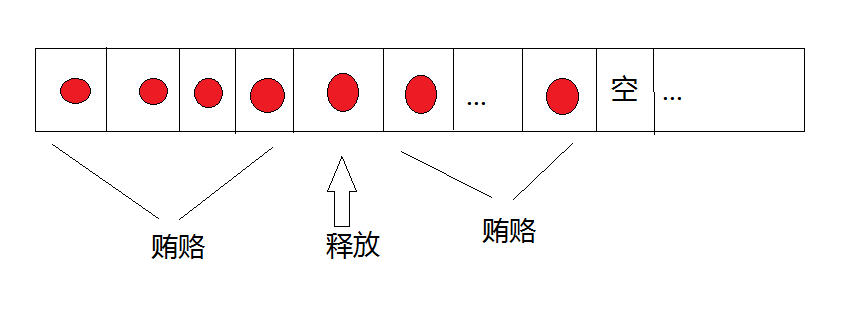
一个监狱里有P个并排着的牢房,从左往右一次编号为1,2,…,P。最初所有牢房里面都住着一个囚犯。现在要释放一些囚犯。如果释放某个牢房里的囚犯,必须要贿赂两边所有的囚犯一个金币,直到监狱的两端或者空牢房为止。现在要释放a1,a2,...,aQ号囚犯,如何选择释放的顺序,使得使用的金币最少。
思路:
其中很重要的一点:释放了某个囚犯以后,就把连续的牢房分成了没有任何关系的两段。
只要枚举出所有的释放囚犯的顺序即可,复杂度为 O(Q3)。
利用动态规划枚举所有的情况的时候,我们有2种方法:
方法1.(自上而下)先选取首先释放的囚犯。然后划分没两段独立的部分,然后对左右两段再递归的调用。
方法2.(自下而上)利用动态规划数组,例举出所有最小的子问题,然后再根据最小的子问题可以组合成稍大一点的子问题。
用二叉树的来表示可能更形象一点:
针对每个释放顺序,都可以用一个二叉树来表示
例如:有 1-8个囚犯,释放顺序为:4,2,6的话
1、先释放4
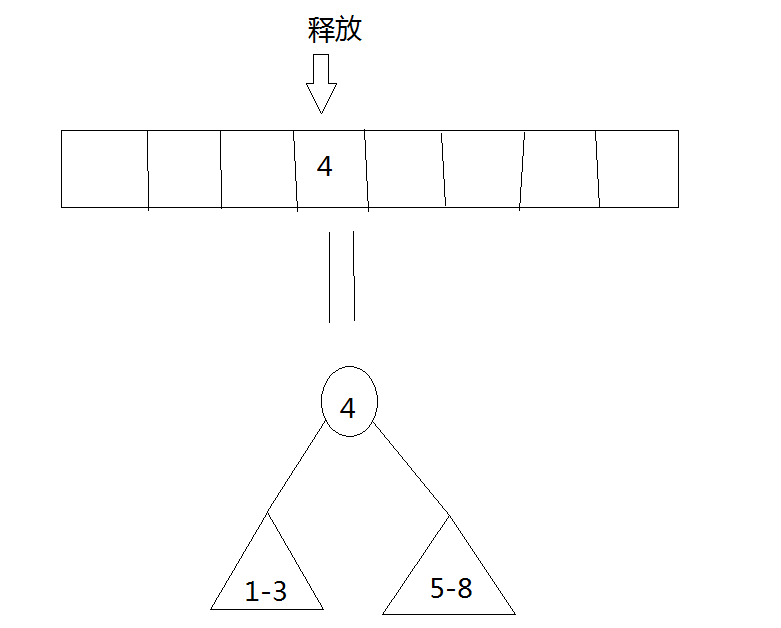
2、释放2
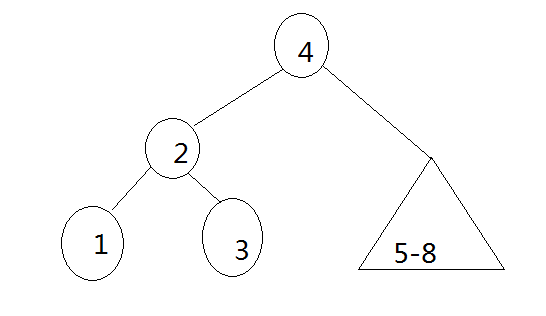
3、释放6
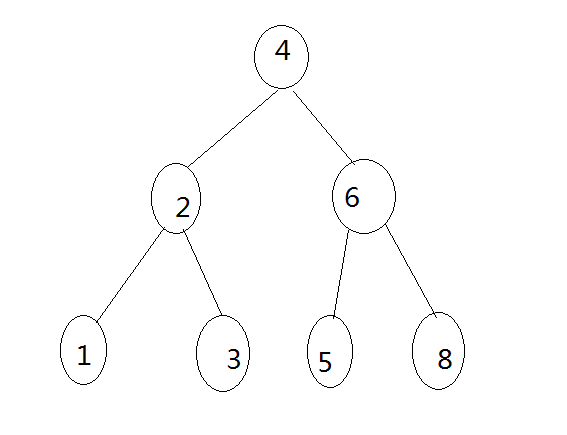
可以看出,当释放4号的时候,就把原先的1-8号分为1-3号和5-8号两段独立的,所以上面的第二步和第三步其实可以交换的,
当然这个例子比较简单,不过其实再复杂的问题也就是上面的这些情况的不断叠加而已,比如上面这个二叉树也可能是更大的二叉树的一个部分。
然后我们再回过来,用二叉树的表示方法来再来说一下上面的2个方法,可能方法1比较容易理解,人的一般思维方式都是这样的,然后重点说说方法2
方法2的思想是:
例如要释放 a1,a2,...,aQ囚犯,我们记为A[1]-A[Q],先分成最小的区间开始找,为了方便,我们把两端也加入,这样变为A[0]-A[Q+1]
什么叫最小的区间?就是在区间里面只有一个要释放的囚犯,这样的区间(长度为2)是 A[0]−A[2],A[1]−A[3]..A[Q−1]−A[Q+1],求出其对应的金币,我们记为Cost[0][2],Cost[1][3]...Cost[Q−1][Q+1]
然后我们再找区间里面只有两个要释放的囚犯,这样区间(长度为3)可以用上面长度为2的区间来求得 例如 A[0]-A[3]
如果先释放1号,对应的是Cost[1][3]加上a0与a1之间的囚犯数
如果先释放2号,对应的是Cost[0][2]加上a2与a3之间的囚犯数
然后Cost[0][3]就是上面值更小的一个情况
这样不断迭代,最后就可以求出Cost[0][Q+1],就是最后的答案
枚举的时候,由于可能会出现多次相同的情况,但前面又已经计算过了,所以可以利用一个数组,来保存已经计算过的情况(剪枝)。
代码:
#include<stdio.h>
#define INT_MAX 0x3f3f3f3f
using namespace std;
int p,Q ;
//区间动态规划
//bribe the prisoner
//定义一个二维数组。依次用来填充最小的花费。
int dp[109][109];//表示从第i个填充到j个时的最小花费。
//同时定义一个存放罪犯的数组。
int a[109];
void solve()
{
a[0]=0;
a[Q+1]=p+1;//为了解决边界问题。
for(int i=0; i<=Q; i++)
dp[i][i+1]=0;//初始化,因为所有的从i到i+1的花费除去边界都是0;
//循环求解。定义w表示区间的范围,w=2表示跨度为2的情况,也就是该区间里面只有一个要释放的犯人
for(int w=2; w<=Q+1; w++)
{
//每次选的范围都是w,从i到j 的范围内的最小值等于从i到K加从第k到j的最小值。
for(int i=0; i+w<=Q+1; i++)
{
//此处用到的k恰是其中的中值。
int j=i+w,tmp=INT_MAX;//tmp用来保存当前区间的当前最好情况的花费金币数
for(int k=i+1; k<j; k++)
tmp=min(tmp,dp[i][k]+dp[k][j]);
dp[i][j]=tmp+a[j]-a[i]-2;//此处就是当前区间最小值。
}
}
printf("%d
",dp[0][Q+1]);
}
int main()
{
scanf("%d%d",&p,&Q);
for(int i=1; i<=Q; i++)
scanf("%d",&a[i]);
solve();
return 0;
}