话题引入:最大传输量
网络中有两台计算机s和t,现在想从s传输数据到t。该网络中一共有N台计算机,其中一些计算机之间连有一条单向的通信电缆,每条通信电缆都有对应的1秒钟内所能传输的最大数据量。当其他计算机之间没有数据传输时,在1秒内s最多可以传输多少数据到t?

分析:
把计算机当作顶点,把连接计算机的通信电缆当作边,就可以把这个网络当作一个有向图来考虑了。图中的每条边e∈E都有对应的最大可能的数据传输量c(e)。这样,就可以把问题转换为如下形式。
·记每条边对应的实际数据传输量为f(e)。
·传输量应该满足如下限制:
0<=f(e)<=c(e)
·数据在传输过程中既不会增加也不减少,收到的数据量和发出的数据量应该相等。
·我们应该尽可能的目标最大化从s发出的数据量。
称使得传输量最大的f为最大流,而求解最大流的问题为最大流问题。此外,我们称c为边的容量,f为边的流量,s为源点,t为汇点。那么,我们首先考虑贪心算法来求解
1.找一条s到t的只经过f(e)<c(e)的边的路径;
2.如果不存在满足条件的路径,则结束算法。否则,沿着该路径尽可能地增加f(e),返回第(1)步。
将该算法运用于样例,就得到了如下结果

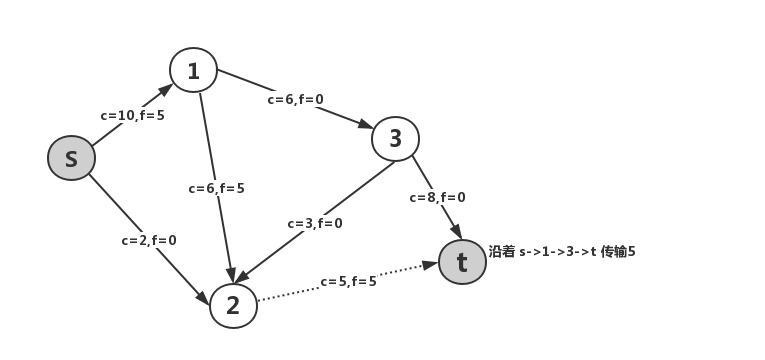

那么,我们考虑一下这样得到的就是最大流吗?事实上,如果采用下图所示的方案,可以达到更优的结果,于是知道这个贪心算法是不正确的。

可以看出来,贪心算法的到的结果是10,而上图的到的结果是11.那么找出二者的区别,不妨来看看他们的流量差。

通过对流量的差的观察可以发现,我们通过将原先的到的流给推回去(图中的-1部分),而得到了新的流。因此,可以试着在之前的贪心算法中加上这一操作,将算法进行如下改进。
1.只利用满足f(e)<c(e)的e或者满足f(e)>0的e对应的反向边rev(e),寻找一条s到t的路径。
2.如果不存在满足条件的路径,则结束。否则,沿着该路径尽可能的增加流,返回第(1)步。
将改进后的算法用于样例。
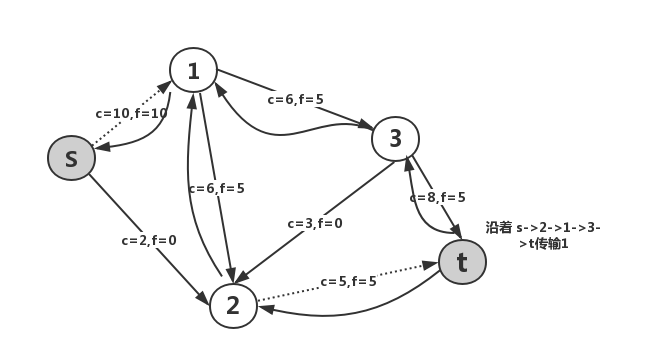
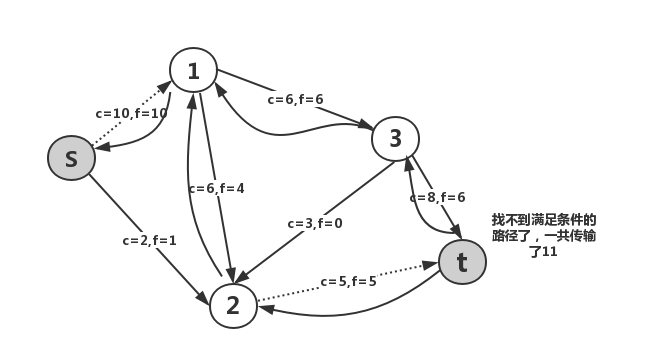
这样就得到了11这一结果,而且这一算法是总能求得最大流的。将这个求解最大流问题的算法称为Ford-Fulkerson算法。另外,称在(1)中所考虑的f(e)<c(e)和满足f(e)>0的e对应的反向边rev(e)所组成的图称为残余网络,并称残余网络上的s-t路径为增广路。
代码:
#include<iostream>
#include<stdio.h>
#include<vector>
#include<string.h>
#define inf 0x3f3f3f3f
using namespace std;
int n,m;
struct edge
{
///分别表示终点,容量,反向边
int to,cap,rev;
};
vector <edge> G[100];///图的邻接表表示
bool used[100];
///向图中增加一条从s到t容量为cap的边
bool add_edge(int from,int to,int cap)
{
G[from].push_back((edge){to,cap,G[to].size()});
G[to].push_back((edge){from,0,G[from].size()-1});///反向边的最大的容量应该设置为0,因为这条边本来是不存在的
}
///通过dfs寻找增广路
int dfs(int v,int t,int f)///起点,终点,流量
{
if(v==t) return f;///起点和终点相等的话,流量是没有变化的
used[v]=true;///标记这个点已经走过
for(int i=0; i<G[v].size(); i++)///遍历以这个点为起点的所有的边
{
edge &e=G[v][i];
if(!used[e.to]&&e.cap>0)///这个点没有访问过,并且还有流量呢
{
int d=dfs(e.to,t,min(f,e.cap));///接着往下遍历
if(d>0)///这次遍历所消耗的流量
{
e.cap-=d;
G[e.to][e.rev].cap+=d;
return d;
}
}
}
}
///从s到t的最大流
int max_flow(int s,int t)
{
int flow=0;
for(;;)
{
memset(used,0,sizeof(used));
int f=dfs(s,t,inf);
if(f==0)
return flow;
flow+=f;
}
}
int main()
{
int u,v,w,s,t;
scanf("%d%d",&n,&m);
memset(G,0,sizeof(G));
while(m--)
{
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w);
}
scanf("%d%d",&s,&t);
printf("%d
",max_flow(s,t));
return 0;
}
最小割
为了证明Ford-Fulkerson算法所求得得确实是最大流,我们首先介绍割这一概念。所谓图的割,指的是对于某个定点集合S包含于V,从S出发指向S外部的那些边的集合,称为割(S,VS)。这些边的容量之和被称为割的容量。如果有s∈S,而t∈VS,那么此时的割又称为s-t割。如果将网络中s-t割所包含的边都删去,也就不再有从s到t的路径了,因此,考虑一下如下问题:
对于给定网络,为了保证没有从s到t的路径,需要删去的边的总容量的最小值是多少?
该问题又被称为最小割问题。事实上,这个问题与之前的最大割问题有着很深的联系。
首先,我们来考虑一下任意的s-t流f和任意的s-t割(S,VS)。因为有(f的流量)=(s的出边的总流量),而对v∈S{s}又有(v的出边的总流量)=(v的入边的总流量),所以有(f的流量)=(S的出边的总流量)-(S的入边的总流量)。由此可知(f的流量)<=(割的容量)。
接下来,让我们来考虑通过Ford-Fulkerson算法所求得的流f'。记流f'对应的残余网络从s可达的顶点v组成的集合为S,因为f'对应的残余网络中不存在s-t路径,因此(S,VS)就是一个s-t割。此外,根据S的定义,对包含在割中的边e应该有f'(e)=c(e),而对从VS到S的边e应该有f’(e)=0。此外,(f'的流量)=(S的出边的总流量)-(S的入边的总流量)=(割的容量),再由之前的不等式可以知道,f'即是最大流。
于是我们证明了Ford-Fulkerson算法的正确性。同时还推导出了最大流等于最小割这一重要性质。改性质又被称为最大流最小割定理。此外,由Ford-Fulkerson算法的正确性可以知道,如果所有边的容量都在整数,那么最大流和最小割也是整数。