项目地址:https://gitee.com/Shanyalin/pdf-tranlate
上一篇博客的部分遗留问题,我需要在此明确一下。
单纯使用pymupdf来解决pdf提取问题,是很困难的。比如表格,就是个很难绕过的问题。这里会逐步引入一些已经证实的解决方案。
首先,重申一次pdf 翻译的思路及注意事项。翻译,因为翻译api的泛滥,不再做赘述。核心重点在内容提取,文本整合,内容输出。
内容提取,注意不再是文本提取了。这次不仅要将文本、图片提取,也要将表格、自定义的绘画(draw)也提取出来。在内容上尽可能的向原始文件靠近。
文本整合,由于提取出了表格,所以表格内的内容尽可能保持原样,不做整合。表格外的内容,尽可能以段落为单位,一页一页提取整合,提高翻译的准确性。
内容输出,在上一篇博客中定下了原样输出的原则,本次依然在此基础上,将表格及自定义的绘画都还原出来。
接下来先介绍一下相对简单的内容——自定义绘画。
pymupdf的Page.get_drawings()可以提供页面中自定义绘画相关的类型,位置,颜色等一系列相关参数。详细可以参考:Page.get_drawings
其中items是个元组列表,元组的第一个字段表示绘画类型,后续字段都是位置相关信息。l表示线段,后两个参数是两个point。re表示rect矩形,后续参数是个rect_like,可以直接画rect。c表示贝泽尔曲线,四个点分别是 起点,控制点1,控制点2,终点。
Page有相关的绘画api,如画线段的draw_line,画矩形的draw_rect,画曲线的draw_bezier()。注意:目前测试过程中,图片的边框也会被读出为矩形,将矩形画出并填充之后,再向同区域添加图片会被覆盖或失败,即使图片在画完矩形后添加也会有异常,总之就是不显示,使用时需要注意,当然也可以自己尝试后确认。相关代码可以参考:Drawing and Graphics
自定义绘画的使用介绍告一段落,接下来介绍表格的提取。
表格的提取有两套经过验证的方案,且各自都经过了验证。
| 详细解决方案 | 优点 | 缺点 |
| 根据观察表格内容的文本提取结果,以span和line为观察对象,总结一定的规则,不断的对规则进行扩充,对表格进行定义,使定义的规则可以囊括大多数情况。通过不断的迭代,形成一套相对准确的提取方案。 | 通过简单定义表格规则来提取表格。通过不断迭代来完善规则。开发起来简单,没有额外引入风险。 | 规则定义不完善,总有表格可以突破定义,造成疏漏。需要对规则大量迭代回归,效率较低。准确率较低。 |
| 通过机器学习进行文档分析。文档分析是以分析图片进行处理,首先将pdf页转成jpg文件,通过分析图片返回表格坐标及相应评分。可以根据评分来判断是否采用此表格分析。 | 通过已经成熟训练过的机器学习模型进行图片分析,提取表格,准确度高。 | 环境部署相对困难,有额外引入风险。机器学习相关环境需要gpu,无法在win环境下开发部署 |
经过一段时间观察和整理,认为文本在提取过程中不应该以block为单位,部分pdf会将多行文本直接提取到一个block中。这种现象某种程度上来说是好事,但是在对于表格提取上反而是个障碍。最终决定在文本提取时,以block下的lines的span为最小单位。近期的实践过程中没有发现需要以字符为最小单位进行拼接的情况,所以没有必要使用get_text('rawdict')来获取字符。dict的结构如下图:
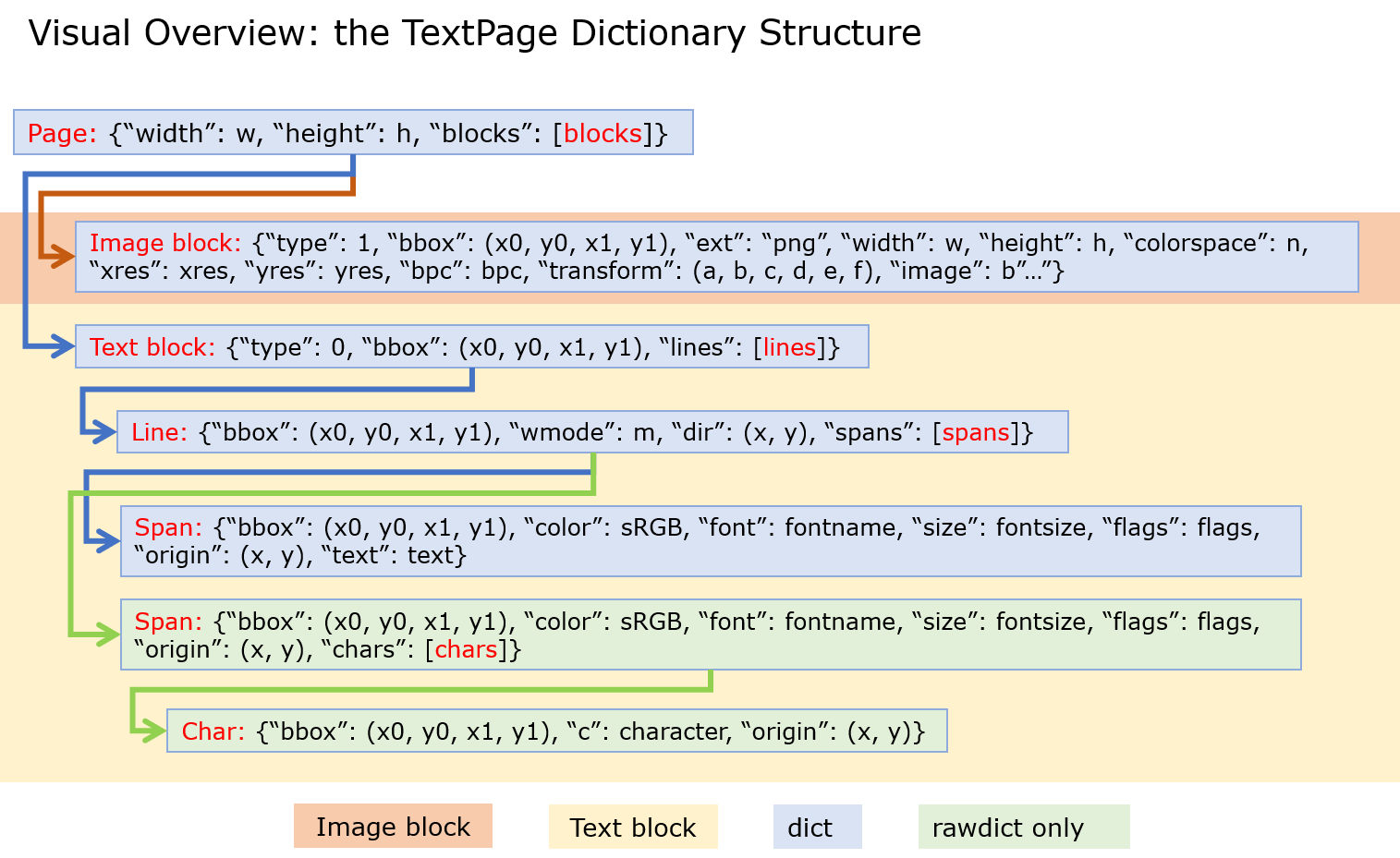
将dict重组成最基础的block结构代码如下,相较于上个版本直接进行提取,这次考虑了block中多行的情况,主动对多行现象进行了切分。当判断文本在表格范围内的时候,即放弃整合。in_tables(rect,tables)方法可在项目文件中查看。
def dicts2blocks(extract_dict, tables=[]): blocks = extract_dict['blocks'] blks = [] for d in blocks: bbox, type, fz, text = d['bbox'], d['type'], 0, '' if type == 0: # 文本 lines = d['lines'] blk_lines = [] for l in lines: t_bbox = l['bbox'] if t_bbox[0] < 0 and t_bbox[2] < 0: continue # 两个横坐标都小于0 if in_tables(t_bbox, tables): for s in l['spans']: t_text = s['text'] t_fz = s['size'] t_bbox = s['bbox'] blk_lines.append((t_bbox, t_text, t_fz)) else: t_text = ''.join([s['text'] for s in l['spans']]) t_fz = max([s['size'] for s in l['spans']]) blk_lines.append((t_bbox, t_text, t_fz)) pre_bbox, pre_text, pre_fz = None, '', 0 for i, bl in enumerate(blk_lines): if i == 0: pre_bbox, pre_text, pre_fz, = bl continue curr_bbox, curr_text, curr_fz, = bl if not in_tables(pre_bbox, tables): if abs(pre_bbox[1] - curr_bbox[1]) <= curr_fz * 0.2 and abs( pre_bbox[3] - curr_bbox[3]) <= curr_fz * 0.2: # baseline 有轻微高低差不能使用origin_y判断 # 同行且字体大小一样 if abs(curr_bbox[0] - pre_bbox[2]) <= curr_fz * 5: # 当前box 在上一个box的右侧4个字符以内 应合并 pre_bbox = (min(pre_bbox[0], curr_bbox[0]), min(pre_bbox[1], curr_bbox[1]), max(pre_bbox[2], curr_bbox[2]), max(pre_bbox[3], curr_bbox[3])) pre_text += curr_text pre_fz = max(pre_fz, curr_fz) continue blks.append((pre_bbox[0], pre_bbox[1], pre_bbox[2], pre_bbox[3], strQ2B(pre_text) + ' ', pre_fz, type)) pre_bbox, pre_text, pre_fz = curr_bbox, curr_text, curr_fz blks.append((pre_bbox[0], pre_bbox[1], pre_bbox[2], pre_bbox[3], strQ2B(pre_text) + ' ', pre_fz, type)) else: # 非文本 blks.append((bbox[0], bbox[1], bbox[2], bbox[3], strQ2B(text) + ' ', fz, type)) return blks
整合文本的过程也添加了对表格范围的判断。改动较小不再展示代码。
下面介绍一下解决方案一,核心就是定义表格规范。从dict中提取出来的span,我们通过什么来认定这些是表格。
这里直接说结论,通过观察迭代,我们认定符合这样的条件的是表格。
一.表格分布在一个block中,表头也在block中。此时我们认为表格最极端的形状是3行2列。
特点:1.一个block中有多行(至少三行),且每行中有多个span,总span的个数至少有6个;
2.span的最大建议宽度取block的1/3和100的最小值(pymupdf中宽度的单位应该是px,未证实,所以用统一单位来代替,避免歧义),最大建议宽度的设置是为了避免有些相对极端的情况。至于为何取block的1/3,当span宽度超过1/3之后,每行最多有2个span,表格的形状就变成了3行2列最极端的情况,再极端就变成了6行1列,或者2行3列(表头占一行)这些情况,显然不能将这些认为是表格;
二.表格分布在相邻的多个block中,表头或许不在相邻block中,此时我们认为表格最极端的形状是2行3列。尽管2列也可以,但是2列在处理的时候容易命中错误。
特点: 1.相邻行的span个数大于3,且span个数相等。
2.相邻行对应的span宽度应该是接近的,较大宽度是较小宽度的1.6倍,且超过个数不能超过2个。设置宽这样的阈值是避免对应span中的内容出现多个极长对极短的现象。
3.同一行中,最大span和最小span的宽度倍率限制为8,但出现次数不能超过2个。
关于倍率和次数的限制在后来实践过程中屡次被突破,后来将阈值设置为倍率*次数,计算方法不再单纯以次数来判断,而是以实际倍率加和来判断。例如同一行中最大span是最小span的20倍,超过8倍的仅出现了一次,这种情况下可以将他看作表格吗?大概率是不行的(通过观察获得的结论)。再如,两行文本被识别成span个数一样,最小span内容是一个标点,那最小span的宽度作为倍率的基准是否合适呢?显然是不合适的,因为这两行本质就是文本,不是表格,他的前置条件就错了。
以上两种情况是可以通过解决方案一来识别出来的,也是常见的大多数情况。下面说一下不能被识别的情况。
1.表格单元格的内容是多行,且行数不等。这种情况,一个单元格会被识别成一个block,其中的内容通常是多行,每行一个或多个span。表格的单元格之间是平行的关系。观察上面可以解决的情况,这种平行关系是识别不了的。因为不能确定当前block的坐标跟上一个block的坐标是否在一个表格里(可以确定不是同一行,也可以确定不是同一列,但是无法确定不能确定在同一个表格,因为至少需要向前追溯N-1个block,N为列数)。
2.表格的读取是以单元格为单位,从上到下从左到右。因为pymupdf的提取习惯也是这样,那么判断表格就需要回溯N个block,这个在实现上几乎是不可能的,也是不必要的。
3.表格提取的内容是以字符为单位,无法通过block或者span来识别表格。
4.表格是2列的。如果设置列数为2,很多文本会误中副车,导致后期合并文本出现问题。这种情况只能宁纵勿枉,不能错杀。
讲述了2种常见适用情况和4种少见情况,详见代码的处理如下:
def gettables(extract_dict): tab = [] blocks = extract_dict['blocks'] for i, b in enumerate(blocks): if i == 0: bbox_p = b['bbox'] spans_p = [s['bbox'][2] - s['bbox'][0] for l in b['lines'] for s in l['spans'] if s['text'].strip()] if b[ 'type'] == 0 else [bbox_p[2] - bbox_p[0]] height_p = bbox_p[3] - bbox_p[1] continue if b['type'] == 0: bbox_c = b['bbox'] spans_c = [s['bbox'][2] - s['bbox'][0] for l in b['lines'] for s in l['spans'] if s['text'].strip()] height_c = bbox_c[3] - bbox_c[1] fontsize_b_c = max([s['size'] for l in b['lines'] for s in l['spans']]) # ------------------将表格放到一个block中----------------------- if height_c / fontsize_b_c >= P_line_block and len(spans_c) >= P_spans_block: # 特殊情况 当前block 至少有3行文本 且span 数量大于6,可以按表格处理 bbox_p, spans_p, height_p = bbox_c, spans_c, height_c weight_block = bbox_c[2] - bbox_c[0] limit = min(weight_block / 3, P_span_width_block) if sum([int(w / limit) for w in spans_c if w >= limit]) > 2: # 任意一个span的宽度大于 block的33% 不以表格处理 # 超过block宽度30%的span应少于3个 continue tab.append(bbox_p) continue # ------------------表格分散在连续的block中------------------------ if len(spans_c) == len(spans_p) > P_spans_blocks: # 判断相邻行 对应span宽度比例不能超过1.6且超过个数不超过2 tmp = [max(spans_c[i], spans_p[i]) / min(spans_c[i], spans_p[i]) for i in range(len(spans_c))] # 判断当前行 最大span和最小span宽度比例 不能超过8 且个数不能超过2 min_span_w = max(min(spans_c), fontsize_b_c) min_ratio_c = [w / min_span_w for w in spans_c if w / min_span_w > P_span_min_width_ratio_blocks[0]] if sum([1 for t in tmp if t >= P_span_width_ratio_blocks[0]]) >= P_span_width_ratio_blocks[-1]: pass elif sum(min_ratio_c) >= P_span_min_width_ratio_blocks[0] * P_span_min_width_ratio_blocks[-1]: pass else: bbox_c = (min(bbox_p[0], bbox_c[0]), min(bbox_p[1], bbox_c[1]), max(bbox_p[2], bbox_c[2]), max(bbox_p[3], bbox_c[3])) elif len(spans_p) == 1: pass else: if bbox_p[3] - bbox_p[1] >= P_line_blocks * height_p: tab.append(bbox_p) bbox_p, spans_p, height_p = bbox_c, spans_c, height_c if bbox_p[3] - bbox_p[1] > height_c: tab.append(bbox_p) return tab
囿于篇幅,关于通过机器学习来识别表格的方法,下次再整理。
附图:
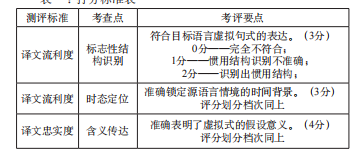
上图为不能识别的情况1.
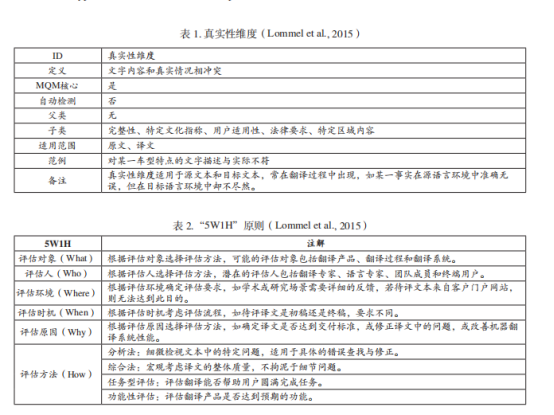
上图为不能识别的情况4
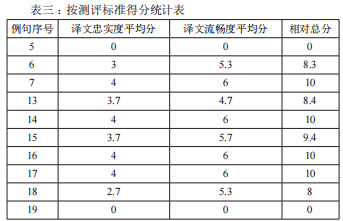
上图为相邻行对应span宽度倍率不超过1.6,不能解决的情况。