[LeetCode] 1503. Last Moment Before All Ants Fall Out of a Plank

We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with speed 1 unit per second. Some of the ants move to the left, the other move to the right.

When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions doesn't take any additional time.

When an ant reaches one end of the plank at a time t, it falls out of the plank imediately.

Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right. Return the moment when the last ant(s) fall out of the plank.

Example 1:

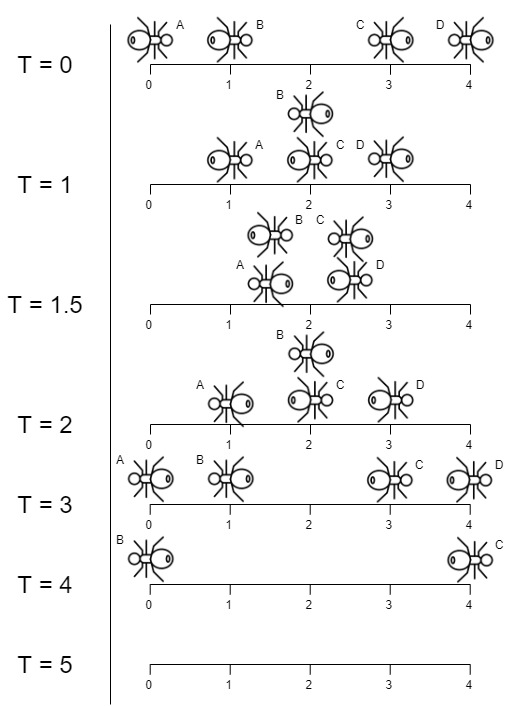
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
Note that the last moment when an ant was on the plank is t = 4 second, after that it falls imediately out of the plank. (i.e. We can say that at t = 4.0000000001, there is no ants on the plank).

Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

Example 4:

Input: n = 9, left = [5], right = [4]
Output: 5
Explanation: At t = 1 second, both ants will be at the same intial position but with different direction.

Example 5:

Input: n = 6, left = [6], right = [0]
Output: 6

Constraints:

• 1 <= n <= 10^4
• 0 <= left.length <= n + 1
• 0 <= left[i] <= n
• 0 <= right.length <= n + 1
• 0 <= right[i] <= n
• 1 <= left.length + right.length <= n + 1
• All values of left and right are unique, and each value can appear only in one of the two arrays.

所有蚂蚁掉下来前的最后一刻。

题意是问蚂蚁最多需要多长时间才能完全离开面板。如果你想通了，思路很简单。当蚂蚁相遇的时候，题意规定是两只蚂蚁需要向相反方向走，这个规则乍一看其实会让你感觉是不是会增加一个蚂蚁离开面板的时间，其实是不会的。当两只蚂蚁相遇，你可以把他视为如果是a和b相撞，可以将a和b相互调换一下位置，

a-> <-b === <-b a->

因为蚂蚁身上没有别的参数，两只蚂蚁相遇也没有什么代价，所以可以这样做。

时间O(nlogn)

空间O(1)

Java实现

class Solution {
    public int getLastMoment(int n, int[] left, int[] right) {
        Arrays.sort(left);
        Arrays.sort(right);
        if (left.length == 0 && right.length == 0) {
            return 0;
        }
        if (left.length == 0 && right.length != 0) {
            return n - right[0];
        }
        if (left.length != 0 && right.length == 0) {
            return left[left.length - 1];
        }
        return Math.max(left[left.length - 1], n - right[0]);
    }
}

JavaScript实现

/**
 * @param {number} n
 * @param {number[]} left
 * @param {number[]} right
 * @return {number}
 */
var getLastMoment = function (n, left, right) {
    left.sort((a, b) => a - b);
    right.sort((a, b) => a - b);
    console.log(left);
    console.log(right);
    if (!left.length && !right.length) {
        return 0;
    }
    if (!left.length && right.length) {
        return n - right[0];
    }
    if (left.length && !right.length) {
        return left[left.length - 1];
    }
    return Math.max(left[left.length - 1], n - right[0]);
};

LeetCode 题目总结