目录
引言:
为获得更好的识别效果,现对身份证含有个人信息区域进行提取,缩小识别范围,以此来提高识别精度和效率
一、获取身份证号区域矩形
身份证号区域矩形的获取,见上一篇文章:
身份证识别(一):身份证号定位
二、获取地址、出生年月、性别、名族、姓名区域矩形
1. 获取号码区域位置
在第一步得到的结果是一个旋转矩形RotatedRect,该矩形的属性如下:
Angle:矩形旋转角度(相对水平方向),顺时针旋转值为正,逆时针旋转值为负。
Center:矩形的中心
Size:矩形的尺寸
GetVertices():PointF[]类型,包含矩形的四个顶点坐标。
有了这些信息之后就可以以该矩形(以下称为标准矩形)为基准计算其它区域的相对位置。
2. 获取各个区域的包围矩形
由于标准矩形的顶点顺序不确定,所以选用标准矩形的中心作为参考点,然后计算地址区域中心的偏移量。
以住址区域为例:
偏移量的计算:
标准矩形的中心为rr.Center
若旋转角度为0
float w = (float)(rr.Size.Width * 0.8); //住址区宽度
float h = (float)(rr.Size.Height * 1.7);//住址区高度
float px = (float)(rr.Center.X - rr.Size.Height * 3.1);//住址区x坐标
float py = (float)(rr.Center.Y - rr.Size.Height * 2.4);//住址区y坐标
PointF center = new PointF(px,py);
RotatedRect rect = new RotatedRect(center,new SizeF(w,h),rr.Angle);若旋转角度不为0
float w = (float)(rr.Size.Width * 0.8 * Math.Cos(rr.Angle); //住址区宽度
float h = (float)(rr.Size.Height * 1.7* Math.Cos(rr.Angle));//住址区高度三、剪切目标区域
裁剪目标区域,即将目标矩形内的像素点复制到一幅与矩形相同大小,并保持水平的图像中,以方便进一步的识别。
对于旋转角度为0的矩形,只要以左上角顶点为中心依次将矩形区域复制到新图像即可。
对于倾斜的矩形,则需要先选取旋转中心,然后将矩形旋转至水平方向,然后在对像素点进行遍历复制。
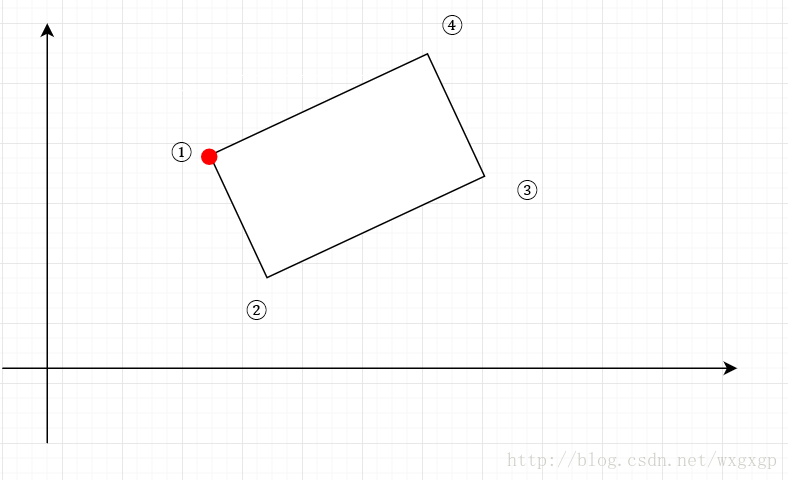
对于上一步得到的矩形,虽然GetVertices()可以获取四个顶点的坐标,但是无法确定顶点顺序,则无法确定旋转中心点,所以首先要对矩形顶点编号。我们按逆时针方向进行顶点编号。
这样当Angle<0编号为①的顶点就是旋转中心,当Angle<0编号为①的顶点就是旋转中心。
顶点编号主要代码:
/// <summary>
/// 矩形顶点编号
/// </summary>
/// <param name="pointfs"></param>
/// <param name="angle"></param>
/// <returns></returns>
public static PointF[] RectCode(RotatedRect rect)
{
PointF[] p = rect.GetVertices();
PointF[] pointfs = new PointF[4];
pointfs[0] = p[0];
pointfs[1] = p[0];
pointfs[2] = p[0];
pointfs[3] = p[0];
//逆时针编号
for (int i = 1; i < 4; i++)
{
if (p[i].X < p[i - 1].X)
pointfs[0] = p[i];
if (p[i].Y > p[i - 1].Y)
pointfs[1] = p[i];
if (p[i].X > p[i - 1].X)
pointfs[2] = p[i];
if (p[i].Y < p[i - 1].Y)
pointfs[3] = p[i];
}
return pointfs;
}
然后新建一幅与矩形区域相同大小的图像:
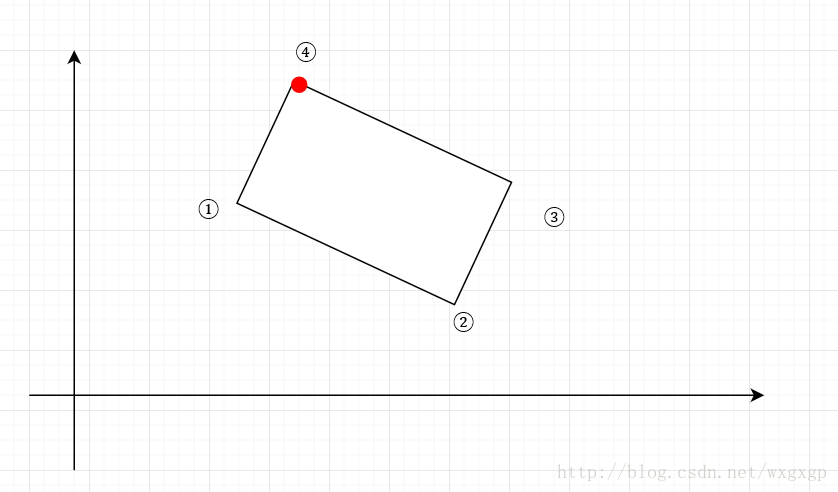
Image<Bgr, byte> newImg = new Image<Bgr, byte>(new Size((int)rect.Size.Width, (int)rect.Size.Height));因为要复制原始图像区域内的像素,所以并不是对原始图像旋转,而是对newImg内的点与原始图像内的点对应起来,进行一个映射。

如上图所示,绿色矩形为newImg,蓝色矩形为身份证号区域,首先将将绿色矩形的坐标平移到红色虚线矩形处,然后再旋转虚线矩形的坐标,即完成了坐标映射。
设newImg的坐标为(x0,y0),img(原始图像)的坐标为(x,y)平移的偏移量为(Δx,Δy),旋转角度为angle,则(x0,y0)处的像素值可以表示为:
(x0,y0).Color = rote(angle)[(x0+Δx,y0+Δy)].Color
具体代码如下:
public static Image<Bgr,byte> Rote(Image<Bgr,byte>img, RotatedRect rect)
{
PointF center = new PointF();
PointF[] pointfs = RectCode(rect);
if(rect.Angle < 0)
{
center = pointfs[0];
}
if(rect.Angle >= 0)
{
center = pointfs[3];
}
Image<Bgr, byte> output = new Image<Bgr, byte>(new Size((int)rect.Size.Width, (int)rect.Size.Height));
int w = (int)rect.Size.Width;
int h = (int)rect.Size.Height;
for (int i = (int)center.X,m=0; i < w + (int)center.X; i++,m++)
{
for (int j = (int)center.Y, n = 0; j < h + (int)center.Y; j++,n++)
{
{
Point p = PointRotate(center, new PointF(i, j), -rect.Angle);
if (p.X >= img.Size.Width)
p.X = img.Size.Width - 1;
if (p.Y >= img.Size.Height )
p.Y = img.Size.Height - 1;
output[n, m] = img[p.Y, p.X];
}
}
}
if (Math.Abs(rect.Angle) > 45)
{
output = output.Rotate(180, new Bgr(Color.White));
}
return output;
}如此一来便提取出了各个区域的图像,下一步进行字符识别。
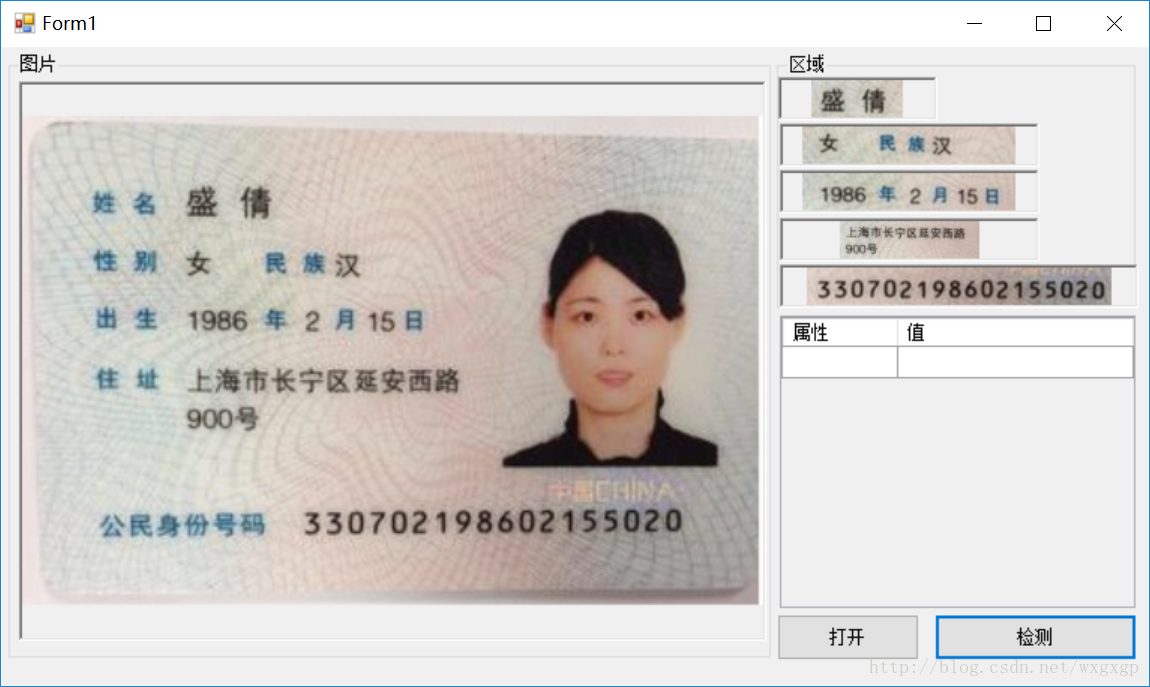
四、提取效果

附一: 获取各个区域的包围矩形的主要代码:
/// <summary>
/// 身份证号区域
/// </summary>
/// <param name="img"></param>
/// <returns></returns>
public static RotatedRect IdRotatedRect(Image<Bgr, byte> img)
{
Image<Bgr, byte> a = new Image<Bgr, byte>(img.Size);
VectorOfVectorOfPoint con = GetContours(BinImg(img));
Point[][] con1 = con.ToArrayOfArray();
PointF[][] con2 = Array.ConvertAll<Point[], PointF[]>(con1, new Converter<Point[], PointF[]>(PointToPointF));
for (int i = 0; i < con.Size; i++)
{
RotatedRect rrec = CvInvoke.MinAreaRect(con2[i]);
float w = rrec.Size.Width;
float h = rrec.Size.Height;
if (w / h > 6 && w / h < 10 && h > 20)
{
PointF[] pointfs = rrec.GetVertices();
for (int j = 0; j < pointfs.Length; j++)
{
CvInvoke.Line(a, new Point((int)pointfs[j].X, (int)pointfs[j].Y), new Point((int)pointfs[(j + 1) % 4].X, (int)pointfs[(j + 1) % 4].Y), new MCvScalar(0, 0, 255, 255), 4);
}
return rrec;
}
}
return new RotatedRect();
}
/// <summary>
/// 地址区域
/// </summary>
/// <param name="rr"></param>
/// <returns></returns>
public static RotatedRect AddressRotatedRect(RotatedRect rr)
{
float w = (float)((rr.Size.Width * 0.8));
float h = (float)(rr.Size.Height * 1.7);
float px = (float)(rr.Center.X - rr.Size.Height * 3.1);
float py = (float)(rr.Center.Y - rr.Size.Height * 2.4);
PointF center = new PointF(px,py);
RotatedRect rect = new RotatedRect(center,new SizeF(w,h),rr.Angle);
return rect;
}
/// <summary>
/// 年份区域
/// </summary>
/// <param name="rr"></param>
/// <returns></returns>
public static RotatedRect DateRotatedRect(RotatedRect rr)
{
float w = (float)(rr.Size.Width * 0.7);
float h = (float)(rr.Size.Height * 1);
float px = (float)(rr.Center.X - rr.Size.Height * 3.7);
float py = (float)(rr.Center.Y - rr.Size.Height * 4);
PointF center = new PointF(px, py);
RotatedRect rect = new RotatedRect(center, new SizeF(w, h), rr.Angle);
return rect;
}
/// <summary>
/// 性别区域
/// </summary>
/// <param name="rr"></param>
/// <returns></returns>
public static RotatedRect SexRotatedRect(RotatedRect rr)
{
float w = (float)(rr.Size.Width * 0.7);
float h = (float)(rr.Size.Height * 1);
float px = (float)(rr.Center.X - rr.Size.Height * 3.7);
float py = (float)(rr.Center.Y - rr.Size.Height * 5);
PointF center = new PointF(px, py);
RotatedRect rect = new RotatedRect(center, new SizeF(w, h), rr.Angle);
return rect;
}
/// <summary>
/// 姓名区域
/// </summary>
/// <param name="rr"></param>
/// <returns></returns>
public static RotatedRect NameRotatedRect(RotatedRect rr)
{
float w = (float)(rr.Size.Width * 0.3 );
float h = (float)(rr.Size.Height * 1 );
float px = (float)(rr.Center.X - rr.Size.Height * 5.1);
float py = (float)(rr.Center.Y - rr.Size.Height * 6.3);
PointF center = new PointF(px, py);
RotatedRect rect = new RotatedRect(center, new SizeF(w, h), rr.Angle);
return rect;
}
附二: 点旋转代码:
public static Point PointRotate(PointF center, PointF p1, double angle)
{
Point tmp = new Point();
double angleHude = angle * Math.PI / 180;/*角度变成弧度*/
double x1 = (p1.X - center.X) * Math.Cos(angleHude) + (p1.Y - center.Y) * Math.Sin(angleHude) + center.X;
double y1 = -(p1.X - center.X) * Math.Sin(angleHude) + (p1.Y - center.Y) * Math.Cos(angleHude) + center.Y;
tmp.X = (int)x1;
tmp.Y = (int)y1;
return tmp;
}附三: 判断点是否在多边形内
public static bool IsInside(Point inputponint,PointF[] pointfs)
{
GraphicsPath myGraphicsPath = new GraphicsPath();
Region myRegion = new Region();
myGraphicsPath.Reset();
myGraphicsPath.AddPolygon(pointfs);
myRegion.MakeEmpty();
myRegion.Union(myGraphicsPath);
return myRegion.IsVisible(inputponint);
}